うーん、いけそう。
だが、しかし wa.
WelcomToAtcoder_r0.py
N,M = map(int,input().split())
memo = [False]*N
wa = 0
for _ in range(M):
p,S = input().split()
p = int(p)-1
if not memo[p] and S == "WA":#AC未 get 問題で wa なら インクリメント
wa += 1
elif S == "AC":#AC なら memo を ture.AC は後で true の数を数えればいい。
memo[p] = True
ac = memo.count(True)
print("{} {}".format(ac,wa))
なぜ wa なのか分からなかったから、
テストケースを確認した。
愕然とした。
問題文には AC を初めて出すまでの WA の数とある。
前述の記述では一個も AC が無い場合、WA の数を無限に数えるのではないだろうか?
WelcomToAtcoder_r1.py
N,M = map(int,input().split())
memo = [False]*N
wa = [0]*N
for _ in range(M):
p,S = input().split()
p = int(p)-1
if not memo[p] and S == "WA":
wa[p] += 1
elif S == "AC":
memo[p] = True
WA = 0
AC = memo.count(True)
for i in range(N):
if memo[i]:#正解するまでの WA をカウント
WA += wa[i]
print("{} {}".format(AC,WA))
再チャレンジ、ちゃんと理解してるかな。
問題文を読んで頭に浮かんだのは
以下のエッジケース。
edge_case.py
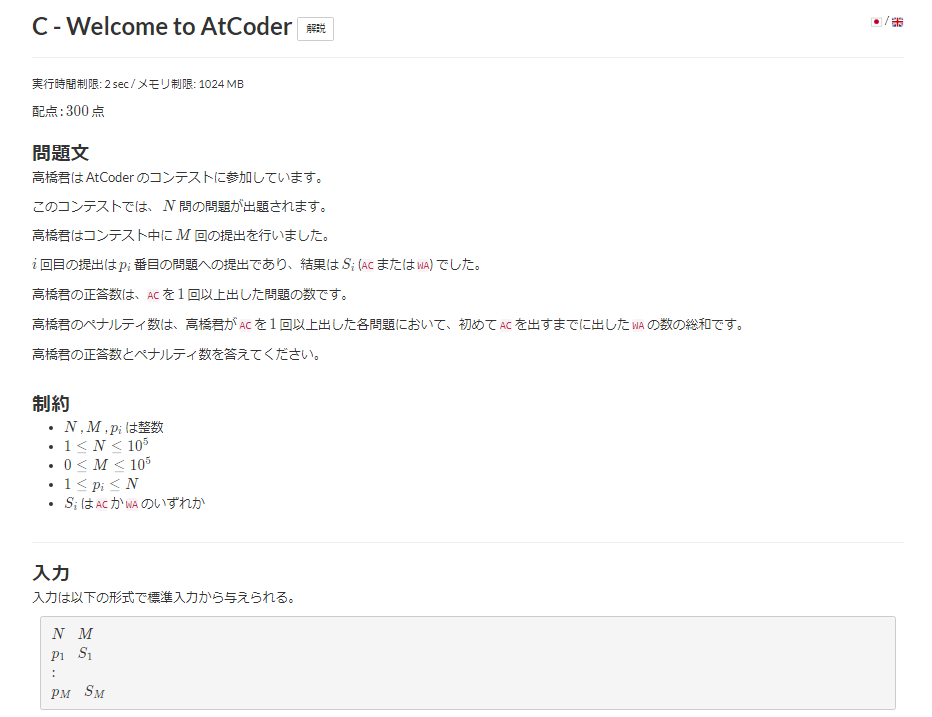
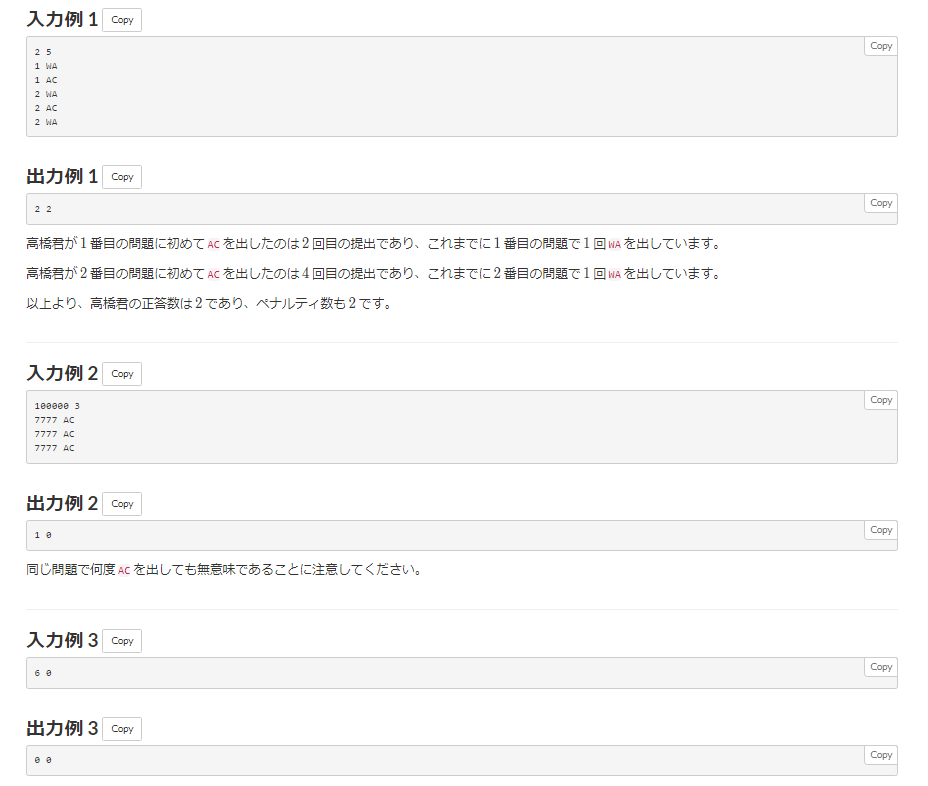
2 5
1 WA
1 AC
2 WA
2 WA
2 WA
AC が出るまでの WA カウントが正常にできるパターンと、
AC が出ずに WA が続くパターンの混在。
対策としては、各 N 問ずつ WA をメモするリストと、
AC を True / False でメモするリストを併用して管理する必要がある。
abc151c.py
N,M = map(int,input().split())
AC_memo = [False]*N #AC をメモ
WA_memo = [[] for _ in range(N)] #WA をメモ
for _ in range(M):
p,s = input().split()
p = int(p)
if not AC_memo[p-1] and s == "WA": #未AC かつ WA なら WA としてメモ
WA_memo[p-1].append("WA")
elif not AC_memo[p-1] and s == "AC": #未AC かつ AC なら AC としてメモ
AC_memo[p-1] = True
AC = AC_memo.count(True) #ACは簡単。True を数えるだけ
WA = 0
for i in range(N): #i番目の問題で WA 数をカウントしたい
if AC_memo[i] and len(WA_memo[i]) > 0:#条件として AC_memo[i] が True である必要がある
WA += len(WA_memo[i])
print(AC,WA)
よかった。書き方にはスマートさが足りないが
ポイントを突くことが出来て、無事 AC.