自己紹介
初めまして。
本誌を訪問頂き有難うございます。
私は半導体(FPGA/DCDC)の FAE(技術営業)を 12年やっている者です。
技術営業は、営業と一緒に製品の売り込み以外にも
技術サポート(製品に関する技術的な質問の対応)と不具合対応(デバイス不良)が業務です。
デバイス不良との名目でデバックに付き合わされることも多々あるので、
ソフト/ハード面の両方をサポートする、ほぼ何でも屋さんです。
そんな私が趣味で始めた python programming。
業務の FPGA では Verilog,VHDL でプログラム言語を扱っていたので
python は趣味の延長として楽しく触っていますが、開発屋さんでは無いので素人です。
ちょっと力試しに leetcode を始めてみました。
早速直面した壁
自慢ではありませんが、私は素人です。基礎がありません。
そんな私が leetcode に挑戦する場合、行動方針は
0からアルゴリズムを頭の中で組み立ててプログラムを書く!!
この一点突破のみです。
この行動方針には思考力を養うメリットがあるかもしれませんが
デメリットの方が多いように感じます。私が思うデメリットは以下です。
1.自分流で 0 から組み立てようとするので、とにかく時間が掛かる!
2.自分流はとにかく、無駄な記述が多い
3.記述が多くなるとミスが増える
4.脳がトップギアに入っていない場合、過去に解けた問題も解けない場合がある
つまり、処理時間が多く、そのアウトプットが安定しない。
全くいいことがありません。
基礎をしっかり学び、吸収した基本形をベースに問題に挑む事で
処理時間の短縮と Output の安定化を図った私なりのチャレンジをすることにしました。
本誌は、その記録です。
勿論、愛のある突っ込みは大歓迎です。
基礎の定義
今回は Leetcode:Explorer Binary Treeを基礎とします。
方針は基本形を覚えて動作を理解します。
例題を基礎と定義しているくらいですから、その動作イメージが全てに通じる考え方になるんだと思います。
探索の練習には、復習も兼ねて作った、以下の二分探索木をベースに話を進めていきます
(node 削除は割愛)。
# 二分探索木には関係ない記述ですが、
# 探索時に deque() を使うので予め記載
from collections import deque
# node の定義
class node:
def __init__(self,val,left=None,right=None):
self.val = val
self.left = left
self.right = right
class BinTree:
#self.root をベースにツリーを作る、初期値 None
def __init__(self):
self.root = None
def add(self,val):
#以下の def add_node を読み飛ばして、下部のコメントに GO!
def add_node(root,val):
if val < root.val:
if not root.left:
root.left = node(val)
else:
add_node(root.left,val)
if val > root.val:
if not root.right:
root.right = node(val)
else:
add_node(root.right,val)
#def add() で最初に実行するプログラム。
#最初に self.root が None か否かを確認し
#None であれば node を call して val を代入
if not self.root:
self.root = node(val)
#not None であれば add_node を call
else:
add_node(self.root,val)
#### Tree_image#####
# 4 #
# / \ #
# 2 6 #
# / \ / #
# 1 3 5 #
###################
T = BinTree() #self.root の作成
T.add(4)
T.add(2)
T.add(3)
T.add(1)
T.add(6)
T.add(5)
簡単に補足すると、二分探索木として成立させるためには
def add() の中に埋め込んだ def add_node() の記述がミソだと思います。
ノードとしての分岐の度に、分岐元の value より大きいのか、小さいかを
判断する必要があるからです。
探索方法
leetcode によると探索方法は DFS: Pre-order/ In-order/ Post-order, BFS が挙げられています。
下図は、それぞれのアプローチのイメージです。各ノードに振られた番号は探索の順番です。
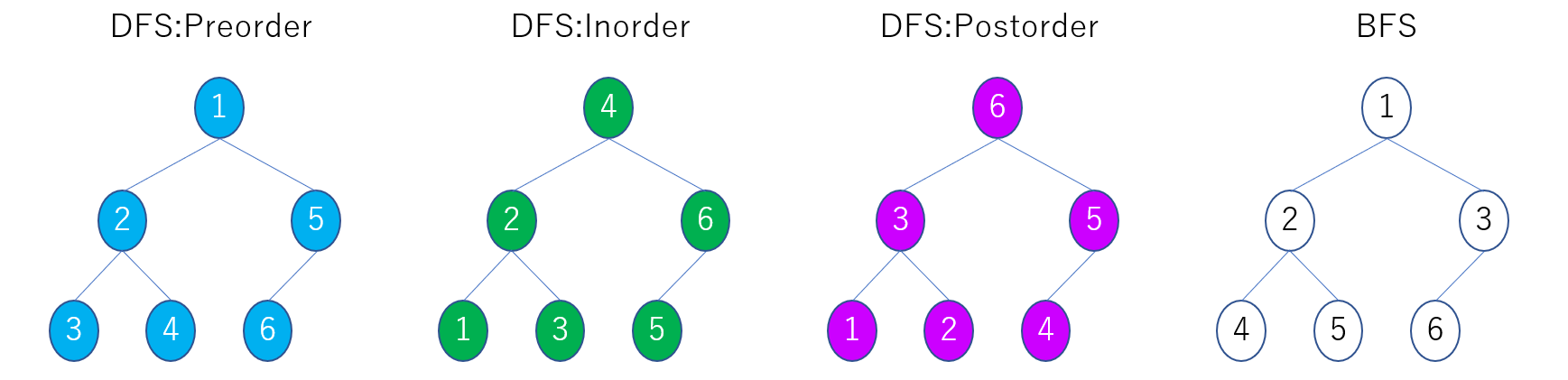
この図を見ただけでプログラムを思い描くのは至難です。
本誌では例題から基本形を理解し、覚えてしまいます。
その基本形を組み替えて応用できないか練習する方針で進めます。
例題1 DFS:Preorder/Inorder/Postorder
二分探索木を探索し、各ノードで値を返してください。 但し、探索アプローチは Preorder/Inorder/Postorder の 3 つを使う事。
Input: root = [4,2,6,1,3,5]
Output:4 #-----Tree_image---#
2 # 4 #
1 # / \ #
3 # 2 6 #
6 # / \ / #
5 # 1 3 5 #
#------------------#
【制約】
・ツリーの要素は 0 ~ 100 で構成
・-100 <= node.val <= 100
解説
これは例題なので分からなくて OK です。
以下の流れで行きましょう。
1.いきなり回答を読む
2.動作をイメージする
3.別途用意した GIF で答え合わせ
では早速、回答の登場です。
Preorder/Inorder/Postorder の 3 パターンのアプローチを学習します。
def DFS(self):
def pre_order(node):
print(node.val)
if node.left:pre_order(node.left)
if node.right:pre_order(node.right)
def in_order(node):
if node.left: in_order(node.left)
print(node.val)
if node.right: in_order(node.right)
def post_order(node):
if node.left: post_order(node.left)
if node.right: post_order(node.right)
print(node.val)
#-----------------------#
#--select DFS approach--#
#-----------------------#
#1 preorder
return pre_order(self.root)
#2 inorder
#return in_order(self.root)
#3 postorder
#return post_order(self.root)
ご覧のとおり,Preorder/Inorder/Postorder の記述に差分は殆どないです。
読みながらイメージを作ってみましょう、間違っても良いと思います。
作ったイメージに漏れが無いか確認していきましょう。
以下の GIF はクリックすると拡大するので分かり易くなります。



print() で全て表示が出来たら終わりではなく、
最後まで処理を追いかけて完結することを確認してみると理解が深まります。
念のため別アプローチも検討してみましたがスマートな記述は他にあると思います。
今はこのレベルでの共有で申し訳ないです。
# Preorder
def DFS(self):
buff = [self.root]
while buff:
nums = buff.pop()
print(nums.val)
if nums.right: buff.append(nums.right)
if nums.left: buff.append(nums.left)
"""
# Inorder
def DFS(self):
B0 = deque([self.root])
B1 = []
root = B0.popleft()
while root or B1:
while root:
B1.append(root)
root = root.left
root = B1.pop()
print(root.val)
root = root.right
"""
"""
# Postorder
def DFS(self):
buff,ans=deque([self.root]),deque([])
while buff:
nums = buff.pop()
ans.appendleft(nums.val)
if nums.left:buff.append(nums.left)
if nums.right:buff.append(nums.right)
for i in range(len(ans)):
print(ans[i])
"""
準備が出来たので Leetcode にチャレンジします。
演習1 Binary Tree Preorder/Inorder/Postorder
二分探索木を探索し、各ノードをリストして返してください。 但し、探索アプローチは Preorder/Inorder/Postorder の 3 つを使う事。
Input: root = [4,2,6,1,3,5]
Output: [4,2,1,3,6,5]
【制約】
・ツリーの要素は 0 ~ 100 で構成
・-100 <= node.val <= 100
解説
例題1 で解いた(or 覚えた)基本形で何とかしましょう。
しかし、例題の丸コピーでは演習を解くのは難しいと思います。
再帰処理で解く場合、関数の冒頭から入って、
return で再度関数の冒頭に戻る場合、出力用の [ ] の定義が邪魔になります。
例えば、ans = [ ] と定義した場合、再帰的に冒頭に戻ると
必ず ans = [ ] と初期化してしまうので、計算値を蓄積できません。
今の自分では対応策が見当たらなかったので、
今回は def の中に def を埋め込んで検討してみました。
def DFS(self):
ans = []
def preorder(node,ans):
ans.append(node.val)
if node.left: preorder(node.left,ans)
if node.right: preorder(node.right,ans)
return ans
return preorder(self.root,ans)
前述にあるように DFS の中に preorder を用意して、
preorder で再帰処理させています。
必ず、node.val を格納した ans を次の階層に持っていくために、
preorder(node.left,ans) としています。
御存知の方も多いと思いますが、実はこの ans は省略できます。
ほとんど変わりませんが、以下の記述でも同様の output が得られます。
def DFS(self):
ans = []
def preorder(node):
ans.append(node.val)
if node.left: preorder(node.left)
if node.right: preorder(node.right)
return ans
def inorder(node):
if node.left: preorder(node.left)
ans.append(node.val)
if node.right: preorder(node.right)
return ans
def postorder(node):
if node.left: preorder(node.left)
if node.right: preorder(node.right)
ans.append(node.val)
return ans
#-----------------------#
#--select DFS approach--#
#-----------------------#
#1 preorder
return pre_order(self.root)
#2 inorder
#return in_order(self.root)
#3 postorder
#return post_order(self.root)
もう一つのポイントは return です。
node.val を追加した ans を呼び出し元に通知しないと、
全ての要素を拾って最終 output が出来ません。
念のため私の説明に嘘が無いか、GIF を作って確認してみました(笑)。

Inorder/Postorder も基本は同じなので GIF は不要だと思いますが、リクエストがあれば検討いたします。
例題2 BFS
二分探索木を探索し、各ノードを BFS で探索して値を返してください。
Input: root = [4,2,6,1,3,5]
Output:4 #-----Tree_image---#
2 # 4 #
6 # / \ #
1 # 2 6 #
3 # / \ / #
5 # 1 3 5 #
#------------------#
【制約】
・ツリーの要素は 0 ~ 100 で構成
・-100 <= node.val <= 100
解説
例題1 と同じ問題で申し訳ないです。
DFS と BFS を分けたのは基本アプローチが全く違うため、
混乱を避けるために分けました。
まずは、BFS のイメージを共有致します。

このイメージから、各層毎にデータをまとめてバッファすることで BFS を実現していることが分かります。
その実現方法ですが、こちらです。
def BFS(self):
q = [self.root]
def left2right(q):
laylength = len(q)
for _ in range(laylength):
nums = q.pop(0)
print(nums.val)
if nums.left:q.append(nums.left)
if nums.right:q.append(nums.right)
if laylength > 0:left2right(q)
return left2right(q)
コードの通りではあるのですが、
取り出した nums.val に含まれる nums.left / nums.right を q にバッファします。
上記の作業をlaylength(=len(q))回、繰り返すので、
結果的に同一階層のデータをまとめて q にバッファすることが出来ます。
勿論、q には他の層のデータが混ざる時もありますが、
for 分は laylength 回しか for を回さないので、
他の階層のデータを余分に取り出すようなマネはしません。

演習2 Binary Tree Level Order Traversal
二分探索木を探索し、各層でリストしてください。
Input: root = [4,2,6,1,3,5]
Output:[ #-----Tree_image---#
[4], # 4 #
[2,6], # / \ #
[1,3,5], # 2 6 #
] # / \ / #
# 1 3 5 #
#------------------#
解説
前述の例題では、すべての要素を q にバッファしますが、
各層毎に要素を根こそぎバッファして output しているので BFS が成立していました。
たとえばですが、for で回す処理を 1 階層目、2 階層目、3階層目..etc とナンバリング出来れば、
各層ごとに append() でききるので問題が解決できるのではないでしょうか。
そのアイディアを形にしたのが、こちらです。
def BFS(self):
q = deque([self.root])
ans = []
level = 0
def helper(q,level):
ans.append([])
laylength = len(q)
for _ in range(laylength):
nums = q.popleft()
ans[level].append(nums.val)
if nums.left:q.append(nums.left)
if nums.right:q.append(nums.right)
if len(q) > 0:helper(q,level+1)
return ans
return helper(q,level)
# def BFS(self):
# q = deque([self.root])
# level = 0
# ans = []
# while q:
# ans.append([])
# laylength = len(q)
# for _ in range(laylength):
# nums = q.popleft()
# ans[level].append(nums.val)
# if nums.left:q.append(nums.left)
# if nums.right:q.append(nums.right)
# level += 1
# return ans
コメントアウトで別アプローチを載せましたが、個人的には再帰処理じゃないほうが、
この件に関してはシンプルに書ける気がしています。
上記以外にもアプローチはあります。
DFS version を試してみました。
def DFS(self):
ans = []
level = 0
def pre_order(node,level):
if len(ans)==level:
ans.append([])
ans[level].append(node.val)
if node.left:pre_order(node.left,level+1)
if node.right:pre_order(node.right,level+1)
return ans
def in_order(node,level):
if len(ans)==level:
ans.append([])
if node.left: in_order(node.left,level+1)
ans[level].append(node.val)
if node.right: in_order(node.right,level+1)
return ans
def post_order(node,level):
if len(ans)==level:
ans.append([])
if node.left: post_order(node.left,level+1)
if node.right: post_order(node.right,level+1)
ans[level].append(node.val)
return ans
#-----------------------#
#--select DFS approach--#
#-----------------------#
#1 preorder
return pre_order(self.root,level)
#2 inorder
#return in_order(self.root,level)
#3 postorder
#return post_order(self.root,level)
BFS を解いた後だと、どうしても以下のように解きたがってしまいます。
def DFS(self):
q = [self.root]
ans = []
level = 0
def preorder(q,level):
if len(ans)==level:
ans.append([])
nums = q.pop(0)
ans[level].append(nums.val)
if nums.left:
q.append(nums.left)
preorder(q,level+1)
if nums.right:
q.append(nums.right)
preorder(q,level+1)
return ans
return preorder(q,level)
このコードは BFS でイメージしたような"バッファ"を一旦頭から
切り離して考えられなかった結果です。
DFS はデータ単体で考えても勝手にツリー全体を探索してくれますので、
バッファのイメージを捨てて使っても問題ないのです、良い勉強になりました。
演習3 Maximum Depth of Binary Tree
与えられた Tree の深さの最大値を求めてください。
Input: root = [4,2,6,1,3,5]
Output:3 #-----Tree_image---#
# 4 #
# / \ #
# 2 6 #
# / \ / #
# 1 3 5 #
#------------------#
【制約】
・ツリーの要素は 0 ~ 10^4 で構成
・-100 <= node.val <= 100
解説
有識者の回答は以下のようになっていました。
def maxDepth(self, root: TreeNode) -> int:
if not root:
return 0
else:
left = self.maxDepth(root.left)+1
right = self.maxDepth(root.right)+1
return max(left,right)
return max(self.maxDepth(root.left),self.maxDepth(root.right))+1
leatcode は上記で通りますが、
ローカルで色々試すときは以下のように少し変更してます。
def maxDepth(self):
def helper(node):
if not root:
return 0
else:
left = helper(root.left)+1
right = helper(root.right)+1
return max(left,right)
return max(helper(self.root.left),helper(self.root.right))+1
Point
leaf or none node で leaf まで辿り着けなかったとしても、その全てをカウントします。 欲しいものは最大値なので max() を使って答えを探す返すアプローチで全く問題ない

他の問題もこなしながら筆者のイメージと理解がまとまってきたので
再チャレンジしたところ以下の記述で accept されました。
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if not root:return 0
L = self.maxDepth(root.left) + 1
R = self.maxDepth(root.right) + 1
return max(L,R)
現状の理解の範囲内で恐縮ですが、ポイントを抑えることで
記述を最適化することができました。
しかし、記述の最適化が出来ても、処理時間、メモリの占有領域の
観点で考えると、まだまだ先がありそうです。
上記に関してはどうやって突き詰めればよいのか分からないので
有識者の回答を理解、吸収することにしました。
class Solution:
def __init__(self):
self.ans = 0
def maxDepth(self, root: TreeNode) -> int:
def helper(node,cnt):
if not node:return
if not node.left and not node.right:
self.ans = max(self.ans,cnt)
helper(node.left,cnt+1)
helper(node.right,cnt+1)
helper(root,1)
return self.ans
考え方は斬新で、冒頭に self.ans を置いて
maxDepth() で self.ans をドンドン更新していくアプローチです。

演習4 にあるように、最初に not node.right and not node.left となったノード階層が最小階層という
考え方をヒントに別解を思いつきました。
BFS で探索を行い、バッファした q の値が無くなった時に今までカウントした階層を返せば最下層と同等ですよね?
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if not root: return 0
def helper(node,cnt):
q = [node]
while q:
cnt += 1
length = len(q)
for _ in range(length):
nums = q.pop(0)
if nums.left:q.append(nums.left)
if nums.right:q.append(nums.right)
return cnt
return helper(root,0)
演習4 Minimum Depth of Binary Tree
与えられた二分探索木の最小の深さを求めてください。
# Example 1
Input: root = [3,9,20,null,null,15,7]
Output: 2
# Example 2:
Input: root = [2,null,3,null,4,null,5,null,6]
Output: 5
[制限]
・Tree を構成する node 数は 0 ~ 10^5
・-1000 <= node.val <= 1000
解説
Maximum Depth of Binary Tree を流用して何とかならないか検討してみました。
if node.left もしくは if node.right で条件を付けることで
None node はカウントせずに、必要な物だけを数えて output してくれる事を期待しました。
class Solution:
def minDepth(self, root: TreeNode) -> int:
self.L,self.R = 0,0
def helper(node):
if not node:return 0
else:
if node.left: self.L = helper(node.left)+1
if node.right:self.R = helper(node.right)+1
return min(self.L,self.R)
return helper(root) +1
Run code は通りましたが、submit は通りませんでした。
そうなんです。このコードには大きな欠点があります。
まずは以下のツリー構成をご覧ください。
0
\
1
\
2
ご覧いただくと分かるように self.L は値の更新が一切ないので
self.R の更新が終わった後に、最終的に min(self.L,self.R) としてしまうと
self.L の初期値 0 の方が小さくなるので、output は 0 + 1 で 1 になります。
本当は 3 が欲しいのに。。残念。
POINT1
再帰処理のループ内に return 0 を組み込むと ツリーの最深部以外の部分で 0 が返り、最小値となってしまう可能性があります。 よって、最小値をカウントする問題の場合は、必ずカウントした値だけを返します。
POINT2
左部分木、右部分木と分けて最後に min() を使って回答を求めるアプローチは この最小値を求める問題には厳禁です。途中で切れている物は最小値として採用できますが、 前述にあるように全く要素が無い場合、初期値が return されるので悪手になります。
そもそも初期値を 0 としなければ良いのですが、
書き方を間違えると、設定した初期値に探索結果を加算することになります。
例えばですがリファレンスとして M を無限大とし、
M と比較して小さい方を常に比較して更新していくアプローチが良いと思います。`
class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root:return 0
if not root.left and not root.right:return 1
#self.M = float("inf") #<= ここに M を置いても OK
def helper(node,cnt):
M = float("inf")
if not node.left and not node.right:return cnt
if node.left: M = min(M,helper(node.left,cnt+1))
if node.right:M = min(M,helper(node.right,cnt+1))
return M
return helper(root,1)
念のため GiF を使ってイメージの確認をします。

以上のアプローチはご理解いただいているように全探索を行い M を最小値に更新しています。
全てを探索せずに最小値を求めるアプローチを発見いたしました。
class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root:return 0
cnt = 0
q=[root]
while q:
cnt += 1
length = len(q)
for _ in range(length):
nums = q.pop(0)
if not nums.left and not nums.right:
return cnt
else:
if nums.left: q.append(nums.left)
if nums.right:q.append(nums.right)
return 0
上記の記述で素晴らしいのは BFS でアプローチして not root.left and not root.right に
該当した深さを最初に return した値が最小値であるという考え方です。
処理時間も 660ms :再帰処理から 470ms :BFS へ改善することができました。
勉強になりました m(_ _)m
演習5 Symmetric Tree
ツリーが対象か否かを確認してください。
# For example, this binary tree [1,2,2,3,4,4,3] is symmetric:
1
/ \
2 2
/ \ / \
3 4 4 3
# => return True
# But the following [1,2,2,null,3,null,3] is not:
1
/ \
2 2
\ \
3 3
# => return False
解説
時間をかけて何度もイメージしてみたのですが
以下の要点を抑える記述が必要である印象です。
POINT0.ノードが無ければ対称なので True
POINT1.中身は置いておき、シルエットが対象であるかを確認
POINT2.左右のノードの値が同一であるかを確認
POINT3.左右、それぞれのノードの子が対象か確認
def Symetric(root):
if not root:return True # POINT 0
def helper(t1,t2):
if not t1 and not t2:return True # POINT 1
if not t1 or not t2:return False# POINT 1
return (t1.val == t2.val) and \
helper(t1.left,t2.right) and \
helper(t1.right,t2.left) # POINT 3
return helper(root.left,root.right)
POINT0補足
与えられた Tree が [ ] だった場合、何もない状態、つまり"無"が対象なので True が返ります。
POINT1補足
t1,t2 の両者が None であれば対象なので True。
t1,t2 のいずれかが None であれば非対称なので Flase。
POINT2補足
POINT0 - 2 をパスしてきた場合、return に降りる頃には
t1,t2 are not None の状況であることは明白です。
POINT3補足
t1,t2 には、それぞれ left ,right のノードが存在しているか確認、存在していれば
node.val が同一であるかを確認するアクションが必要
helper(t1.left,t2.right) and helper(t1.right,t2.left) の再帰処理でシルエットと値の整合を取る
前述の POINT をイメージしながらコードを読んでみると以下にある GIF とイメージが同期できると思います。

蛇足かもしれませんが、検証用に作った環境は以下になりますので
自分でも試したい方は参考にしていただければ幸いです。
class node:
def __init__(self,val,left=None,right=None):
self.val = val
self.left = left
self.right = right
def Symmetric(node):
if not root:return True
def helper(t1,t2):
if not t1 and not t2:return True
if not t1 or not t2:return False
return (t1.val == t2.val) and \
(helper(t1.left,t2.right)) and\
(helper(t2.left,t1.right))
return helper(node.left,node.right)
##Tree_image####
# 0
# / \
# 1 1
# / \ / \
# 2 3 3 2
################
root = node(0)
root.left = node(1)
root.right = node(1)
root.left.left = node(2)
root.left.right = node(3)
root.right.left = node(3)
root.right.right = node(2)
print(Symmetric(root))
因みに類題にはなりますが、2 つのツリーを比較して同一か否かを
確認することも同じ考え方で解けます。
100.Same Tree
Given the roots of two binary trees p and q, write a function to check if they are the same or not.
Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
if not p and not q : return True
if not p or not q : return False
return (p.val == q.val) and self.isSameTree(p.right,q.right) and self.isSameTree(p.left,q.left)
演習6 Path sum
与えられたツリーで、root <=> leaf 間の合計が、sum と一致する場合、 True を、一致しなければ False を返してください。
# Example:
# Given the below binary tree and sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1
解説
いつぞやに勉強した部分和の記述を思い出しながら
今回の問題に当てはまらないか検討しました。
class Solution:
def hasPathSum(self, root: TreeNode, sum: int) -> bool:
if not root:return False
if not root.left and not root.right:
return sum-root.val == 0
if self.hasPathSum(root.left,sum-root.val):
return True
if self.hasPathSum(root.right,sum-root.val):
return True
return False
前述の記述については曖昧な理解であることは否めないので
GIF を作って追いかけてみることにしました。
sum = 7 として True のケースを 2つ検証してみました。


DFS の動きそのものを改めて確認することが出来ました。
if 分があってもそこは変わらないようです。
動作を追いかけてて面白いと感じたのは以下の 2 点でした。
POINT 1.
if の条件文に再帰処理を組み込むのであれば、冒頭にあるように
not root を if 分の条件文として組み込んで Return False とします。
これにより leaf に辿り着く前の none node を false で返すことができます。
もし if の条件文が、これにより False なのであれば、その if 分は pass し、次の if 分に移行します。
次の if 分は node.right を探索するものになっているので、DFS の所以がここにあります。
POINT 2.
leaf に辿り着いたのであれば
return sum-root.val == 0 とすることで True or False を返します。
if 条件文が True なのであれば return True となりますし、
False なのであれば次の if 分に移行します。
それでもダメであれば DFS で全探索しても合計値が要件を満たさないことになるので
False を返す構成になっています。
しかし、もっと素晴らしい回答を発見しました。微力ながら筆者の理解を
コメントしました。素晴らしいコードにコメントなんて恐れ多いですが。。
def PathSum(node,sum):
#before reaching the leaf, if it face None node. it is false.
if not node:return False
#subtract node.val from sum every time, we go through the node.
sum -= node.val
# if we reach the leaf, let us check whether path sum equals sum.
if not node.left and not node.right:
return sum == 0
#First time,we subtract node.val from sum
#after that,let us use recursive approach to research the rest node.
return PathSum(node.left,sum) or PathSum(node.right,sum)
演習 7 Validate Binary Search Tree
与えられた木が二分探索木かどうかを確認してください。
二分探索木の判断は以下の項目に着目して判断してください。
・ノードの値 > 左ノードの値
・ノードの値 < 右ノードの値
・左/右ノードの部分木も二分探索木であること
# Example 1:
Input: root = [2,1,3]
Output: true
# Example 2:
Input: root = [5,1,4,null,null,3,6]
Output: false
# Explanation: The root node's value is 5 but its right child's value is 4.
解説
inorder でアプローチしてみました。
二分探索木であるかは、部分木の値を記憶しておき、
大小を比較して判別しています。
class Solution:
def isValidBST(self, root: TreeNode) -> bool:
def helper(root):
if not root:return True
if not helper(root.left):
return False
if self.prev >= root.val:
return False
self.prev = root.val
return helper(root.right)
self.prev = -float("inf")
return helper(root)
前述のコードだけでは理解が難しいと思いますので、
簡単な tree を用意して動きを確認したいと思います。

BST を二分探索した場合、inorder で探索すると left:leaf to root , right:root to leaf で
それぞれ right or left leaf.val Vs root.val の関係は以下のようになります。
POINT1
左部分木の探索の場合、leaf => root の方向で戻りますが、その時は leaf.val < root.val が成立
右部分木の探索の場合、root => leaf の方向で進みますが、その時は root.val < leaf.val が成立
また def inorder() の最後をなぜ return で締めているのか理由が分からなかったので、
別のケースを作って検証してみました。

POINT2
def inorder() の最終行で、def inorder() そのものを False or True と明示しないと再帰処理が成立しない
念のため False の条件も作って検証しました。
右部分木に False となる要素を仕込んでおきましたので、
以下の GIF では左部分木の探索が終わって右部分木に向かい始めるところから start しています。

部分木に関しては left_leaf.val < node.val and node.val < right_leaf.val は必須なのですが、
root.val より小さいものが右部分木に潜んでいるケースは二分探索木とは言えないのでチェックすべきポイントです。
GIF にあるようにしっかりチェックして判定できている事が分かります。
演習 8 Count Unival Subtrees
二分探索木をプレゼントするので、uni-value 部分木の数を教えてください。
uni-value 部分木は同じ値をもつ部分木を指します。
# Example 1:
Input: root = [5,1,5,5,5,null,5]
Output: 4
# Example 2:
Input: root = []
Output: 0
# Example 3:
Input: root = [5,5,5,5,5,null,5]
Output: 6
制限:
与えられるツリーのノード数は 0 ~ 1000.
-1000 <= Node.val <= 1000
解説
uni-value subtree の解釈について一旦整理したいと思います。
筆者の最初の理解では、カウントしたノードの値が全て同一であると思っていました。
しかし、実際は違うようです。
POINT 1.
子を持つ中間ノードは、左右の子と中間ノードの値が同じでないと
uni-value subtree としてカウントは出来ない。
POINT 2.
子を持たないノードの場合は、node.val の一つだけで uni-value subtree か否かを判断します。
検討する要素が 1 つしかないので uni-value subtree としてカウントします。
POINT 3.
subtree 内の値が同一であるものをカウントするので、
カウントした subtree 間で値が異なっていても同じでも、どちらでも良い。
これを前提に Example で挙げられている回答例を GIF で追いかけてみます。
class Solution:
def countUnivalSubtrees(self, root: TreeNode) -> int:
self.count = 0
self.is_valid_part(root,0)
return self.count
def is_valid_part(self,node,val):
if not node:
return True
if not all([self.is_valid_part(node.left,node.val),self.is_valid_part(node.right,node.val)]):
return False
self.count += 1
return node.val == val
蛇足になるかもしれませんが
以下の検証例を参考に挙げておきます。
### Tree_image###
# 5 #
# / \ #
# 1 5 #
# / \ \ #
# 5 5 5 #
# Example 1:
Input: root = [5,1,5,5,5,null,5]
Output: 4
### Tree_image###
# 5 #
# / \ #
# 1 5 #
# / \ \ #
# 5 3 5 #
# Example 2:
Input: root = [5,1,5,5,3,null,5]
Output: 4
演習9 Construct Binary Tree from Inorder and Postorder Traversal
inorder/postordr のリストを使って二分探索を作成してください。
Note:
node.val にダブりはナシです。
inorder = [9,3,15,20,7]
postorder = [9,15,7,20,3]
Return the following binary tree:
3
/ \
9 20
/ \
15 7
解説
List としてある inorder , postorder の情報をヒントに
Binary tree を作る問題です。
inorder は leaf から回っているところもあり、
これだけでは何が何だかサッパリわかりません。
しかし、postorder が解決の糸口になります。
それは必ず最終項が必ず root.val である点です。
inorder.index() を使って root が居る位置より右側は右部分木
左側は左部分木ということになります。
これらを再帰処理でうまく Tree 作成に持っていければ良いのです。
取り急ぎ回答と、
それを評価確認する環境を用意し直しました。
class node:
def __init__(self,val,left=None,right=None):
self.val = val
self.left = left
self.right =right
class solution:
def __init__(self):
self.root = None
def buildTree(self,inorder,postorder):
def helper(inorder,postorder):
if not inorder:
return None
cur_val = postorder.pop()
idx = inorder.index(cur_val)
right = helper(inorder[idx+1:],postorder)
left = helper(inorder[:idx] ,postorder)
return node(cur_val,left,right)
self.root = helper(inorder,postorder)
def show(self):
def helper(node):
print(node.val)
if node.left:helper(node.left)
if node.right:helper(node.right)
return helper(self.root)
post = [9,15,7,20,3]
inor = [9,3,15,20,7]
Tree = solution()
Tree.buildTree(inor,post)
Tree.show()
例のごとく GIF で追いかけたいと思います。

頭の中で何回もイメージして是非自分のモノにしていきたいですね。
演習10 Construct Binary Tree from Preorder and Inorder Traversal
preorder/inordr のリストを使って二分探索を作成してください。
Note:
node.val にダブりはナシです。
# For example, given
preorder = [3,9,20,15,7]
inorder = [9,3,15,20,7]
# Return the following binary tree:
3
/ \
9 20
/ \
15 7
解説
演習 9 と基本的には同じです。
今回は postorder の代わりに preorder を使っているので
pop する向きを変えるだけです。
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
if not inorder:
return None
cur_val = preorder.pop(0)
idx = inorder.index(cur_val)
left = self.buildTree(preorder,inorder[:idx])
right = self.buildTree(preorder,inorder[idx+1:])
return TreeNode(cur_val,left,right)
演習11 Populating Next Right Pointers in Each Node
同一階層に全て葉があり、すべての親には子が 2 人いる完全二分木を差し上げます。
完全二分木には以下の定義があります。
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
next には、同一層の、そのノードの右側を指定しています。
もし、右側にノードが無い場合は、NULL が入ります。
初期値として全てのノードの next には NULL が格納されています。
Input: root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]
# Explanation:
# Given the above perfect binary tree (Figure A),
# your function should populate each next pointer to point to its next right node,
# just like in Figure B. The serialized output is in level order as connected by the next pointers,
# with '#' signifying the end of each level.
解説
class Solution:
def connect(self, root: 'Node') -> 'Node':
if not root:
return root
leftmost = root
while leftmost.left:
head = leftmost
while head:
head.left.next = head.right
if head.next:
head.right.next = head.next.left
head = head.next
leftmost = leftmost.left
return root
演習12 Populating Next Right Pointers in Each Node II
二分木を差し上げます。ノードの構成は以下のようになっています。
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
ノードの next に右側に隣接するノードをつなげてください。
もし、ノードの右側に何もなかった場合は、Null を格納してください。
全ノードは初期値として next に Null を格納しております。
解説
class Solution:
def connect(self, root: 'Node') -> 'Node':
def conn(node, d, dmap):
if not node:return
if d in dmap:
n = dmap[d]
n.next = node
dmap[d] = node
conn(node.left, d+1, dmap)
conn(node.right, d+1, dmap)
conn(root, 0, {})
return root
まずは軽く動きを追ってみます。

しかし、これだけでは有用性が分からないので Tree を大きくします。

左側のノードを root から leaf に至るまで、
順番に dmap = { } へ格納しています。
そのときに d を使ってナンバリングしています。
これにより右側の探索に向かった際に dmap から同一階層のノードを呼び出すことで
隣接するノードを手元に揃える事ができます。あとは .next で接続するだけです。
演習13 Lowest Common Ancestor of a Binary Tree
二分木をプレゼントします。
その中から、2 つの Lowest common ancestor(LCA)を Tree から探してください。
# Example 1:
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
# Explanation: The LCA of nodes 5 and 1 is 3.
# Example 2:
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
# Explanation: The LCA of nodes 5 and 4 is 5,
# since a node can be a descendant of itself according to the LCA definition.
# Example 3:
Input: root = [1,2], p = 1, q = 2
Output: 1
LCA とは 指定された2つのノードを左右で leaf で挟まれているノードで最も root に近い個所みたいです。
解説
leaf までちゃんと降りていき、
leaf が p or q に該当しているのか確認する。
もしくは、すでに p or q を見つけていた場合、
その node を return することが出来れば占めたものです。
class Solution:
def lowestCommonAncestor(self, root, p, q):
if not root:
return None
left = self.lowestCommonAncestor(root.left,p,q)
right= self.lowestCommonAncestor(root.right,p,q)
if (root in [p,q]) or (left and right):
return root
else:
return left or right
演習14 Serialize and Deserialize Binary Tree
Tree を差し上げるので Serialize してください。つまりツリーから値を抜き出してリストしてください。
DeSerialize は、取り出したデータからツリーを作ってつくってください。
# Example 1:
Input: root = [1,2,3,null,null,4,5]
Output: [1,2,3,null,null,4,5]
# Example 2:
Input: root = []
Output: []
# Example 3:
Input: root = [1]
Output: [1]
# Example 4:
Input: root = [1,2]
Output: [1,2]
解説
問題文で気になったのは None の存在です。
とりあえず、文字として全てを serialize を実行します。
def T2S(root):
def helper(root,string):
if not root:
string += "None,"
return string
else:
string += str(root.val)+ ","
string = helper(root.left,string)
string = helper(root.right,string)
return string
return helper(root,"")
これは leaf の left / right に対しても None であることを含めてキッチリ抜き取ることができます。
ここまで情報を揃えておかないと、次に Tree に起こし直すときに不便だと思います。
次に Tree に起こし直す作業です。
これは今まで学習した内容で何とか切り抜けられると思います。
def S2T(data):
datalist = data.split(",")
def helper(data):
if data[0] == "None":
data.pop(0)
return None
nums = data.pop(0)
root = node(nums)
root.left = helper(data)
root.right= helper(data)
return root
return helper(datalist)
image としては inorder で左端の leaf の None まで
代入が完了したら、root に向かって戻りながら
Tree を構成していく算段になっています。
検証した環境も併せてメモで残しておきます。
class node:
def __init__(self,val,left=None,right=None):
self.val = val
self.left= left
self.right=right
class solution:
def T2S(root):
def helper(root,string):
if not root:
string += "None,"
return string
else:
string += str(root.val)+ ","
string = helper(root.left,string)
string = helper(root.right,string)
return string
return helper(root,"")
def S2T(data):
datalist = data.split(",")
def helper(data):
if data[0] == "None":
data.pop(0)
return None
nums = data.pop(0)
root = node(nums)
root.left = helper(data)
root.right= helper(data)
return root
return helper(datalist)
def show(root):
print(root.val)
if root.left:solution.show(root.left)
if root.right:solution.show(root.right)
root = node(1)
root.left = node(2)
root.right= node(3)
root.right.left = node(4)
root.right.right= node(5)
print(solution.T2S(root))
Sdata = solution.T2S(root)
S2T = solution.S2T(Sdata)
solution.show(S2T)
勉強させてもらいました。
分からないことが分かると楽しいですね(笑)


