こんばんは(*´ω`)
いつも応援有難う御座います。
今回は迷路です。
Start から Goal まで"何手"必要なのか見ていきます。
以下にあるサンプルの迷路は、
有難く有識者の遺産を拝借いたしました m(_ _)m
# "#" は壁
# "S" は Start 地点、"G" は Goal 地点
# "." は道
maze = [
['#', 'S', '#', '#', '#', '#', '#', '#', '.', '#'],
['.', '.', '.', '.', '.', '.', '#', '.', '.', '#'],
['.', '#', '.', '#', '#', '.', '#', '#', '.', '#'],
['.', '#', '.', '.', '.', '.', '.', '.', '.', '.'],
['#', '#', '.', '#', '#', '.', '#', '#', '#', '#'],
['.', '.', '.', '.', '#', '.', '.', '.', '.', '#'],
['.', '#', '#', '#', '#', '#', '#', '#', '.', '#'],
['.', '.', '.', '.', '#', '.', '.', '.', '.', '.'],
['.', '#', '#', '#', '#', '.', '#', '#', '#', '.'],
['.', '.', '.', '.', '#', '.', '.', '.', 'G', '#'],
]
上記は要素間にカンマがあったり、
スペースがあって分かりにくいですね。
もう少し、表示を分かり易くしてみましょう。
具体的には以下の記述で表示し直してみました。
def print_maze(maze):
for xx in maze:
for yy in xx:
print(yy,end="")
print()
print_maze(maze)
# 実行結果
# S######.#
......#..#
.#.##.##.#
.#........
## .##.####
....#....#
.#######.#
....#.....
.####.###.
....#...G#
あとは、迷路に迷ってみるとは言いつつも、
Start と Goal の座標は予め分かっているものとします。
sx, sy = 0, 1 # スタート地点の座標
gx, gy = 9, 8 # ゴール地点の座標
前述の迷路だけではイメージが難しいので、
やはり迷路を綺麗に書き直すことにします。

黒が壁になりますので、水色の道を辿って、"S" から "G" まで向かいます。
基本的には"道"となる座標を選んでいくのですが、注意点があります。
1.壁を突き破って歩けない
2.一度通った道は、二度と通れない
1 は、迷路の構成を把握していれば問題なさそうですが、
2 に関しては自分で何処を通っていたかメモしていないと無理そうです。
なので以下の図にあるように、迷路の地図だけでなく、メモを持っておく必要があります。

スタートからゴールまで何手で着いたかを調べるので、
自分が歩いた座標に、カウント数をメモして進んでいきましょう。
よって、ゴールにたどり着いたときのメモの数字を返せばミッション終了です。
勝手なイメージですけど、こんな感じなのでしょうか。

どのように進むかは置いておいて、
メモを作るとこまで記載したいと思います。
def print_maze(maze):
for xx in maze:
for yy in xx:
print(yy,end="")
print()
def make_memo():
none = None
field_x_length = len(maze[0]) # x 方向の要素数
field_y_length = len(maze) # y 方向の要素数
# [ None for i in range(4)] とかやってみると以下の記述の意味が分かります
distance = [[none for i in range(field_x_length)] for j in range(field_y_length)]
print_maze(distance)
maze = [
['#', 'S', '#', '#', '#', '#', '#', '#', '.', '#'],# <== maze[0]
['.', '.', '.', '.', '.', '.', '#', '.', '.', '#'],# <== maze[1]
['.', '#', '.', '#', '#', '.', '#', '#', '.', '#'],# <== maze[2]
['.', '#', '.', '.', '.', '.', '.', '.', '.', '.'],# <== maze[3]
['#', '#', '.', '#', '#', '.', '#', '#', '#', '#'],# <== maze[4]
['.', '.', '.', '.', '#', '.', '.', '.', '.', '#'],# <== maze[5]
['.', '#', '#', '#', '#', '#', '#', '#', '.', '#'],# <== maze[6]
['.', '.', '.', '.', '#', '.', '.', '.', '.', '.'],# <== maze[7]
['.', '#', '#', '#', '#', '.', '#', '#', '#', '.'],# <== maze[8]
['.', '.', '.', '.', '#', '.', '.', '.', 'G', '#'],# <== maze[9]
]
print_maze(maze)
make_memo()
# 迷路 : print_maze(maze)
# S######.#
......#..#
.#.##.##.#
.#........
## .##.####
....#....#
.#######.#
....#.....
.####.###.
....#...G#
# メモ : make_memo()
NoneNoneNoneNoneNoneNoneNoneNoneNoneNone
NoneNoneNoneNoneNoneNoneNoneNoneNoneNone
NoneNoneNoneNoneNoneNoneNoneNoneNoneNone
NoneNoneNoneNoneNoneNoneNoneNoneNoneNone
NoneNoneNoneNoneNoneNoneNoneNoneNoneNone
NoneNoneNoneNoneNoneNoneNoneNoneNoneNone
NoneNoneNoneNoneNoneNoneNoneNoneNoneNone
NoneNoneNoneNoneNoneNoneNoneNoneNoneNone
NoneNoneNoneNoneNoneNoneNoneNoneNoneNone
NoneNoneNoneNoneNoneNoneNoneNoneNoneNone
ではでは、用意したフィールドを進んでいきましょう。
!?
そう、フィールドです。
フィールドって言われたら、勿論、座標がありますよね?
(あれ?ちょっと強引!?( ゚Д゚))
ちょっと座標を振ってみました。

何処をどのように進むかをメモするにも座標がないと何もできませんから
まぁ、定義するのは自然な流れかもしれません。
あとは、進む方向です。
例えばですが、→(右) であれば前述の座標を考えると(x:1, y:0)ですよね?
ザクっと四方向の進み方を以下にまとめました。
→ 右 (x: 1,y: 0)
← 左 (x:-1,y: 0)
↑ 上 (x: 0,y:-1)
↓ 下 (x: 0,y: 1)
ある地点から、for 文で上記を全て回した時の座標が以下の条件を満たしていれば良いと思いませんか?
- 壁ではない
- 定義した座標から飛び出ない
- 今まで行ったことのない場所
さっそく書いてみましょう!!
for i in range(4):#上下左右を指定するために 4 とする
#nx,ny :移動先の座標 , x,y : 現在の座標
nx, ny = x + [1, 0, -1, 0][i], y + [0, 1, 0, -1][i] # nx,ny = x + X[i], y + Y[i] と等価です
# i = 0 : nx , ny = x + 1, y + 0 .... → 右 (x: 1,y: 0)
# i = 1 : nx , ny = x + 0, y + 1 .... ↑ 上 (x: 0,y:-1)
# i = 2 : nx , ny = x +-1, y + 0 .... ← 左 (x:-1,y: 0)
# i = 3 : nx , ny = x + 0, y +-1 .... ↓ 下 (x: 0,y: 1)
# |←-----横軸 x を飛び出ない-----→| |←-----縦軸 y を飛び出ない-----→|
if (0 <= nx and nx < field_x_length and 0 <= ny and ny < field_y_length \
#|←-壁は突き破らない!-→| |←-----初めての場所!------→|
and maze[nx][ny] != '#' and distance[nx][ny] == none):
#distance[x][y]:現在地 + 1 の値をdistance[nx][ny]にメモ
distance[nx][ny] = distance[x][y] + 1
あとはスタートから始まって、ゴールに着くまで
前述の処理を繰り返せばゴールに何手で着いたか分かると思います。
はて(・・?
どうやって制御しましょう。。。
困ったときは、前述にあるように
ザクっと書いたやりたいこと(プログラム)を動かして
動作を図にしてみます。きっと足りない点が見えてくるはず。
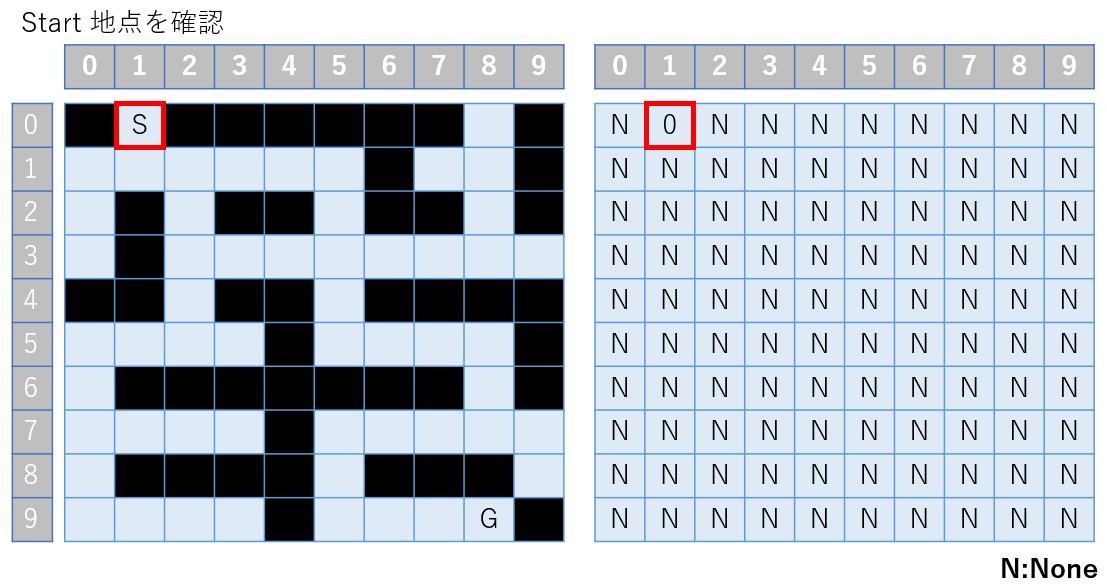
ここは問題ありませんね。
ではここから上下左右に動いてみます。
その時、前述の制約を考えると進めるのは。。。

では次のマスで上下左右を試してみましょう。
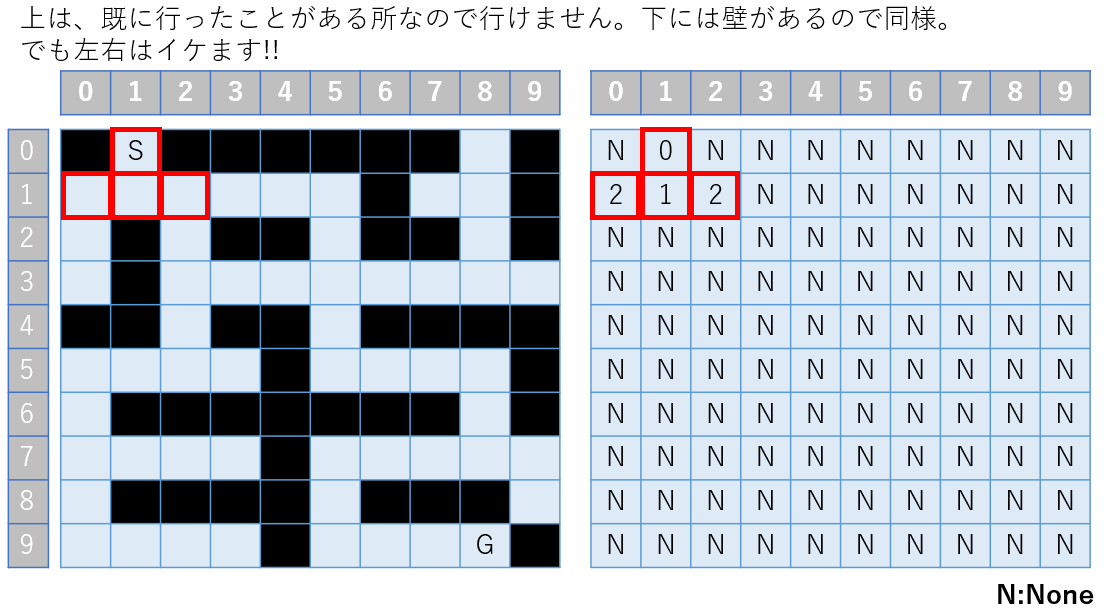
あらら!? 二手に分かれちゃいました。
[0,1] , [2,1] の座標でそれぞれ四方に動く処理をする必要が出てきました。
バッファして、それぞれの場合を処理することで分岐を処理することが出来ませんか?
今回はキューを使います。これには理由があります。
前回の [部分和と向き合ってみる] (https://qiita.com/AKpirion/items/390006b735b1b4d7ea0c)では分岐点が出来たら、
どちらかの道を選択し、行き止まりになるまで進み切っていました(深さ優先探索)。
でもキューとして分岐点の座標を Fast in Fast out することで、
分岐点の両方の座標を処理してから次の下層の処理ができますよね?
以下にあるように 赤 => 青 => 緑とそれぞれの層を処理してから下層に向かって処理しているイメージになります。

これを幅優先探索と言うらしいです。
逆にキューをスタックに変えれば深さ優先探索になります。
分かりにくかったり、間違っていたらコメント御願い致します m(_ _)m
さて、運よく、ゴールの手前まで来たとします。
その時はこんな感じでしょうか。
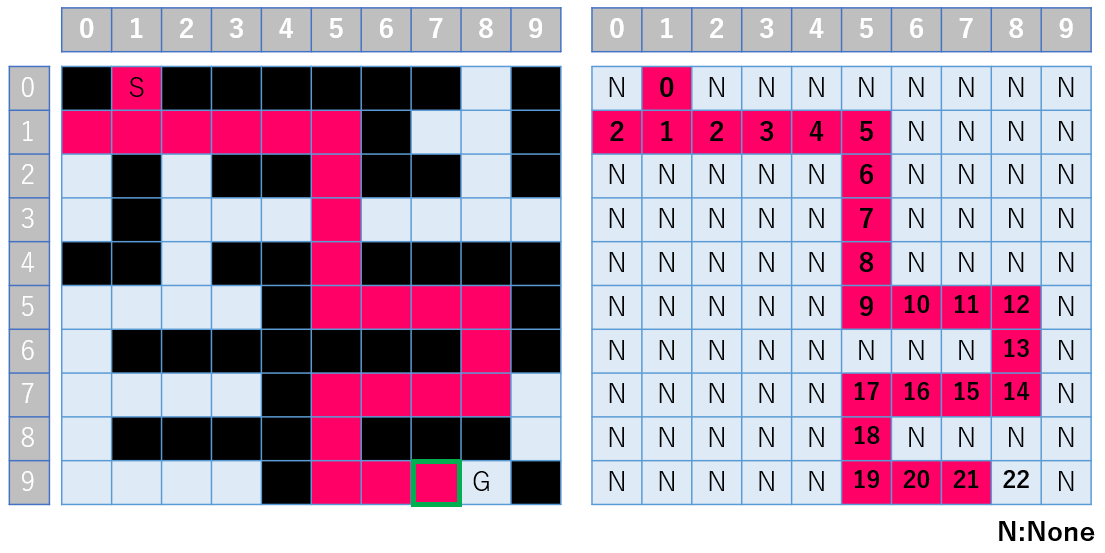
※面倒なので最短経路だけ赤く塗っています。本当は分岐に分岐を繰り返すので、道路(水色)のマスは、一通り赤くなるはずですm(_ _)m
左上の図にある緑の枠を見てください。
ゴール直前に着た以上は、右に行くしかないのは当然なのですが、ポイントは
ゴール直前であってもキューにバッファしているデータ長は 0 になることはない事を意味しています。
以上から進行方向を決めて進む処理を while 文で繰り返し行い、
特定の座標に着いたら break すれば良いのです。
def solve_maze(sx, sy, gx, gy, maze):
none = None
field_x_length = len(maze[0])
field_y_length = len(maze)
distance = [[none for i in range(field_x_length)] for j in range(field_y_length)]
buff = []#座標をバッファ
buff.append([sx, sy])#start 座標を追加
distance[sx][sy]=0#start 座標にある None を 0 に書き換える
while len(buff):# len(buff) == 0 になるまでループ
x,y = buff.pop(0)#現在地の更新
if x == gx and y == gy:#goal に着いたら break
break
for i in range(4):
nx, ny = x + [1, 0, -1, 0][i], y + [0, 1, 0, -1][i]
if (0 <= nx and nx < field_x_length and 0 <= ny and ny < field_y_length \
and maze[nx][ny] != '#' and distance[nx][ny] == none):
buff.append([nx,ny])#進めそうな座標をバッファ
distance[nx][ny] = distance[x][y] + 1
#メモの最終結果を表示
print_maze(distance)
#最後にゴール地点のメモを返す
return distance[gx][gy]
# メモの結果
None0NoneNoneNoneNoneNoneNone13None
212345None1312None
3None3NoneNone6NoneNone11None
4None4567891011
NoneNone5NoneNone8NoneNoneNoneNone
8767None9101112None
9NoneNoneNoneNoneNoneNoneNone13None
10111213None1716151415
11NoneNoneNoneNone18NoneNoneNone16
12131415None19202122None
# ゴールまでの距離
22
すいません、分かりにくいので図にします。
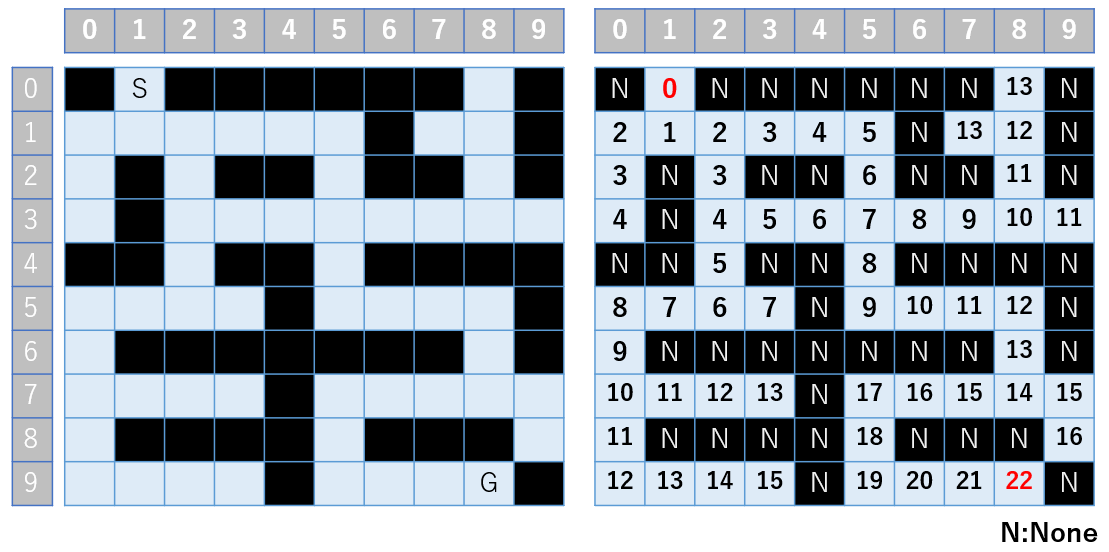
プログラムってこんなことが出来るんですね( ..)φメモメモ
勉強になりました('◇')ゞ