TL;DR
情報系の授業でよくあるようなデータ構造をSwiftで実装しました.
実装したのは二つ.
- 単方向線形リスト
- 二分探索技
単方向線形リスト
単方向線形リストとは
線形リストとは一次元配列のようなデータ列のことを言います.
データと次のノードへのポインタを持つ構造体を連結したものです.
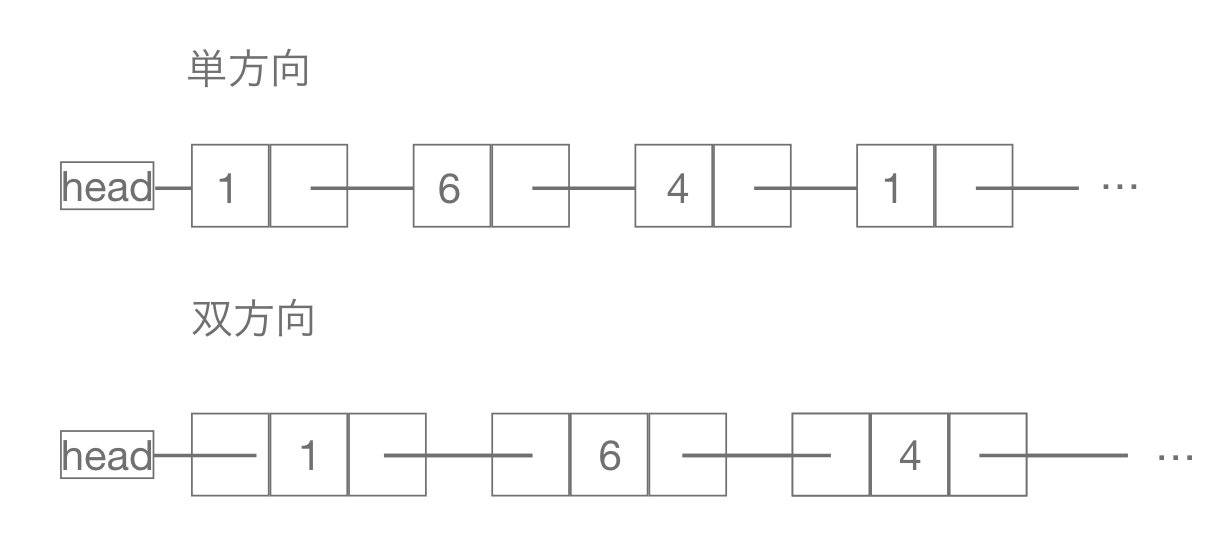
単方向は次のノードへのポインタのみを持ち, 双方向は前と次のノードへのポインタを持ちます.
配列との違い
配列はデータがメモリ上に連続して格納されますが、線形リストは連続して格納されるとは限りません.
線形リストは値を持つノードが次の値を持つノードへのポインタを持つことでデータ列として表現されています.
図2. メモリへの格納の違い

実装
構造体自体と諸々のメソッドを実装します.
まず, 上で説明した構造体を作ります.
LinkedListは先頭要素へのポインタを持ちます. これをheadとし, Node型のプロパティにします
また同時にNodeも定義します.
Nodeは, データと次のNodeへのポインタを持ちます.
データをvalue: T, 次のNodeへのポインタ1をNodeとします.
//デバッグしやすいように, TはCustomStringConvertibleを準拠している型とする
class LinkedList<T: CustomStringConvertible> {
var head: Node<T>? = nil
class Node<T> {
var value: T
var next: Node<T>?
init(value: T) {
self.value = value
}
}
}
リストの末尾へ追加(append)
末尾への追加は単純で, next == nil のNodeに対し, 新しいNodeをつないであげるだけです.
最後尾へのリンクを持っていないのでオーダーは$\Theta (n)$になります.
public func append(_ element: T) {
guard var ptr = head else {
head = Node<T>(value: element)
return
}
while let next = ptr.next {
ptr = next
}
ptr.next = Node<T>(value: element)
}
指定のindexへ挿入(insert)
insertは第二引数の値を持ったNodeを生成して, 第一引数のindexへ追加します.
indexが不正な値の場合, 例外を発生させます.
append同様, 指定のindexまで走査するのでオーダーは, $\Theta (n)$になります.
public func insert(index: Int, element: T) throws {
let node = Node<T>(value: element)
if index < 0 || index > count() {
throw NSError(domain: "out of range", code: -1, userInfo: nil)
}
if index == 0 {
node.next = head
head = node
} else {
var ptr = head
for _ in 0..<index-1 {
ptr = ptr?.next
}
node.next = ptr?.next
ptr?.next = node
}
}
指定のindexを取得(get)
引数で与えたindex番目のNodeを取得します.
オーダーは, index番目まで走査を行うので, $\Theta (n)$です.
public func get(at index: Int) -> Node<T>? {
var cnt = 0
var ptr = head
while let next = ptr?.next, cnt < index {
cnt += 1
ptr = next
}
return ptr
}
指定のindexを削除(remove)
引数で与えたindex番目のnodeを削除します.
指定indexの一つ前のnodeのnextを張り替えることで実現しています.
public func remvove(at index: Int) throws {
if index < 0 || index > count() {
throw NSError(domain: "out of range", code: -1, userInfo: nil)
}
if index == 0 {
head = head?.next
} else {
var ptr = head
for _ in 0..<index-1 {
ptr = ptr?.next
}
ptr?.next = ptr?.next?.next
}
}
二分探索木
二分探索木とは
二分探索木は「左の子の値 ≤ 親の値 ≤ 右の子の値」という制約がついた二分木のことを言います.
計算量は探索, 挿入, 削除のいずれも$\Theta(logN)$となります.
実装
データ構造
値と左部分木, 右部分木, 親を持つようにします.
親がnilの場合, rootとなります.
また, 値は順序がついている必要があるため, TはComparableを準拠しています.
class BinarySearchTree<T: Comparable & CustomStringConvertible> {
var value: T
var left: BinarySearchTree? = nil
var right: BinarySearchTree? = nil
var parent: BinarySearchTree? = nil
init(_ v: T) {
value = v
}
}
データの列挙
preorder, inorder, postorderの三つを実装しました.
特に言うことはないかなと思います.
func preOrderPrint() {
print(value.description)
if let left = left {
left.preOrderPrint()
}
if let right = right {
right.preOrderPrint()
}
}
func inOrderPrint() {
if let left = left {
left.inOrderPrint()
}
print(value.description)
if let right = right {
right.inOrderPrint()
}
}
func postOrderPrint() {
if let left = left {
left.postOrderPrint()
}
if let right = right {
right.postOrderPrint()
}
print(value.description)
}
探索
引数で与えた値が存在するかどうかを判別します.
ノードの値が一致していたらtrueを返します.
引数値がノードの値より小さいならば左部分木で再帰し、
引数値がノードの値より大きいならば右部分木で再帰します.
func search(v: T) -> Bool {
if v == value {
return true
} else if v < value {
if let left = left {
return left.search(v: v)
} else {
return false
}
} else {
if let right = right {
return right.search(v: v)
} else {
return false
}
}
}
挿入
再帰の仕方は探索と同じです.
もしノードが葉であれば, 値を挿入します.
func add(_ v: T) {
if v < self.value {
if let left = left {
left.add(v)
} else {
left = BinarySearchTree(v)
left?.parent = self
}
} else {
if let right = right {
right.add(v)
} else {
right = BinarySearchTree(v)
right?.parent = self
}
}
}
削除
func max() -> BinarySearchTree {
if let right = right {
return right.max()
} else {
return self
}
}
func remove(v: T) {
if v == value {
if let left = left, let right = right { // branch
let leftMax = left.max()
self.value = leftMax.value
leftMax.remove(v: leftMax.value)
} else if let left = left, right == nil { // only left
self.value = left.value
self.left = left.left
self.right = left.right
} else if let right = right, left == nil { // only right
self.value = right.value
self.right = right.right
self.left = right.left
} else { // leaf
self.parent = nil // 接続を切る
}
} else if v < value {
left?.remove(v: v)
} else {
right?.remove(v: v)
}
}
まとめ
プログラミングの基礎中の基礎のような記事になりましたが, 意外と役に立つ時が来るかもしれませんね.
今回の全体のコードはgistにあげておきます.
gist
記事を書いている途中に面白いリポジトリを見つけたので載せておきます.(少し参考にさせていただきました)
swift algorithm club
-
Swiftにおいてclassのプロパティは参照が代入されるのでポインタと見て問題ないかと思います. ↩