久々の投稿。
Moneroの匿名性
Moneroが匿名通貨と呼ばれる所以は以下の3つがある。
- 送金元が誰か分からない = どのUTXOを入力したか分からない
- 送金額がいくらか分からない = 送金額の暗号化
- 受取アドレスを使い捨てる = 送金先が誰か分からない
このうち1.と2. にリング署名が使われている。ちなみに3. の使い捨てるアドレスはステルスアドレス(stealth address)と呼ばれる。
Moneroのリング署名の特徴
- 楕円曲線にはed25519を使用。
- ハッシュ関数は**SHA3(keccak)**を使用。
ed25519楕円曲線
q=2^{255}-19 \\
-x^{2}+y^{2}=1-\frac{121665}{121666}x^{2}y^{2} \\
L = 2^{252} + 27742317777372353535851937790883648493 \\
今回使用したPython実装は、ed25519.pyを高速化したこちらのライブラリ。数学的な説明はed25519のpython実装を紐解く その1数学編で詳しくなされている。暗号を作る仕組みはビットコインの楕円曲線暗号と変わらないと考えて良い。
ちなみにEd25519のベースポイントGは、
x=15112221349535400772501151409588531511454012693041857206046113283949847762202\\
y=46316835694926478169428394003475163141307993866256225615783033603165251855960
と定義されており、ed25519.py内ではBx、Byに代入されている。
このベースポイントを点のスカラーk倍(ここで、kは上記Lを最大とする整数 $k\in Z_{L}$)したed25519上の点$kG$を与えられた時、$k$を逆算することはおよそ不可能であることから、秘密鍵を$k$とした時、公開鍵を$K=kG$と表すことができる。
def gen_keypair(n=0):
sk = rand(n) # 秘密鍵 (secret key)
PK = scalarmult_base(sk) # 公開鍵 (Public key)
return sk, PK
Schnorr署名
リング署名に後々応用される署名方式としてSchnorr署名をまず説明する。
メッセージMを秘密鍵kで署名する場合、手順は以下の通りである。
署名の手順
- ランダムな整数 $\alpha \in Z_{L}$ を選び、$Q=\alpha G$を得る。
- $e = H(M||Q)$を計算。ここで$||$は文字列の足し算とする。また、$H$はkeccakハッシュ関数。
- $s = \alpha - ek$ を計算する。ここで$s \in Z_{L}$となる。
- 署名として $\sigma = (s,e) $ を得る。
認証者は上記の$\sigma$と公開鍵$K$を使って認証する。
認証の手順
- $Q=sG+eK$を計算。
- $e = H(M||Q)$で手に入る$e$が、署名に含まれている$e$と等しければ認証成功。
途中式は以下のようになっている。
Q=sG+eK=(\alpha -ek)G+eK\\=\alpha G-ekG+eK\\=\alpha G-eK+eK\\=\alpha G\\=Q
# 署名
def schnorr_signature(M,sk_hex):
alpha_hex = rand()
Q_hex = scalarmult_base(alpha_hex)
e_hex = H(M.encode()+Q_hex)
alpha_int = ed25519.decodeint(binascii.unhexlify(alpha_hex))
e_int = ed25519.decodeint(binascii.unhexlify(e_hex))
sk_int = ed25519.decodeint(binascii.unhexlify(sk_hex))
s_int = (alpha_int - e_int*sk_int) % ed25519.l
s_hex = binascii.hexlify(ed25519.encodeint(s_int))
return e_hex,s_hex
# 認証
def schnorr_verify(M,PK_hex,e_hex,s_hex):
sG_hex = scalarmult_base(s_hex)
eP_hex = scalarmult(PK_hex, e_hex)
sG = ed25519.pt_xform( ed25519.decodepoint(binascii.unhexlify(sG_hex)) )
eP = ed25519.pt_xform( ed25519.decodepoint(binascii.unhexlify(eP_hex)) )
Q_pt = ed25519.pt_unxform( ed25519.xpt_add(sG,eP) )
Q_hex = binascii.hexlify(ed25519.encodepoint(Q_pt))
ee_hex = H(M.encode()+Q_hex)
return e_hex == ee_hex
hex、int、ed25519の点と、変数の型のencode&decodeは関数の外でやれよ。。と思った方今回は見逃してください。。。
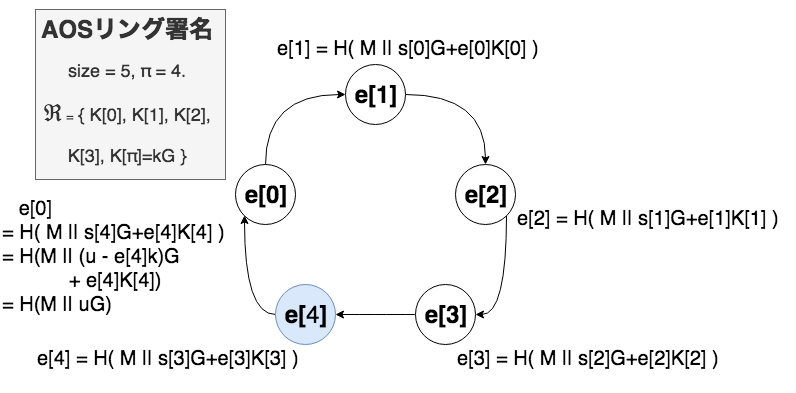
AOSリング署名
では、本記事の本題であるリング署名について説明する。
リング署名は上記ed25519楕円曲線上の点である公開鍵$K_i$を複数個集めて偽物、囮として使う。それらをリングメンバー$\Re$と呼び、そのリングメンバーに自分の公開鍵$K_\pi = k_\pi G$を混ぜ、メッセージを自分の秘密鍵$k_\pi$を使って署名をする。署名を見ただけでは第三者は$\Re= \langle K_0,K_1,...,K_i,...,K_{n-1} \rangle$の公開鍵のうちどれが$K_\pi$なのかを知ることができない。にも関わらず、メッセージが$\Re$のうちどれかの秘密鍵$k_\pi$で署名されたことを証明できる。
まず例を見てみよう。
リングの大きさ=3の場合
署名したいメッセージを$M$とし、リングメンバーを$\Re=\langle K_0,K_1,K_2 \rangle$とする。また、今回は署名者のインデックス$\pi=1$とする。つまり、署名者自身からは$\Re=\langle K_0,K_\pi,K_2 \rangle$、$K_\pi=k_\pi G$という風に見える。
署名手順(リングの大きさ=3、$\pi=1$の場合)
0. 手元には$\Re= \langle K_1,K_\pi,K_2 \rangle$、秘密鍵$k_\pi$、メッセージ$M$がある。
1. $u \in Z_L$をランダムに選ぶ。
2. $e_2 = H(M||uG)$を計算。(この2は$2=\pi+1=1+1$から来ている。)
3. $s_2 \in Z_L$をランダムに選ぶ。
4. $e_0 = H(M||s_2G+e_2K_2)$を計算。(この0は、サイズ3のリングにおける2の次のインデックスを指す。)
5. $s_0 \in Z_L$をランダムに選ぶ。
6. $e_1 = H(M||s_0G+e_0K_0)$を計算。(この1は、サイズ3のリングにおける0の次のインデックスを指す。)
7. $s_1 = u-e_1k_1$を計算。($u$はステップ1.で選んだもの。また、$k_1=k_\pi$であることを思い出してほしい。)
8. $\sigma=(e_0,s_0,s_1,s_2)$が署名となる。end.
ちなみに$\pi=2$の場合、ステップ2.は$e_0$から計算を始めて$s_2$の計算で終わり、$\pi=0$の場合$e_1$から始めて$s_0$で終わる。よって、最後に得られる$\sigma$を見るだけでは実際に署名に使われた鍵がどの場所にあるのかは分からない。
これだけでは何を言っているか分からないと思うので認証の手順を見てみよう。認証には$\pi$を知る必要がない。というより知っていたら匿名署名と言えない。
認証手順(リングの大きさ=3の場合。)
0. 手元には$\Re= \langle K_0,K_1,K_2 \rangle$、メッセージ$M$、署名$\sigma=(e_0,s_0,s_1,s_2)$がある。
1. $e_1=H(M||s_0G+e_0K_0)$を計算。
2. $e_2=H(M||s_1G+e_1K_1)$を計算。
3. $e_0'=H(M||s_2G+e_2K_2)$を計算。
4. $e_0'$が$e_0$に一致したら認証成功。end.
インデックス1から$e_i$を計算していき、最初の$e_0$にぐるりと戻って来ることができればいい。リング署名がリングと呼ばれる所以がここにある。
リングの大きさ=Nの場合
上記の例が理解できればリングのサイズが$N$であろうと、$\pi$が何であろうと、署名と認証がどう行われるかは容易に想像がつくはずだ。
署名は$e_{\pi+1}$から始めて、$e_{\pi+2}$, $e_{\pi+3}...e_{N-1},e_0$...と一周回って$e_{\pi}$まで計算を続ける*(インデックスはmod Nと表せる)*。最後、$s_\pi=u-e_\pi k_\pi$を求めれば、署名$\sigma=(e_0,s_0,s_1,...,s_{N-1})$が得られる。
認証も簡単で、$e_1$から$e_2$...と計算していき、ぐるりと$e_0$に戻って来られればいい。
ちなみに本記事の最初に紹介したSchnorr署名はAOSリング署名の$N=1$版と考えることができる。
よく見る図に数式を添える
リング署名について解説しているサイトでは大抵、何かリングのような図を使うものの、数式がないために結局何が言いたいのか分からないことが多い。あくまで筆者の基準だが、少しでも説明が分かりやすくなるような図を作った。
図と数式を見比べると、真の秘密鍵$k_\pi$はリングを閉じる役割を持っていることが分かる。
AOSリング署名の実装
def aos_ring_signature(M,decoy_group,PK_hex,sk_hex,index_pi=-1):
M_encoded = M.encode()
index_pi = random.randint(0,len(decoy_group)) if index_pi == -1 else index_pi
PK_pi = PK_hex
decoy_group.insert(index_pi,PK_pi)
e = [0]*len(decoy_group)
s = [0]*len(decoy_group)
u_hex = rand(0)
uG_hex = scalarmult_base(u_hex)
index_start = (index_pi+1) % len(decoy_group)
e[index_start] = H(M_encoded+uG_hex)
s[index_start] = rand(0)
for cnt in range(1,len(decoy_group)):
i = (index_start+cnt) % len(decoy_group)
prev_i = (i-1) % len(decoy_group)
s[i] = rand(0) if i != index_pi else 0
temp = pt_add_hex(scalarmult_base(s[prev_i]),scalarmult(decoy_group[prev_i], e[prev_i]))
e[i] = H(M_encoded+temp)
u_int = ed25519.decodeint(binascii.unhexlify(u_hex))
e_int = ed25519.decodeint(binascii.unhexlify(e[index_pi]))
sk_int = ed25519.decodeint(binascii.unhexlify(sk_hex))
s[index_pi] = binascii.hexlify(ed25519.encodeint((u_int-e_int*sk_int) % ed25519.l))
return e[0],s,decoy_group
def aos_ring_verify(M,PK_list,e0,s_list):
M_encoded = M.encode()
e = [0]*len(s_list)
e[0] = e0
for i in range(1,len(PK_list)):
temp = pt_add_hex(scalarmult_base(s_list[i-1]),scalarmult(PK_list[i-1], e[i-1]))
e[i] = H(M_encoded+temp)
temp = pt_add_hex(scalarmult_base(s_list[-1]),scalarmult(PK_list[-1], e[-1]))
e[0] = H(M_encoded+temp)
return e0==e[0]
Borromeanリング署名
メッセージを複数のリングで署名する場合はBorromeanリング署名という方式を使う。Moneroでもリングが2つ使われるためBorromeanリング署名が使われている部分がある。
リングが複数というのはつまり、$\Re_0, \Re_1, ..., \Re_{m-1}$と$m$個のリングメンバーがあるということである。そして、それぞれの$\Re_i=\langle K_{i,0},K_{i,1},...,K_{i,j},...,K_{i,N_i-1} \rangle$のうち、$K_{i,\pi}=k_{\pi_i}G$をどれか分からなくしてメッセージを署名することができる。
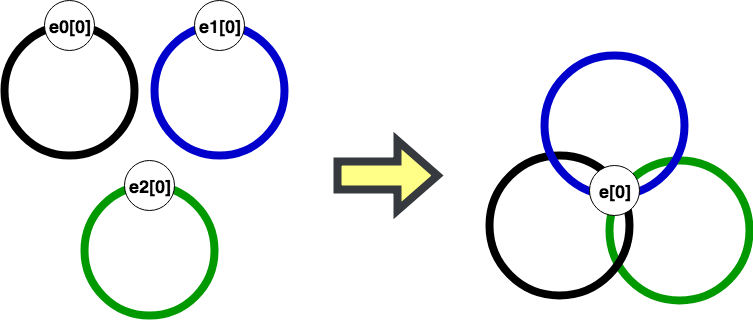
上の図のように、もしリングが複数($m$個)ある場合、繋ぐポイントをひとまとめにすることで署名のデータ量を減らすことができる。つまり、
\sigma_0=(e_{0,0},s_{0,0},s_{0,1},...,s_{0,N_0-1}), \\ \sigma_1=(e_{1,0},s_{1,0},s_{1,1},...,s_{1,N_1-1}), \\... \\ \sigma_m=(e_{m,0},s_{m,0},s_{m,1},...,s_{m,N_m-1})
を合わせて署名$\Sigma=(\sigma_0,\sigma_1,...,\sigma_M)$とする代わりに、
\Sigma=(e_0,s_{0,0},...,s_{0,N_0-1}, s_{1,0},...,s_{1,N_1-1}, ..., s_{m,0},...,s_{m,N_m-1})
とすることで署名$\Sigma$に含まれる値の数を$m-1$個減らすことができる。
署名手順
1. $\forall{i}$, $\Re_i$において、$e_{\pi_i+1}=H(M ||u_iG)$を計算。$u_i\in Z_L$は乱数。
2. $\forall{i}$, $\Re_i$において続きのインデックス$j$、$\pi_i<j<N_i$まで、$e_{i,j}=s_{i,j-1}G+e_{i,j-1}K_{i,j-1}$を計算。$s_{j-1}\in Z_L$は乱数。【例外】もし、ステップ1. ですでに最後のインデックスまで辿り着いた(=真の秘密鍵のインデックスがそのリングの最後。つまり$\pi_i=N_i-1$)場合はこのステップは飛ばす。
3. $\forall{i}$, $\Re_i$における$R_i=s_{i,N_i-1}G+e_{i,N_i-1}$を計算。ステップ2. を飛ばしたリングにおいては$R_i=u_iG$とする。
4. $e_0=H(M||R_0||R_1||...||R_{m-1}) $を計算。
5. $\forall{i}$, $\Re_i$において、インデックス$j$の$1\leq j\leq \pi_i$まで、$e_{i,j}=s_{i,j-1}G+e_{i,j-1}K_{i,j-1}$を計算。$s_{j-1}\in Z_L$は乱数。
6. $\forall{i}$, において$s_{i,\pi_i}=u_{i}-e_{i,\pi_i}k_{\pi_i}$を求める。end.
認証は、ステップ4. の$e_0$からAOSリング署名の認証方法でそれぞれのリング$\Re_i$をぐるりと一周して得られる$e_{0}'$が$e_0$と一致すれば認証成功となる。
Borromeanリング署名の実装
# Borromean Ring Signatures
def borromean_ring_signature(M, PK_matrix, PK_vector, sk_vector,index_pi=-1):
M_encoded = M.encode()
index_pi = [0]*len(PK_matrix)
u_hex = [0]*len(PK_matrix)
uG_hex = [0]*len(PK_matrix)
R = [0]*len(PK_matrix)
e = [None]*len(PK_matrix)
s = [None]*len(PK_matrix)
for row in range(0,len(PK_matrix)):
# set index_pi
index_pi[row] = random.randint(0,len(PK_matrix[row])) if index_pi==-1 else index_pi[row]
# insert pk
PK_matrix[row].insert(index_pi[row],PK_vector[row])
e_row = [0]*(len(PK_matrix[row]))
s_row = [0]*(len(PK_matrix[row]))
# for connecting point
u_hex[row] = rand(0)
uG_hex[row] = scalarmult_base(u_hex[row])
index_start = (index_pi[row] + 1) % len(PK_matrix[row])
### case B1: [0,...,0,pi,st]
if index_start == len(PK_matrix[row])-1:
e_row[index_start] = H(M_encoded+uG_hex[row])
s_row[index_start] = rand(0)
R[row] = pt_add_hex(scalarmult_base(s_row[index_start]),scalarmult(PK_matrix[row][index_start], e_row[index_start]))
### case B2: [0,...,pi,st,...,0]
elif index_start > 0:
e_row[index_start] = H(M_encoded+uG_hex[row])
s_row[index_start] = rand(0)
for i in range(index_start+1,len(PK_matrix[row])):
temp = pt_add_hex(scalarmult_base(s_row[i-1]),scalarmult(PK_matrix[row][i-1], e_row[i-1]))
e_row[i] = H(M_encoded+temp)
s_row[i] = rand(0)
if i == len(PK_matrix[row])-1:
R[row] = pt_add_hex(scalarmult_base(s_row[i]),scalarmult(PK_matrix[row][i], e_row[i]))
### case B3: [st,0,0,...,0,pi]
else:
R[row] = uG_hex[row]
e[row] = e_row
s[row] = s_row
R_sum = b''
for i in range(0,len(R)):
R_sum += R[i]
# set common e0
e0 = H(M_encoded+R_sum)
for row in range(0,len(PK_matrix)):
e[row][0] = e0
s[row][0] = rand(0)
### case C1: [pi,st,0,...]
if index_pi[row] == 0:
u_int = ed25519.decodeint(binascii.unhexlify(u_hex[row]))
e_int = ed25519.decodeint(binascii.unhexlify(e0))
sk_int = ed25519.decodeint(binascii.unhexlify(sk_vector[row]))
s[row][0] = binascii.hexlify(ed25519.encodeint((u_int-e_int*sk_int) % ed25519.l))
### case C2: [0,pi,st,0,...] or [st,0,0,...,0,pi]
else:
# i up to pi (inclusive)
for i in range(1,index_pi[row]+1):
prev_i = i-1
s[row][i] = rand(0)
temp = pt_add_hex(scalarmult_base(s[row][prev_i]),scalarmult(PK_matrix[row][prev_i], e[row][prev_i]))
e[row][i] = H(M_encoded+temp)
u_int = ed25519.decodeint(binascii.unhexlify(u_hex[row]))
e_int = ed25519.decodeint(binascii.unhexlify(e[row][index_pi[row]]))
sk_int = ed25519.decodeint(binascii.unhexlify(sk_vector[row]))
s[row][index_pi[row]] = binascii.hexlify(ed25519.encodeint((u_int-e_int*sk_int) % ed25519.l))
return e0,s,PK_matrix
def borromean_verify(M,PK_matrix,e0,s_matrix):
M_encoded = M.encode()
R = [0]*len(PK_matrix)
for row in range(len(PK_matrix)):
e = [0]*len(s_matrix[row])
e[0] = e0
for i in range(1,len(PK_matrix[row])):
temp = pt_add_hex(scalarmult_base(s_matrix[row][i-1]),scalarmult(PK_matrix[row][i-1], e[i-1]))
e[i] = H(M_encoded+temp)
if i == len(PK_matrix[row])-1:
R[row] = pt_add_hex(scalarmult_base(s_matrix[row][i]),scalarmult(PK_matrix[row][i], e[i]))
R_sum = b''
for each in R:
R_sum += each
return e0 == H(M_encoded+R_sum)
Moneroではどう使われているか
例えばこのトランザクションを見てみよう。
ring memberにある11個の公開鍵(ステルスアドレス)のうち1つが真のインプット(入力アドレス)である。他の10個は目くらまし用だ。
4fce62db0e3339b5f18642eeb897b5775f8947e874d205a36258c4e6e4d134c5
a0f73a46560e8544c3e48b0de18b763788632e2476992456363394ec4ca657c0
e15d4336814f6c8b21953d6be300598f09194a450ffab287effd5d99aa9847da
6fac2ba283855f4e8d40af6771385cf7ae8171ac70c16e8ce7809484b5817deb
84fa0cc42fb3f8a9b66da2502598d4b9c844635ff1445a96ce22227c034455db
6800a06c38c5c004cffa9e52f1fc1fae4f08853114bca03a67e5eec33d122bdf
d00b482e9009e6fdaf1c10e2470d29a3c132dccd8f2d0d047e12978a3dd44f86
d98c5c74e01b255fc962b783b69a1d72f61cb279f3f69bc45a0142cb60b89210
4d85729d536ff689043c246e995d985579f640d716f2d18f2958c0c0feaa2df2
afb523d7a20d4942580ed3c532b262448b8f48756fdf58c3fc98c3ff0c35f91d
27b3f24ca352c7d01f18c73550eec7f34863cf805f7d67d8cdef204852a0aeb2
それぞれのインプットに対して$m=2$、$N=11$のBorromeanリング署名を行なっている。ちなみにssは$s$、ccは$e_0$に当たる。2つのリングを使っているが、1つ目は入力アドレスを匿名化するためのリング。2つ目はそれぞれの入力金額がpseudoOutsフィールドに暗号化された仮出力金額と等しいことを証明するためのリングである。その仮出力金額の合計がこのトランザクションの暗号化された総出力額に等しいことをマイナーはリング署名を認証することで証明している。
金額の暗号化、ステルスアドレス、key imageなどなど。Moneroには面白いアイデアが盛りだくさんなのだが、長くなりそうなのでそれはまたの別の機会に。。。
"ss": [ [ "73db71a50c83e470c0a1d2a00edf3f949ea529fa77fd7bee51e6ab1655846302", "85ef8f672aa006883d6ee7ab1ecab06be0b0154a9b3afe9fdc7f839c3d135507"],
[ "2c40423e6e6867215a8fd7d43aba6cf8aebed5eb1a3485399e0e9824325b630d", "0d8c91c824e37be7d926b9fee06d52a64b9d69657a14208ae4f4c997aa457702"],
[ "0eea6c3aabf45942f6989ef98f132ce7502f7d8896b7fff92d80aa8dbc265e0e", "8199fb43a819c391f9575869e602e62f4ef7634631403a7d79f8ab39cc65aa09"],
[ "a4d8b67b454a12c933ea491dd30ee48ee0b359f4f26239c28c7c4667389a3b0f", "e128f4a0f998a0ee114dc55a8ce51bce67fc6656a5b9f344258feb9728956101"],
[ "48b34159e8fb3989da22dac8ed6f53f7fcab99ad76db8acbbe06477a80814d0b", "d9009630ed60d287985c4824b70404cb1656bfe967e572d3d82403cddf4c100d"],
[ "68bc788edc72e67320da95a58eead335397115ccbc4f8eca1284d6e014358f00", "5f7c0564c1d12a3b98e4640fcf740badd175774d6f1ff8e893230d5b37cb1f02"],
[ "ece439ef8bb12ec2c10a25b4d48881fd5b1300a4e5a675f5cfbf560a4c209f03", "3053b2ced2afeca36f0392ece047af36feac7fb37889ee9f27235fd5a989190d"],
[ "0d37a831eb7f26ab79c8bde06b504307996d883b13ffa722fc65646ca5d79d0e", "afc42676af7e4f8a487fc1cf73e1447243aee828e85613dfaeb086efeff7d00e"],
[ "ef5170037b21a4f01074a3617334d162381a21990aa45b556749ae0c54459c08", "f407540d896d52dae9a0ecf49dc1ad7fc7a6bfa17471900f93fb6cd981122b0b"],
[ "3d1370d042af97a3a47aac7ac0e14dbdd9d6490d31c4fadefa678b6b660da00e", "90e66a18f346b00c357af0bc9383245a4bbb7159fa9c6b0adcc62857f06cec0f"],
[ "a7abbc0ff0e346e966fb3af8369adeee857ac5283cf2da0333ca82b07ec99a09", "9b5f72e8087b40bfd6b19193bc09aa70a97768ebe574eb734b1078e32152250b"]],
"cc": "e24cb2b656fd38aeb484196552acea60c82f502a40223ee51b5c6a69ec815b07"
参考文献
https://eprint.iacr.org/2015/1098.pdf
https://cryptoservices.github.io/cryptography/2017/07/21/Sigs.html
本記事で実装したコードはGithubにアップした。なお、コードのバグ・脆弱性によって発生した事柄には責任が取れないことをご了承ください。