IOTA【技術解説】署名と承認。 - 改訂版

English here.

#改訂版の背景　
　以前の記事内で更新していない箇所があったため、その結果長い間誤った情報を皆様にお伝えしてしまっていたことをお詫び致します。以前の記事との大きな変更点はハッシュ回数の決定方法です。以前の記事では、ハッシュ回数を単純にトライト9ABCD...Zにおいての9からの距離というふうに説明いたしました。
　しかし、それはバグだったという報告をいただき、最新のソースコードを確認したところ以前とハッシュ回数の決定方法が変わっておりました。
　改訂版ではハッシュ回数についての訂正を行い、旧バージョンで語りきれなかったsecurityという引数による挙動の違いについても言及しました。

CurlとKerl

　IOTAのハッシュ関数。Curlを改正したのがKerl。発音がどう違うのかは不明。IOTAではハッシュ関数を場所ごとに使い分けている。その早見表はこちら。

アドレス生成

　まず、シードからPrivate Keyを生成する。詳細はこちら。
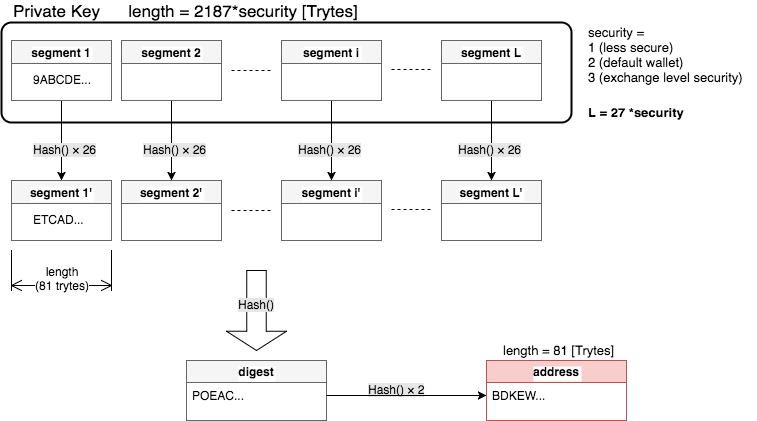
①　シードから生成されるPrivate Keyを用意する。
②　Private Keyを27個のセグメントに分割し、それぞれのセグメントごとを26回ハッシュ関数に通す。（'L'は最後のセグメントのインデックス。）L = security * 27。
③　②で生成されたすべてのセグメントをまとめてハッシュ関数に通す。その結果得られた値をdigestと呼ぶ。
④　digestを2回ハッシュ関数に通す。その結果得られた値をアドレスと呼ぶ。

　Private keyはsecurityという引数に代入した1~3の整数の値によって長さを変えることができる。（一応4以上も設計上可能であるが、その分Bundleの署名部分が長くなり、Tangleとのデータ通信効率が悪くなる。詳細）

#署名の方法
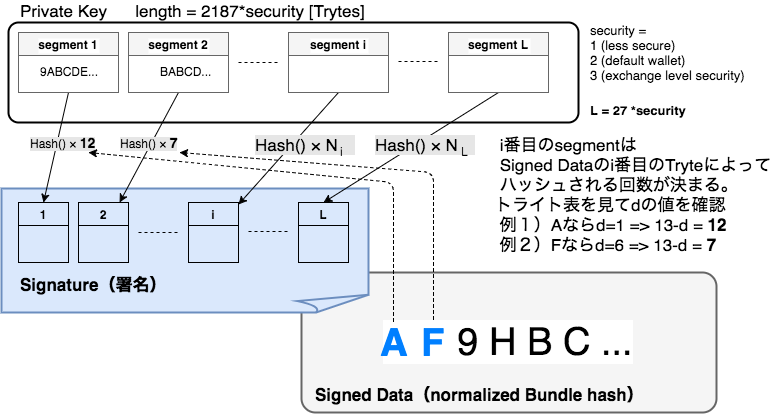
①　Private Keyを（アドレス生成と同じやり方で）27個のセグメントに分割する。
②　セグメントごとにN回分ハッシュ関数に通す。

Nの求め方
**署名されるデータ（Signed Data）**のi番目のTryteを見る（A〜Zか9、の全27種類）そのTryteがこの表のdecimalのどの数字dに対応しているか確認する。（9ならd=0、Aならd=1...Mならd=13、Nならd=-13...Yならd=-2、Zならd=-1）
Ni = 13 - d
i番目のセグメントをNi回ハッシュ関数に通す。

③　そのようにしてハッシュ関数で置き換えられたセグメントたちを順番に横に並べたものをSignature（署名）とする。

#承認の方法（アドレスの逆生成）
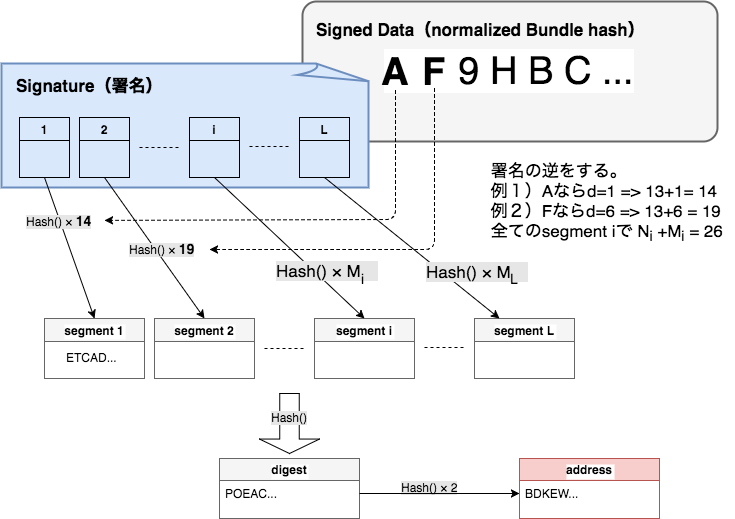
①　署名を（アドレス生成と同じやり方で）27個のセグメントに分割する。
②　セグメントごとにM回分ハッシュ関数に通す。

Mの求め方（基本的にNと類似）
署名されたデータ（Signed Data）のi番目のTryteを見る（A〜Zか9、の全27種類）そのTryteがこの表のdecimalのどの数字dに対応しているか確認する。（9ならd=0、Aならd=1...Mならd=13、Nならd=-13...Yならd=-2、Zならd=-1）
Mi = 13+d
i番目のセグメントをMi回ハッシュ関数に通す。

③　②で生成されたすべてのセグメントをまとめてハッシュ関数に通す。その結果得られた値をdigestと呼ぶ。
④　digestを2回ハッシュ関数に通す。その結果得られた値がアドレスと一致したら承認される。

署名されるデータ（Signed Data）

　IOTAの署名はこの記事でも説明した通り、入力部の生成で必要となったことを思い出して欲しい。Signed DataをPrivate Keyで署名し、署名は入力部のsignatureFragmentに保管される。では、その*Signed Data（署名されるデータ）*は何に当たるのかを最後に説明したい。
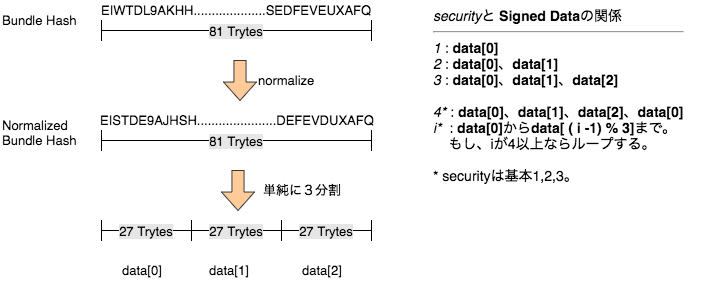
　それは、**Bundleのハッシュ（81トライト）**である。（厳密にいうとBundleのハッシュを少々ずらしたNormalized Bundleと呼ばれる中間生成物である。Normalized Bundleも81トライトの文字列でほぼBundleハッシュとして扱えるので細かい話は後に回す。）

　*Signed Data（署名されるデータ）*は上図のように、data[0]、data[1]、data[2]というNormalized Bundleを分割したものを使う。27セグメントを何回ハッシュに通すかはSigned Dataの27トライトに対応していた。この27トライトが上図のdata[i]である。securityとの関係だが、securityレベルによってPrivate keyの長さ（= security * 2187）は変化し、それによってセグメントの数（=security*27）が変化したことを思い出してほしい。security=2の場合、セグメント数は54個、つまりdata[0]とdata[1]合わせた54トライトと対応させてセグメントを一つずつN回ハッシュにかける。（Nの求め方は上で説明した。）
　Bundle生成の話と繋げる。securityによって署名の数が増えた理由は、署名①はdata[0]、署名②はdata[1]、という風に署名されるデータの分担を行なっていたからである。

デフォルトのAPIでは発行できないが理論上、securityが4以上もTangleで承認される。（マルチシグはその特性を利用する）。その際はNormalized Bundleが81トライトという理由で、data[2]の次はdata[0]という風にループさせて署名されるデータを作る。

##Normalized Bundleの生成
　口では説明し難いのでソースコードにコメントをふった。マニアックすぎるので正直言って無視して良い。
　なるべくトライト表の両端にあるアルファベット（ABCやXYZ）を中間方面（...IJKL...）へ寄せバランスを取らせている。これは後述するアドレス再利用の際のリスクを軽減させる作用がある。

Bundle.java

/**
     * Normalized the bundle.
     * return the bundle each tryte is written in integer[-13~13]
     *
     * @param bundleHash BundleのHash。
     * @return normalizedBundle A normalized bundle hash.
     */
    public int[] normalizedBundle(String bundleHash) {

        //  normalized Bundle 81トライト。
        //  これに値を当てはめてreturnする。
        int[] normalizedBundle = new int[81];

        //  Bundle Hash(81 トライト)を３つのセクションに分割(1つあたり27トライト)
        for (int i = 0; i < 3; i++) {

            // sum セクションの合計。
            long sum = 0;

            //  1セクション内を１トライトずつ確認し、
            //  そのトライトに対応する整数[-13~13]を求めてセクションの合計に加えていく。
            for (int j = 0; j < 27; j++) {

                //  sum += value
                //  value = normalizedBundleのi*27+j番目のトライト[9~Z]を数字[-13~13]に変換
                sum += 
                    //  トライトに対応する整数[-13~13]をnormalizedBundleの該当ポジションに代入。
                    (normalizedBundle[i * 27 + j] = 

                        //  トライト[9ABC...Z]を整数[-13~13]に変換
                        Converter.value(Converter.tritsString("" + bundleHash.charAt(i * 27 + j)))
                    );
            }

            // もし、sumが0以上なら、
            if (sum >= 0) {

                //  sumが0になるまで
                while (sum-- > 0) {

                    //  セクション内で[-13]以上のトライトを-1する。一つ-1したら最初から。
                    for (int j = 0; j < 27; j++) {
                        if (normalizedBundle[i * 27 + j] > -13) {
                            normalizedBundle[i * 27 + j]--;
                            break;
                        }
                    }
                }

            //  もし、sumが0以下なら、
            } else {

                //  sumが0になるまで
                while (sum++ < 0) {

                    //  セクション内で[13]以下のトライトを+1する。一つ+1したら最初から。
                    for (int j = 0; j < 27; j++) {

                        if (normalizedBundle[i * 27 + j] < 13) {
                            normalizedBundle[i * 27 + j]++;
                            break;
                        }
                    }
                }
            }
        }

        return normalizedBundle;
    }

#アドレス再利用のリスク
　基本的にIOTAのアドレスは再利用できない。
　言い換えると、一度支払い元として使ったアドレスに入金できない。
　厳密に言うと、一度入力アドレスとして使ったアドレスはもう一度入力アドレスとして使ってはならない。
　もっと厳密に言うと、一度署名に使ったPrivate Keyを別の署名に使わない。

　何故こうなるのかというと、2回目に署名されるデータによっては、Private Key内の複数のセグメントにおいて、2回目の署名時に行うハッシュ回数$N_2$が1回目に行ったハッシュ回数$N_1$より大きくなり、1回目の署名からその部分だけ$N_2-N_1$回分少なくハッシュにかければ、その部分だけ2回目の署名を生成することができてしまう。先ほど複数という風に表現したが、確率的には50%のセグメントにおいて2回目の署名が誰にでも可能になる。
　言い換えると1回目に署名されたトライトの場所が、2回目署名時にそれ以上（ここで言うトライトの大小は小さい方から9ABC...XYZである）のトライトがある場所だった場合、1回目の署名からその場所を抜き出して、足りないハッシュ回数分、ハッシュの続きを行うことで、古い署名から新しい署名をそのトライトの部位においては作り出せる。もう一度言うと、この部分は全体の約50%（security=1なら約13トライトのBundleハッシュ分）になるはずだ。（50% = 署名されるデータ内のある場所において、1回目より2回目のトライトの方が大きくなる確率）
　前の章でBundleハッシュをNormalizeしたのは、なるべくBundleハッシュ内の9やA,B,Cなどのハッシュ回数が少なくなるトライトを大きい数字に変えることでPrivate Keyが再利用された時に少しでもPrivate Key露出率を50%から下げるためである。

　技術的なことが分からなくても、とりあえずIOTAで送金をするたびに、ウォレットの"受取"のところからアドレスを生成するだけで防げるが実はここに盲点がある。スナップショット後はアドレス使用履歴がホストノード上のTangleでは消去されるが、Permanodeには残っている。
　アドレスを生成した後は必ずTangle Explorerなどでそのアドレスを検索して以前使われた（負の額のtxが存在する）かどうかを最終確認する。

量子計算耐性

　この署名方式を採択した背景には量子コンピュータ耐性を持たせると言う目的がある。IOTAが採用した署名はWOTS署名と呼ばれる。これについてはWinternitz one-time signatureという論文がある。また、このWOTS署名のアイデアの元となったランポート署名については、量子コンピュータ耐性があるランポート署名について解説&シェルスクリプトで実装してみたという記事が参考になるかもしれない。

#トライト表

#参考文献
IOTA公式ライブラリ https://github.com/iotaledger
本記事はSigningという部分。JavaScriptならsigning.js、JavaならSigning.javaから。

　IOTAの公式Slackに参加お待ちしております。また、本記事の間違いなどは、コメント欄でもTwitterからでもご報告いただけると幸いです。