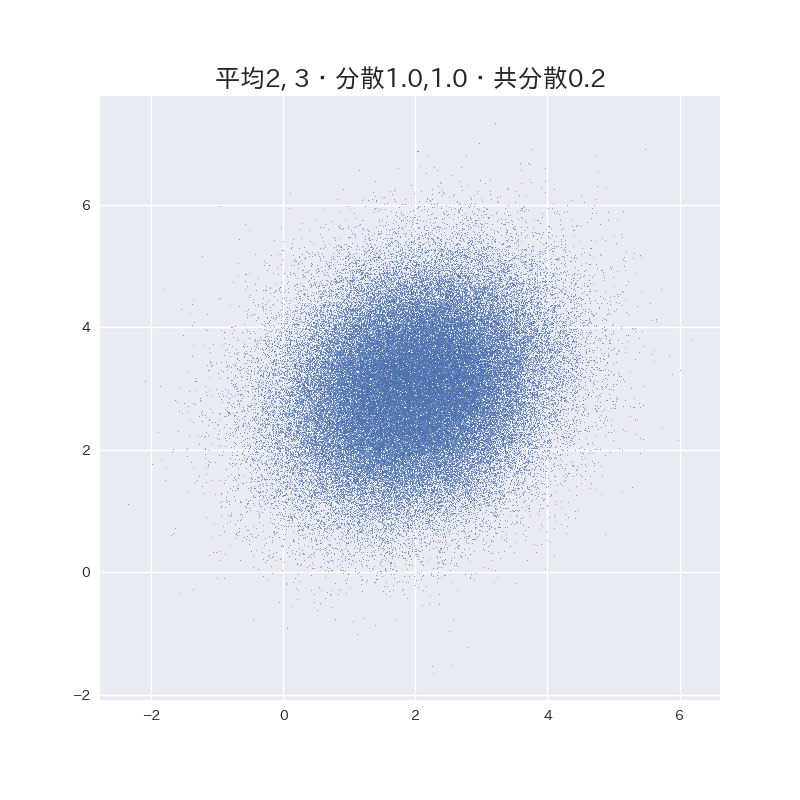
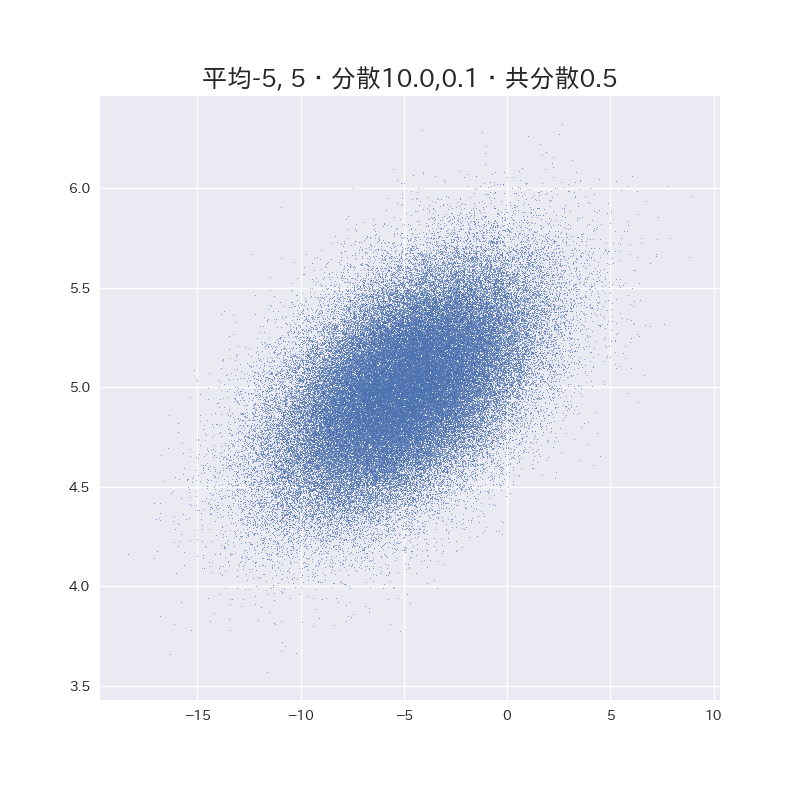
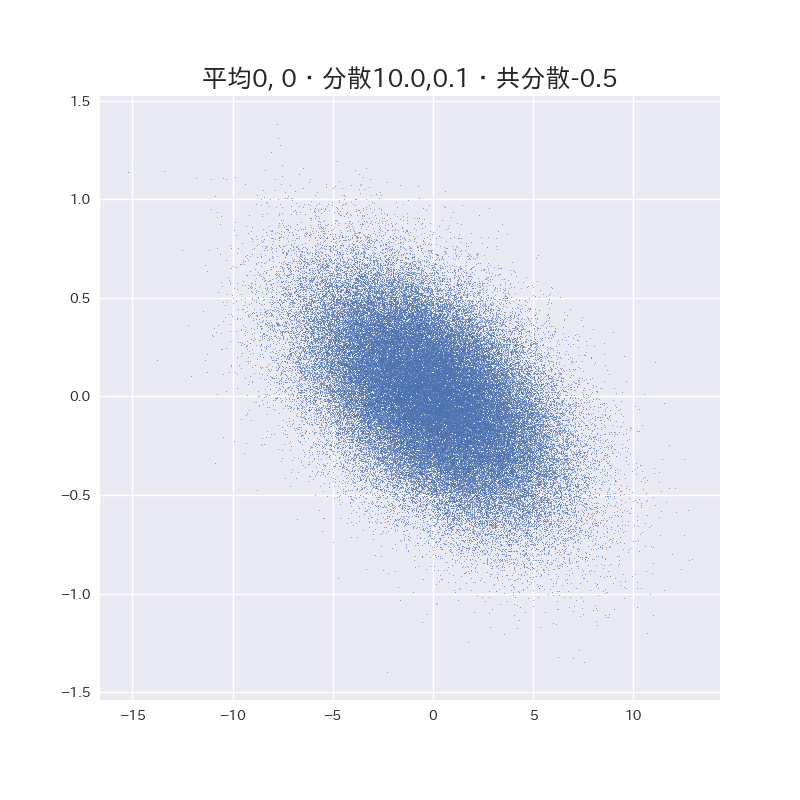
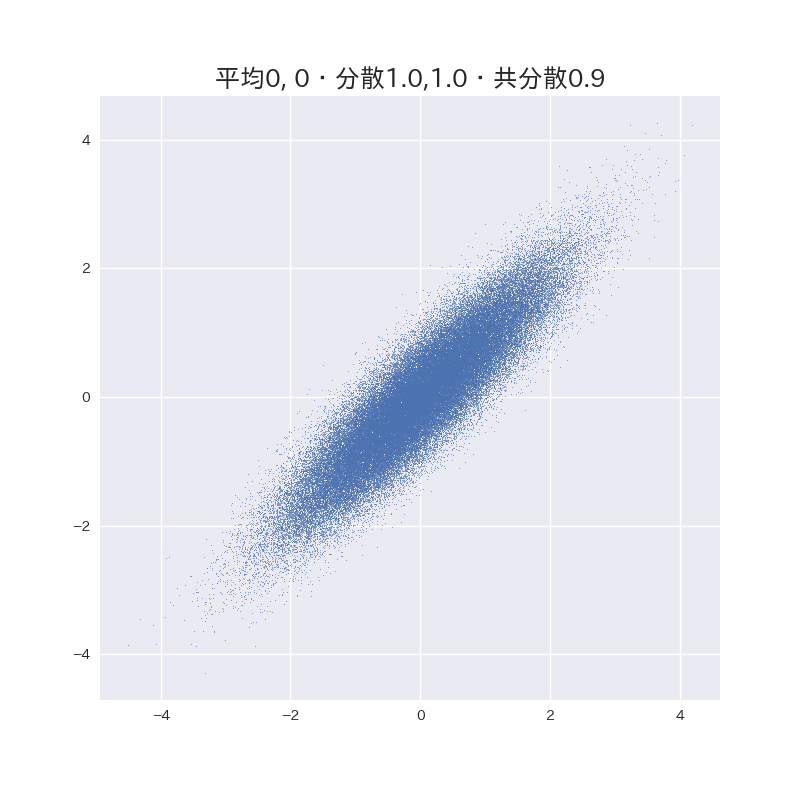
金融界隈で定量的な分析やデータサイエンスをやっている9uantです.
twitterもやってるので,興味ある方はぜひフォローしていただけると!
分散共分散行列のChoresky分解で、独立な標準正規分布に従う乱数を、多変量正規分布に従う乱数に変換できる。
どゆこと?
1. 数学的背景
- 確率変数の変数変換
- 多次元正規分布の導出
- 分散共分散行列の性質
- Cholesky分解のアルゴリズム
を解説する。
1.1. 多次元確率分布の変数変換
確率変数
\begin{eqnarray}
X_1,\ X_2,\ \cdots ,\ X_n
\end{eqnarray}
を、確率変数
\begin{eqnarray}
Y_1,\ Y_2,\ \cdots ,\ Y_n
\end{eqnarray}
に変換する。
ただし、$X$と$Y$は、それぞれ
\begin{eqnarray}
&f_X&\left(x_1,\ x_2,\ \cdots ,\ x_n\right)\\
&f_Y&\left(y_1,\ y_2,\ \cdots ,\ y_n\right)
\end{eqnarray}
の確率密度関数をもつものとする。
各$Y$を、$X$の全単射として、
\begin{eqnarray}
\begin{cases}
Y_1 = h_1\left(X_1,\ X_2,\ \cdots ,\ X_n\right)&\\
Y_2 = h_2\left(X_1,\ X_2,\ \cdots ,\ X_n\right)&\\
\ \vdots &\\
Y_n = h_n\left(X_1,\ X_2,\ \cdots ,\ X_n\right)
\end{cases}
\end{eqnarray}
と表す。各$h_i$は全単射ゆえ逆関数が存在し、
\begin{eqnarray}
\begin{cases}
X_1 = g_1\left(Y_1,\ Y_2,\ \cdots ,\ Y_n\right)&\\
X_2 = g_2\left(Y_1,\ Y_2,\ \cdots ,\ Y_n\right)&\\
\ \vdots &\\
X_n = g_n\left(Y_1,\ Y_2,\ \cdots ,\ Y_n\right)
\end{cases}
\end{eqnarray}
と表される。$n$次元実数空間の任意の部分集合$D$に対して、積分の変数変換を施して、
\begin{eqnarray}
&\int\cdots\int_D& f_X\left(x_1,x_2,\cdots ,x_n\right) dx_1dx_2\cdots dx_n \nonumber \\
= &\int\cdots\int_D& f_X\left(y_1,y_2,\cdots ,y_n\right)\left|\frac{\partial\left( x_1,x_2,\cdots x_n\right) }{\partial\left(y_1,y_2,\cdots y_n\right) }\right| dy_1dy_2\cdots dy_n
\end{eqnarray}
が成立する。
ただし、ヤコビアンを、
\begin{eqnarray}
\left|\frac{\partial\left( x_1,x_2,\cdots x_n\right) }{\partial\left(y_1,y_2,\cdots y_n\right) }\right| =
\begin{pmatrix}
\frac{\partial g_1}{\partial y_1}&\frac{\partial g_1}{\partial y_2}&\cdots&\frac{\partial g_1}{\partial y_n}\\
\frac{\partial g_2}{\partial y_1}&\ddots&&\vdots\\
\vdots &&\ddots&\vdots\\
\frac{\partial g_n}{\partial y_1}&\cdots&\cdots&\frac{\partial g_n}{\partial y_n}
\end{pmatrix}
\end{eqnarray}
と表記している。
ここから、確率密度関数の変換式
\begin{eqnarray}
f_Y\left(y_1,y_2,\cdots ,y_n\right)
= f_X\left(y_1,y_2,\cdots ,y_n\right)\left|\frac{\partial\left( x_1,x_2,\cdots x_n\right) }{\partial\left(y_1,y_2,\cdots y_n\right) }\right|
\end{eqnarray}
を得る。
1.2. 多次元正規分布の導出
$1$次元標準正規分布を、$N\left(0,1\right)$と表記する。
互いに独立な$n$個の標準正規分布
\begin{eqnarray}
Z_1,\ Z_2,\cdots ,\ Z_n \sim N\left(0,1\right)\ \textrm{i.i.d}
\end{eqnarray}
を定める。
これらの同時密度関数は、独立分布であるため積で表され、
\begin{eqnarray}
f_Z\left(z\right) = \frac{1}{\left(2\pi\right)^{n/2}} \exp\left(-\frac{1}{2}z^Tz\right)
\end{eqnarray}
となる。
ここで、
\begin{eqnarray}
X &=& AZ + \mu
\end{eqnarray}
の変数変換を施す。
ただし、$Z,X$は$n$次元確率変数ベクトル、$A$は$n\times n$行列、$\mu$は$n$次元ベクトルである。
\begin{eqnarray}
X&=&\left(X_1,\ X_2,\ \cdots\ X_n\right)^{\mathrm{T}} \nonumber \\
Z&=&\left(Z_1,\ Z_2,\ \cdots\ Z_n\right)^{\mathrm{T}} \nonumber \\
A&=&
\begin{pmatrix}
a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\
a_{2,2}&\ddots&&\vdots\\
\vdots&&\ddots&\vdots\\
a_{n,1}&\cdots&\cdots&a_{n,n}
\end{pmatrix} \nonumber \\
\mu&=&\left(\mu_1,\ \mu_2,\ \cdots\ \mu_n\right)^{\mathrm{T}} \nonumber
\end{eqnarray}
変数変換のヤコビアンは、
\begin{eqnarray}
\left|\frac{\partial\left( x_1,x_2,\cdots x_n\right) }{\partial\left(z_1,z_2,\cdots z_n\right) }\right| &=& \det\left( A\right)
\end{eqnarray}
より、
\begin{eqnarray}
\left|\frac{\partial\left( z_1,z_2,\cdots z_n\right) }{\partial\left(x_1,x_2,\cdots x_n\right) }\right| &=& \frac{1}{\det\left( A\right)}
\end{eqnarray}
を得る。
よって、$X$の同時密度関数は、
\begin{eqnarray}
f_X\left(x\right)&=&f_Z\left(A^{\mathrm{T}}\left(x-\mu\right)\right)\frac{1}{\det\left(A\right)} \nonumber \\
&=&\frac{1}{\left(2\pi\right)^{n/2}\det\left(A\right)}\exp\left\{-\frac{1}{2}\left(x-\mu\right)^{\mathrm{T}}AA^{\mathrm{T}}\left(x-\mu\right)\right\}
\end{eqnarray}
となる。
変換された確率変数の平均ベクトルと、分散共分散行列は、
\begin{eqnarray}
E\left[X\right]&=&AE\left[Z\right]+\mu \nonumber \\
&=&\mu
\\
Cov\left(X\right)&=&E\left[\left(X-\mu\right)\left(X-\mu\right)^{\mathrm{T}}\right] \nonumber \\
&=&E\left[AZZ^{\mathrm{T}}A^{\mathrm{T}}\right] \nonumber \\
&=&AE\left[Z\right] E\left[Z^{\mathrm{T}}\right] A^{\mathrm{T}} \nonumber \\
&=&AA^{\mathrm{T}}
\end{eqnarray}
分散共分散行列を、
\begin{eqnarray}
\Sigma = AA^{\mathrm{T}}
\end{eqnarray}
と表記する。
これを適用して、多次元正規分布の同時密度関数
\begin{eqnarray}
f_X\left(x\right)
&=&\frac{1}{\left(2\pi\right)^{n/2}\det\left(A\right)}\exp\left\{-\frac{1}{2}\left(x-\mu\right)^{\mathrm{T}}\left(AA^{\mathrm{T}}\right)^{-1}\left(x-\mu\right)\right\} \nonumber \\
&=&\frac{1}{\left(2\pi\right)^{n/2}\det\left(\Sigma\right)^{1/2}}\exp\left\{-\frac{1}{2}\left(x-\mu\right)^{\mathrm{T}}\Sigma^{-1}\left(x-\mu\right)\right\}
\end{eqnarray}
を得る。
1.3. 分散共分散行列の性質
分散共分散行列からCholesky分解によって乱数列を生成するにあたり、分散共分散行列が正定値であるという制約条件が必要になる。
ここでは、一般に分散共分散行列の性質を確認し、Cholesky分解可能性を確かめる。
ここで、線形代数の知識を確認する。
行列の半正定値性
以下は同値。
- $n\times n$対称行列$A$が半正定値である
- 任意のベクトル$x$に対して、$x^\mathrm{T}Ax\geq 0$
- $A$の任意の主小行列式が非負
- 全ての固有値は非負
行列の正定値性
以下は同値。
- $n\times n$対称行列$A$が正定値である
- 任意のベクトル$x$に対して、$x^\mathrm{T}Ax> 0$
- $A$の任意の主小行列式が正
- 全ての固有値は正
以下の主張を証明する。
分散共分散行列$\Sigma$は半正定値対称行列である。
分散$\sigma_i$、共分散$\rho_{i,j}$を成分とする$n\times n$分散共分散行列を$\Sigma$とする。
$\rho_{i,j}=\rho_{j,i}$より、$\Sigma$は対称行列である。
$a$を任意の$n$次元定数ベクトルとする。
\begin{eqnarray}
a^{\mathrm{T}}\Sigma a &=& a^{\mathrm{T}}E\left[\left(X-E\left[X\right]\right)\left(X-E\left[X\right]\right)^{\mathrm{T}}\right]a \nonumber \
&=&E\left[a^{\mathrm{T}}\left(X-E\left[X\right]\right)\left(X-E\left[X\right]\right)^{\mathrm{T}}a\right] \nonumber \
&=&E\left[\langle a,X-E\left[X\right]\rangle^2\right] \nonumber \
&\geq&0 \nonumber
\end{eqnarray}
>よって、$\Sigma$は半正定値である。
実用上、分散共分散行列は多くの場合で正定値対称となることが期待されるが、
正定値対称とならない場合は、以下の乱数生成ができないため注意。
## 1.4. Cholesky分解
正定値対称行列$A$に対して、下三角行列$L$を用いて分解を与えることを、Cholesky分解という。
```math
\begin{eqnarray}
A&=&LL^{\mathrm{T}}
\\
\nonumber \\
A&=&
\begin{pmatrix}
a_{1,1}&a_{1,2}&\cdots&a_{1,n}\\
a_{2,2}&\ddots&&\vdots\\
\vdots&&\ddots&\vdots\\
a_{n,1}&\cdots&\cdots&a_{n,n}
\end{pmatrix} \nonumber \\
L&=&
\begin{pmatrix}
l_{1,1}&0&\cdots&\cdots&0\\
l_{2,1}&l_{2,2}&0&&\vdots\\
\vdots&&\ddots&\ddots&\vdots\\
\vdots&&&l_{n-1,n-1}&0\\
l_{n,1}&\cdots&\cdots&l_{n,n-1}&l_{n,n}
\end{pmatrix} \nonumber
\end{eqnarray}
Cholesky分解の構成法は、以下の通りである。
\begin{eqnarray}
l_{i,i}&=&\sqrt{a_{i,i}-\sum_{k=1}^{i-1}l_{i,k}^2}\ \ \ \ \ \ \left(\textrm{for}\ i=1,\cdots ,n\right) \\
l_{j,i}&=&\left(a_{j,i}-\sum_{k=1}^{i-1}l_{j,k}\ l_{i,k}\right)/l_{i,i}\ \ \ \left(\textrm{for}\ j=i+1,\cdots ,n\right)
\end{eqnarray}
1.5. Cholesky分解による多変量正規分布に従う乱数列の生成
分散$\sigma_i$、共分散$\rho_{i,j}$を成分とする分散共分散行列$\Sigma$に対し、正定値の制約を設ける。
$\Sigma$に対してCholesky分解を適用して、$A=L$(下三角行列)を得る。
\begin{eqnarray}
x&=&Lz+\mu \\
\nonumber \\
L&=&
\begin{pmatrix}
l_{1,1}&0&\cdots&\cdots&0\\
l_{2,1}&l_{2,2}&0&&\vdots\\
\vdots&&\ddots&\ddots&\vdots\\
\vdots&&&l_{n-1,n-1}&0\\
l_{n,1}&\cdots&\cdots&l_{n,n-1}&l_{n,n}
\end{pmatrix} \nonumber \\
l_{i,i}&=&\sqrt{\sigma_{i}-\sum_{k=1}^{i-1}l_{i,k}^2}\ \ \ \ \ \ \left(\textrm{for}\ i=1,\cdots ,n\right) \nonumber \\
l_{j,i}&=&\left(\rho_{j,i}-\sum_{k=1}^{i-1}l_{j,k}\ l_{i,k}\right)/l_{i,i}\ \ \ \left(\textrm{for}\ j=i+1,\cdots ,n\right) \nonumber
\end{eqnarray}
2. 実装
import numpy as np
# 平均
mu = np.array([[2],
[3]])
# 分散共分散行列
cov = np.array([[1,0.2],
0.2,1]])
L = np.linalg.cholesky(cov)
dim = len(cov)
random_list=[]
for i in range(n):
z = np.random.randn(dim,1)
random_list.append((np.dot(L,z)+mu).reshape(1,-1).tolist()[0])