層の定義の復習
位相空間 $X$ の上の 前層(presheaf) $F$ とは関手
$$ F: \mathcal{O}^{\mathrm{op}}_X \rightarrow \mathrm{Set}$$
の事である。
$F$ が $\mathcal{O}_X^{\mathrm{op}}$ の任意の余完備充満部分圏 $J$ について極限を保つ時、これを 層(sheaf) と言う。
$$ F(\lim_{\leftarrow}J) \simeq \lim_{\leftarrow}F(J) $$
極限錐の様子
$F$ が前層のとき、極限錐(cone) の様子を図示すると下図のようになる。ここで気をつけたいのは、 $F(J)$ の中の射は $J$ の包含関係を $F$ で移したものだから定義より制限射だが、側面にある射(青い部分)は定義上は制限射であるとは限らない。しかし、$F$ が極限を保存する場合にはcone全体を $F$ で写し取ったものもconeになるので、側面部分が制限射であるとして良い。
「して良い」というのは、$\lim F(J)$は複数存在し得るが、極限の性質としてそれらは必ず互いに同型なのだから、具体的に頂点が $F(\lim J)$ で側面の射が制限射であるconeを用いても矛盾なく議論が進められるという事。
極限の図式
$F$ が層である条件を図式で書くと以下のようになる。
$J$ を $\mathcal{O}_X^{\mathrm{op}}$ のcocomplete full subcategoryとし、その対象の集合を $\{U_\lambda\}$ とする。また$U=\lim_{\leftarrow}J = \bigcup U_\lambda$ と書く。
$F$ が層であるとは、全ての$\alpha,\beta$に対して以下の図式を可換にする、任意の対象 $G\in\mathrm{Set}$ と射の族 $\{f_\lambda:G\rightarrow F(U_\lambda)\}$ に対して、全ての $\alpha,\beta$ に対して以下の図式を可換にする $u: G\rightarrow F(U)$ が唯一つ存在することである。

一般的な定義との同値性
まず前層の一般的な定義は以下のようになる。
位相空間 $X$ の各開集合に集合を対応させる集合 $F$ について、任意の開集合 $U\supset V$について写像 $r^U_V: F(U)\rightarrow F(V)$ が存在し以下を満たす時、これを前層という。
- $r^U_U = \mathrm{id}_U$
- $U\supset V\supset W$ の時 $r^V_W\circ r^U_V = r^U_W$
$r^U_V$ を制限写像とよび、以下のように表記する。
$$ r^U_V: F(U)\ni f \longmapsto f|_V \in F(V)$$
また $F(U)$ の元を切断と呼ぶ。
これは $(F, r)$ が関手であるということそのものである。続いて、これが層となる条件は次のようなものである。
前層 $(F, r)$ が層であるとは、任意の開集合 $U$ とその開被覆 $U=\bigcup U_\lambda$ に対して、以下が成り立つものである。
切断の族 $\{s_\lambda \in F(U_\lambda)\}$ が全ての $U_\alpha,U_\beta$ について$s_\alpha|_{U_\alpha\cap U_\beta}=s_\beta|_{U_\alpha\cap U_\beta}$であるならば、全ての $U_\lambda$ に対して $s|_{U_\lambda}=s_\lambda$ となる $s\in F(U)$ が一意に存在する。
これが圏論的定義と一致するのかどうかはパッと見では難しいだろうから証明をする。
一般的な定義⇨圏論的定義
$(F, r)$ が一般的な定義の元で層になるとする。
$J$ を $\mathcal{O}_X^{\mathrm{op}}$ のcocomplete full subcategoryとし、その対象の集合を $\{U_\lambda\}$ とする。また$U=\lim_{\leftarrow}J = \bigcup U_\lambda$ と書く。集合 $G\in\mathrm{Set}$ と射の族 $\{f_{U_\lambda}:G\rightarrow F(U_\lambda)\}$ を以下の図式を全ての $U_\alpha,U_\beta\in J$ について可換にするものとする。

ここで $x\in G$ に対して $f_{U_\lambda}(x)=s_{U_\lambda}$ とおく。任意の $U_\alpha,U_\beta\in J$ について $J$ はcocompleteだから $U_{\alpha\cap\beta}\in J$ であるので、上の図式には以下のようなものも含まれ
$$ s_{U_\alpha}|_{U_\alpha\cap U_\beta}=s_{U_\alpha\cap U_\beta}$$

同様にして $ s_{U_\beta}|_{U_\alpha\cap U_\beta}=s_{U_\alpha\cap U_\beta}$。従って全ての$U_\alpha,U_\beta$について
$$ s_{U_\alpha}|_{U_\alpha\cap U_\beta}=s_{U_\beta}|_{U_\alpha\cap U_\beta}$$
であるから、全ての $U_\lambda$ に対して $ s_x|_{U_\lambda}=s_{U_\lambda} $ を満たす $s_x\in F(U)$ が一意に存在する。この $s_x$ を用いて $u: G\rightarrow F(U)$ を
$$ u(x) = s_x $$
と定めると以下の図式が全ての $\alpha,\beta$ に対して可換となる $u$ が一意に得られる。(証明終)

集合の層でない場合
以上の定義は $\mathrm{Set}$に値をもつ層の場合の証明であるが、加群の層やアーベル群の層などの場合には $u$ が準同型である事も加えて示す必要があるので注意。証明自体は $f_{U_\alpha}$ が準同型であることから簡単に出来る。
圏論的定義⇨一般的な定義
関手 $F:\mathcal{O}_x^{\mathrm{op}}\rightarrow\mathrm{Set}$ が圏論的な層の定義を満たすとする。開集合 $U$ とその開被覆 $U=\bigcup U_\lambda$ を取る。 $J$ を $\{U_\lambda\}$ の有限個の集合($0$ 個を含む)の共通部分とその間の射からなる圏とするとするとこれは $\mathcal{O}_x^{\mathrm{op}}$の余完備充満部分圏となる。以後、開被覆の要素を $U_\lambda$、$J$ の対象を $U'_{\mu}$ と表記する。
切断の族 $\{s_\lambda \in F(U_\lambda)\}$ が全ての $U_\alpha,U_\beta$ について$s_\alpha|_{U_\alpha\cap U_\beta}=s_\beta|_{U_\alpha\cap U_\beta}$であるとすると以下が成り立つ。
A: 任意の $U'_\mu$ について $U_\lambda\supset U'_\mu$ となる $U_\lambda$ が存在。
B: $U_\lambda\supset U'_\mu$ となる全ての $U_\lambda$ について $s_\lambda|_{U'_\mu}$は等しい。
Aは $J$ の構成より明らか。$U_{\alpha},U_{\beta}$ が $U'_\mu$ を含むとすると $U_\alpha\cap U_\beta\supset U'_\mu$ であるので$s_\alpha|_{U_\alpha\cap U_\beta}=s_\beta|_{U_\alpha\cap U_\beta}$ から $s_\alpha|_{U'_\mu}=s_\beta|_{U'_\mu}$ が得られる。これが任意の $\alpha,\beta$ で成立するのでBが示される。
そこで、射の族$\{f_{\mu}:1\rightarrow F(U'_{\mu})\}$ を以下のように構成する。
$$ f_{\mu}: 1\ni\star \longmapsto s_\lambda|_{U'_\mu} \in F(U'_\mu)$$
ここで $\lambda$ は $U_\lambda \supset U'_\mu$ であるものを取る。A,Bよりそのような $\lambda$ が存在することと、選び方によらないことが示される。
そうすると下のような図式が全ての $\alpha,\beta$ について可換である事が示されるので、以下の図式を可換にする $u$ が一意に存在する。
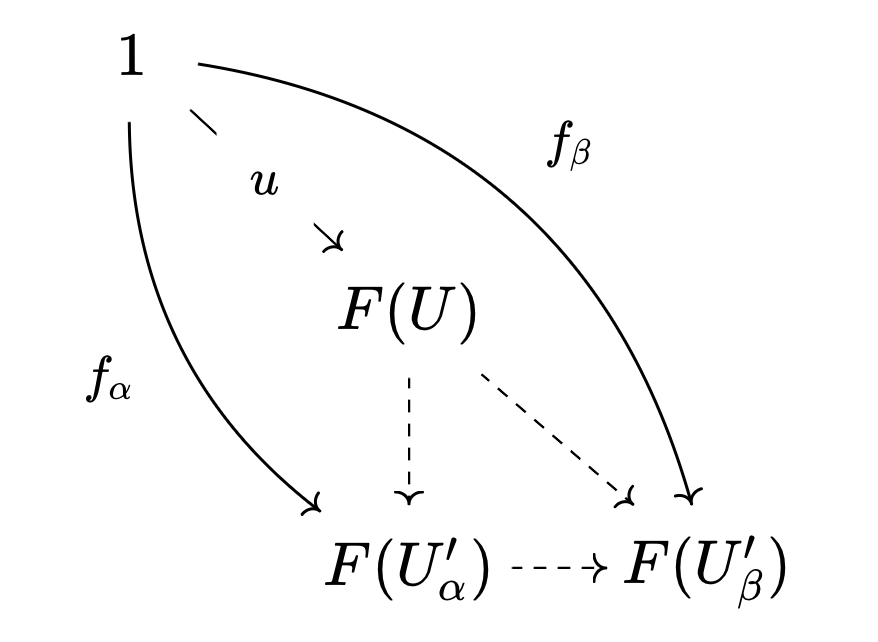
そこで $s=u(\star)$ とおく。すると任意の $U_\lambda$ について、 $U_\lambda$ も $J$ の対象であることと $U_\lambda\supset U_\lambda$ であることに注意すると
$$ 1\ni\star\longmapsto s_\lambda\in F(U_\lambda) $$
という射もconeに含まれているので、図式の可換性から $s|_{U_\lambda}=s_\lambda$ が成立。(証明終)
集合の層でない場合
加群の層やアーベル群の層などの場合には以下の射の構成はできない。
$$ f_{\mu}: 1\ni\star \longmapsto s_\lambda|_{U'_\mu} \in F(U'_\mu)$$
何故ならば、$f_\mu$ は準同型でなければならないから。ここでどうするしばらく悩んだが、$1$ の代わりに $(s_\lambda|_{U'_\mu})_\mu$ が生成するアーベル群だったり、加群をとり、 $f_\mu$ を $\mu$ 番目を取り出す射影と包含写像の合成射とすれば良い。(もっと綺麗な証明方法があったらどなたか教えてください)
