追記: 2017/06/06
その後の成果
その後の私達の努力の結果、下記記事のコードよりさらに高速化されています。近日sgemmのコードを公開する予定です。
また以下の記事ではraspiのgpuを活用する事で画像認識等が速くなるはずだという事を言いましたが、その後以下のような成果が出ています。ConvolutionやActivation等もGPU上で実行するようにしています。
Object recognition camera with GoogLeNet, a 1000-class image classification model, running locally on #RaspberryPi 3 pic.twitter.com/WP99ePpfrM
— 中村晃一 (@9_ties) 2017年4月29日
Raspberry Pi Zero version pic.twitter.com/5ALlnvFEe8
— 中村晃一 (@9_ties) 2017年4月29日
Raspberry Pi Advent Calendar 2015の投稿記事です。先日PyVideoCoreというRaspberry PiでGPGPUを行う為のPythonライブラリを開発しました。これを使って単精度の行列乗算(sgemm)を題材に、GPGPUのチュートリアルを書こうと思います。自分用の記録も兼ねているので無駄に長いです。すみません。
きっかけ
RaspiのGPUについて調べていたときに他の方が書いたsgemm実装を見つけました。
これのサンプルを試してみたところ、96x363行列と363x3025行列の積が大体0.27秒ほどとの結果が出ます。この計算では約2億回の浮動小数点数演算(105996000回の乗算と105415200回の加算)が行われるので、783Mflopsくらいの性能となります。CBLASのsgemmで同じ計算をすると15.4秒くらいとの結果が出て、こちらは13.7Mflopsですから60倍近くの高速化を達成しているということになります。
この結果は一見すごそうですが、Raspi GPUの理論性能は24Gflopsですから実は**理論性能の3%**しか出せていません。他の人が書いたFFT(公式サンプルとしてraspbianに収録)やまた別の人が書いたSHA256とかも見たんですがどれも全然性能が出ていませんでした。現状Rasperry PiとGPGPUで検索するとこれらの情報源しかヒットしないので、これはまずいと思い本記事を書くことにしました。
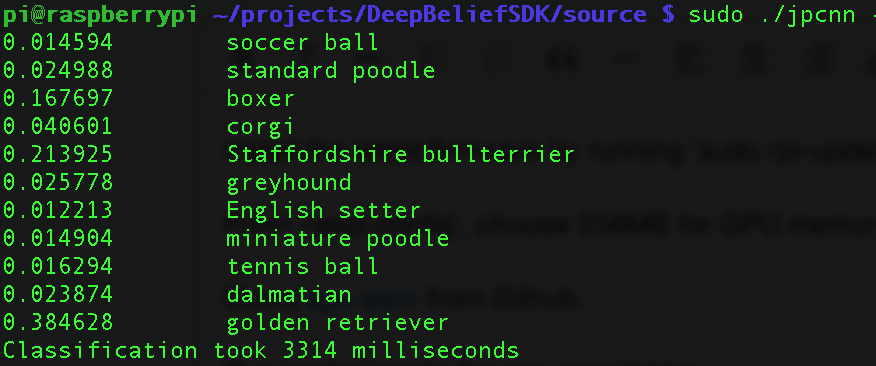
行列乗算が早くなって何が嬉しいのかと思うかもしれませんが、例えば上の人はpi-gemmを使ってDeepBeliefNetworkというモデルを使っての物体認識の高速化をしています。
これは、入力画像に何が写っているかを識別するものですが、sgemmをGPU化することで3.3秒で識別が出来るようになったそうです(上で言ったようにこれはまだまだ速く出来るはずです)。他にもgemmが速くなると嬉しい応用がたくさんあります。
学生にお勧め
Raspberry PiのGPUはVideoCore IVというものです。nVidiaのGPUのコードをアセンブリで書いた事のある人はそんなにいないと思いますが、VideoCoreの場合はアセンブリで書かなければならない書くことが出来ます。どの会社のGPUも基本的な考え方は同じですし、VideoCoreは完全なリファレンスガイドが公開されているし、ボードが安いですし、情報系学生の修行用にRaspi結構良いんじゃないでしょうか。
リファレンスガイド
VideoCoreは16-wayのSIMDプロセッサ(QPU)12個からなります。あとは説明を省略しますので、以下のリファレンスガイドを読んでください。穴が開くほど読んでください。
- http://www.broadcom.com/docs/support/videocore/VideoCoreIV-AG100-R.pdf
- https://docs.broadcom.com/docs/12358545
今回作るもの。
与えられた$p\times q$ 行列 $A$, $q\times r$ 行列 $B$, $p\times r$ 行列 $C$, スカラ $\alpha,\beta$に対して
$\alpha AB + \beta C$
を計算するというものを作ります。 結果は$C$に上書きします。
いわゆるsgemmですが、今回は大分単純化したものを作ります。
- 行列の転置等のオプションは作りません。
- Row-majorの場合のみを考えます。
- GPU側では$p$が16の倍数、$r$が64の倍数である事、を要請し端数処理を省きます。Host側で共有メモリに行列を配置する際に、端数部分の調整をする事にします。
- $q$は2以上であることを要請します。
速くする為に必要な事
性能を出すという問題は、つまり**如何に演算器を休ませずに走らせ続けられるか?**という問題です。その為には、出来るだけ演算器を数値計算の為に使う事、メモリアクセス、条件分岐、同期処理などでの待ち時間を減らす事、待ち時間が発生する場合にはパイプライン化やスレッド化でそれを隠蔽する事などが重要になります。
pi-gemmのアルゴリズムを例にこれを見てみましょう。pi-gemmでは内積計算の部分(以下のk-loop)をSIMDでベクトル化するという方法を採っています。CUDAのチュートリアルとかでも同様のサンプルを見かける事があります。
for i=0..p-1 {
for j=0..r-1 {
v = 0
for k=0..q-1 {
v += A[i, k]*B[k, j]
}
C[i, j] = α * v + β * C[i, j]
}
}
この場合
- 長さ16のベクトル2つA[i,k:k+16], B[k:k+16, j]をloadする。
- 2つのベクトルを掛けて、アキュムレータに足し込む。
という計算を繰り返す事になります。(いろいろ工夫できますが)これはあまり良くない方法だと思います。
RaspiのGPUは加算と乗算を同時に実行できるのでステップ2は実質1命令で終わります。ステップ1はこれよりずっと長い時間が掛かります。この間演算器は休んでいます。また、たった16個の数値を演算する毎に条件分岐があります。ここでも演算器は休んでいます。
実際のコードを引用すると、以下のようになっています。main_loop_l内部で実際の数値計算を行っているところはfmulとfadd1回ずつのみです。同時実行できるから実質1命令分です。その他はすべてアドレスやカウンタの計算です。ループ内14命令の内、数値演算の為には演算器を一回しか使えていません。1/14=7.1%ですから、先ほどの3%程度という数字になります。
main_loop_l:
# We read a pending A result from the queue, and then immediately fire off the
# next memory fetch, to get the maximum concurrency.
or.ldtmu0 ra39, ra39, ra39; nop
add raTmu0S, rCurrentA, rAccum1; nop
or rA0to15, r4, 0; nop
# Now we pull the values from B, and fire off the next fetch.
add.ldtmu1 rCurrentA, rCurrentA, rAccum2; nop
add raTmu1S, rCurrentB, rAccum1; nop
add rCurrentB, rCurrentB, rAccum2; fmul rAccum0, rA0to15, r4
fadd rTotal, rTotal, rAccum0; nop
sub rL, rL, -16; nop
sub rAccum0, rK, 15; nop
sub ra39, rL, rAccum0; nop
brr.ns ra39, main_loop_l
NOP
NOP
NOP
演算器だけでなくベクトルレジスタを上手く使うという事も大切です。レジスタを上手く使わないと、必然的にメモリに置くデータが増えます。メモリはレジスタより圧倒的に遅いです。
ベクトル計算機はレジスタを沢山搭載しているのが特徴で、VideoCoreの場合は各QPU毎に長さ16のレジスタが64本あります。つまり、各QPU上に最大16x64の行列(1024成分)を置くことができます。QPUは12個あるので全体では最大12288個の実数値を同時にレジスタ上に置く事が出来ます。pi-gemmのコードを見てみると64本中1本だけ(rTotal)が実数値用で他はアドレスとかループのインデックス用です。これは非常にもったいないです。
64本のレジスタ(ra0,ra1,...,ra31とrb0,rb1,...,rb31)の他に、更に高速なアキュムレータが4本(r0,r1,r2,r3)あります。レジスタへ書き込まれた値は次の次の命令まで読めませんが、アキュムレータだと次の命令で読めます。4本しかないので無駄遣いしないようにしましょう。
mov(ra0, 1) # ここでの書き込まれた値は
nop()
iadd(ra0, ra0, 2) # ここで初めて読める
mov(r0, 1) # アキュムレータだと
isub(r0, r0, 1) # 次の命令で読める
以後、これらの事に気を付けながら、3重ループの一番内側のコードを書いていきます。続きは次回です。
最内ループは最も実行される回数が多いので、演算の密度が重要です。
今回の方針
64本のレジスタ全部を行列を格納する為に使います。行列のアドレス、メモリアクセスのストライド、インデックス、行列のサイズ$p,q,r$等のデータを置くレジスタが無くなりますが頑張れば何とかなります。
上で説明した様に、2つのベクトル$\mathbf{a},\mathbf{b}$をloadした時に如何にたくさんの有効な演算を行えるかがポイントです。長さ$n$のベクトルの内積
$$ \mathbf{a}^T\mathbf{b}=a_0b_0+a_1b_1+\cdots+a_{n-1}b_{n-1} $$
では、2nワードのloadに対して$n$回の乗算と$n-1$回の加算とこれを次々足しこむ為の加算が1回で計$2n$回しか演算ができません。そこで内積ではなく長さ$m$のベクトルと$n$のベクトルの直積
\mathbf{a}\mathbf{b}^T = \begin{pmatrix}
a_0b_0 & a_0b_1 & \cdots & a_0b_{n-1} \\
a_1b_0 & a_1b_1 & \cdots & a_1b_{n-1} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m-1}b_0 & a_{m-1}b_1 & \cdots & a_{m-1}b_{n-1}
\end{pmatrix}
が計算単位となるようにアルゴリズムを作ります。こちらでは$m+n$ワードのloadに対して、$mn$回の乗算と足しこみの為の加算が$mn$回、計$2mn$回の演算が可能です。
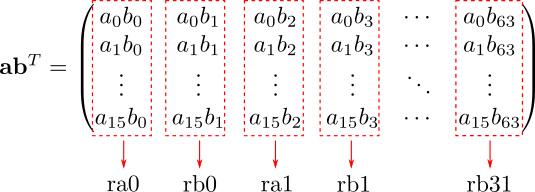
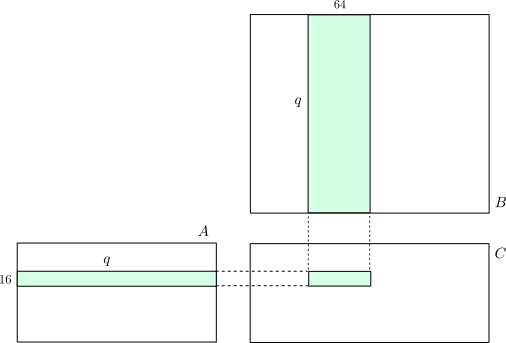
64個のレジスタの使い方ですが、下図のように16x64の行列を単位にして、乗算結果の各列ベクトルをレジスタに格納する事にします。32x32とか64x16にしなかった理由は後で説明します。
この掛け算をどうにかしてやって、次々足しこんでいけば下図の部分行列の積が計算できます。
これは伝統的な方法で、画像処理専用のGPUではαブレンドと加算合成を使って計算していたみたいです。
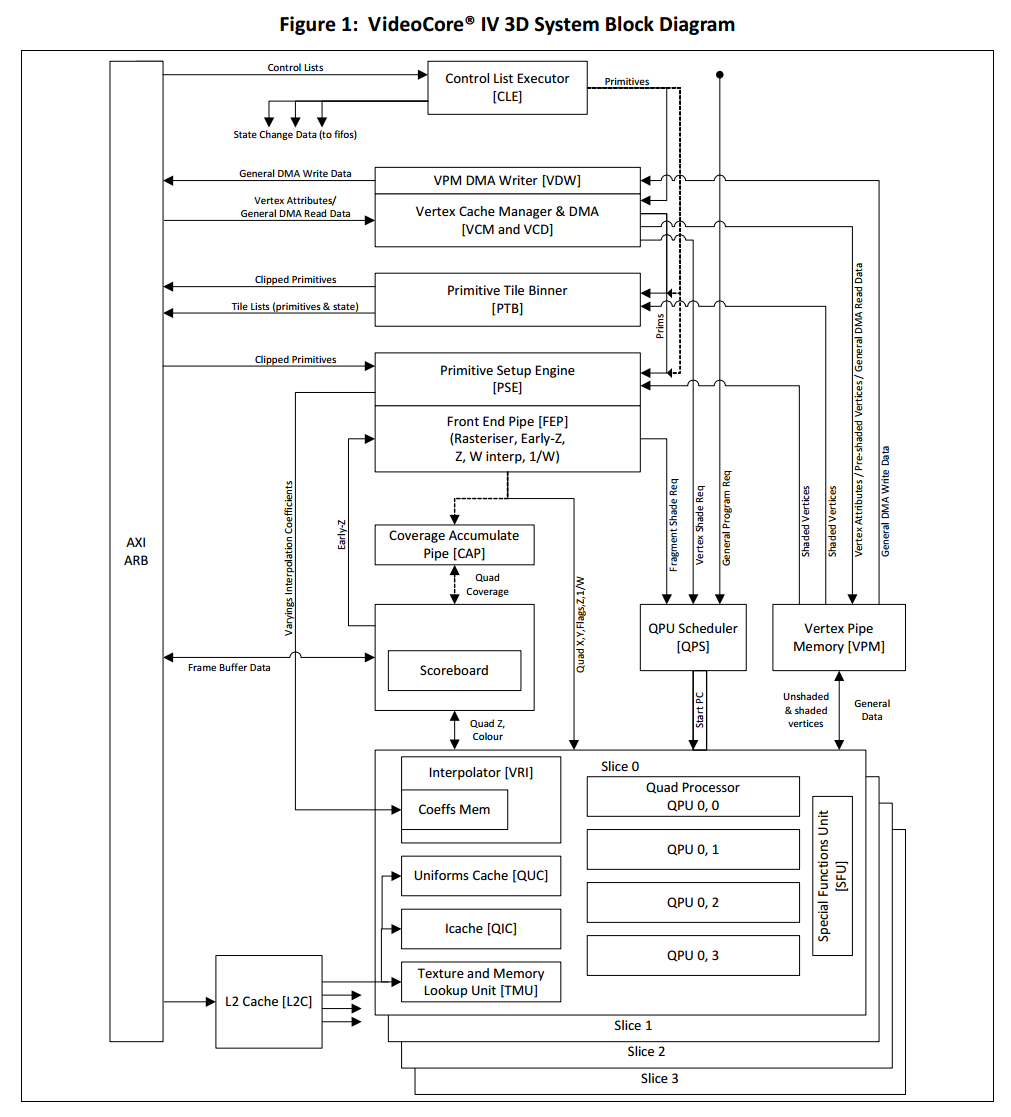
メモリ
下図はVideoCoreのアーキテクチャ図です。Uniform CacheかTexture and Memory Lookup Unit(TMU)かVertex Pipe Memory(VPM)を使ってHost-GPU間でデータをやり取りします。
VideoCore IV 3D Architecture Reference Guideより引用
UniformとTMUは読み込み専用です。これらはVPMよりloadが速そうです。ベンチマークはとっていないので具体的なパラメータはまだ分かりません。
Uniformは32bitのデータをシーケンシャルに読む為に使います。16個の成分全てに同じ値が読み込まれます。つまりスカラーのloadに適しています。TMUからは一回のloadで32bitのデータ16個を取り込むことができます。つまりベクトルのloadに適しています。(各スライス事に最大2つのTMU、TMU0とTMU1を置くことが出来ます。)
従いまして、以下の直積を計算するにはベクトル$\mathbf{a}$はTMU0でloadし、スカラー$b_i$はUniform Cacheでloadするようにするのが良いだろうという事になります。Row-majorですから$b_0,b_1,\ldots,b_{63}$は連続アドレスに配置されており、Uniform cacheで次々loadする事が出来ます。先ほど16x64にしたのはこのシーケンシャルなloadを出来るだけ長く取りたかったからです。
$$\mathbf{a}\mathbf{b}^T = (b_0\mathbf{a}, b_1\mathbf{a}, \ldots, b_{63}\mathbf{a})$$
最内ループの実装
ここまでの計算を実際にコードにしてみます。まず素朴に書くと以下のようになります。実数値以外の変数(A_curやA_baseなど)をどこに置くかは一旦考えません。
# 各列ベクトルを0で初期化
mov(ra0, 0.0)
mov(rb0, 0.0)
... # 省略
mov(rb31, 0.0)
iadd(A_cur, A_base, A_offs) # ベクトルaのアドレスを初期化
mov(B_cur, B_base) # ベクトルbのアドレスを初期化
mov(k, q) # ループインデックスを初期化
L.k_loop
mov(tmu0_s, A_cur) # ベクトルaの各成分のアドレスをセット
mov(uniforms_address, B_cur) # ベクトルbの先頭アドレスをセット
iadd(A_cur, A_cur, 4) # アドレスをインクリメント
iadd(B_cur, B_cur, B_stride) # アドレスをインクリメント
nop(sig='load tmu0') # TMU0からベクトルaをload(結果はレジスタr4に入る)
fmul(r0, r4, uniform) # uniformからb[0]をloadし、aと掛ける
fadd(ra0, ra0, r0) # 第0列に足しこむ
fmul(r0, r4, uniform) # uniformからb[1]をloadし、aと掛ける
fadd(rb0, rb0, r0) # 第1列に足しこむ
fmul(r0, r4, uniform) # uniformからb[2]をloadし、aと掛ける
fadd(ra1, ra1, r0) # 第2列に足しこむ
... # 省略
fmul(r0, r4, uniform) # uniformからb[62]をloadし、aと掛ける
fadd(ra31, ra31, r0) # 第62列に足しこむ
fmul(r0, r4, uniform) # uniformからb[63]をloadし、aと掛ける
fadd(rb31, rb31, r0) # 第63列に足しこむ
isub(k, k, 1) # インデックスを1減らす
jzc(L.k_loop) # 0じゃないならばループ最初に戻る(Jump if Z-flags are Clear)
nop() # delay slot
nop() # delay slot
nop() # delay slot
この時点ではloop bodyが138命令で、実質64命令分の数値計算をしているので64/138=46.4%の効率で演算器を使っています。様々なテクニックを使ってこれを最適化していきます。
まず、同時に実行できる加算と乗算を詰めていきます。
L.k_loop
mov(tmu0_s, A_cur) # ベクトルaの各成分のアドレスをセット
mov(uniforms_address, B_cur) # ベクトルbの先頭アドレスをセット
iadd(A_cur, A_cur, 4) # アドレスをインクリメント
iadd(B_cur, B_cur, B_stride) # アドレスをインクリメント
nop(sig='load tmu0') # TMU0からベクトルaをload(結果はレジスタr4に入る)
fmul(r0, r4, uniform)
fadd(ra0, ra0, r0).fmul(r0, r4, uniform)
fadd(rb0, rb0, r0).fmul(r0, r4, uniform)
fadd(ra1, ra1, r0).fmul(r0, r4, uniform)
... # 省略
fadd(rb30, rb30, r0).fmul(r0, r4, uniform)
fadd(ra31, ra31, r0).fmul(r0, r4, uniform)
fadd(rb31, rb31, r0)
isub(k, k, 1) # インデックスを1減らす
jzc(L.k_loop) # 0じゃないならばループ最初に戻る(Jump if Z-flags are Clear)
nop() # delay slot
nop() # delay slot
nop() # delay slot
条件分岐jzcの後の3命令はdelay slotといって、jzcを発行してから実際のジャンプが行われるまでに余分な3命令が必ず実行されます。ここでも演算を行う事が出来ます。
L.k_loop
mov(tmu0_s, A_cur) # ベクトルaの各成分のアドレスをセット
mov(uniforms_address, B_cur) # ベクトルbの先頭アドレスをセット
iadd(A_cur, A_cur, 4) # アドレスをインクリメント
iadd(B_cur, B_cur, B_stride) # アドレスをインクリメント
nop(sig='load tmu0') # TMU0からベクトルaをload(結果はレジスタr4に入る)
fmul(r0, r4, uniform)
fadd(ra0, ra0, r0).fmul(r0, r4, uniform)
fadd(rb0, rb0, r0).fmul(r0, r4, uniform)
fadd(ra1, ra1, r0).fmul(r0, r4, uniform)
... # 省略
fadd(ra30, ra30, r0).fmul(r0, r4, uniform)
isub(k, k, 1) # インデックスを1減らす
jzc(L.k_loop) # 0じゃないならばループ最初に戻る(Jump if Z-flags are Clear)
fadd(rb30, rb30, r0).fmul(r0, r4, uniform) # delay slotで実行
fadd(ra31, ra31, r0).fmul(r0, r4, uniform) # delay slotで実行
fadd(rb31, rb31, r0) # delay slotで実行
ここまででループ内部72命令中、64命令分を数値演算で埋める事が出来ましたので64/72=88.9%の効率で演算器を使えるようになりました。
アドレス計算のコードも最適化します。ここはいろいろと制約があり難しいです。まず、
uniforms_addressへの書き込み後2命令はuniformにアクセスしてはならない(リファレンスガイドP22)
というのがあります。また
-
tmu0_sをセット -
'load tmu0'シグナルを発行 -
r4をread
という順番を崩す事は出来ません。A_curの更新とtmu0_sへの書き込みは同時には行えません。シグナルの発行は他の演算のついでに発行する事が出来ます。これらの制約を守りつつパイプライン化して詰め込みます。
mov(uniforms_address, B_cur) # 最初の一回分はループに入る前にやる
mov(tmu0_s, A_cur)
iadd(A_cur, A_cur, 4)
nop(sig='load tmu0')
L.k_loop
mov(tmu0_s, A_cur)
iadd(B_cur, B_cur, B_stride)
iadd(A_cur, A_cur, 4).fmul(r0, r4, uniform)
fadd(ra0, ra0, r0).fmul(r0, r4, uniform)
fadd(rb0, rb0, r0).fmul(r0, r4, uniform)
fadd(ra1, ra1, r0).fmul(r0, r4, uniform)
... # 省略
fadd(ra30, ra30, r0).fmul(r0, r4, uniform)
isub(k, k, 1)
jzc(L.k_loop)
fadd(rb30, rb30, r0).fmul(r0, r4, uniform)
fadd(ra31, ra31, r0).fmul(r0, r4, uniform) # <- 最後のuniform,r4へのアクセス
fadd(rb31, rb31, r0, sig='load tmu0').mov(uniforms_address, B_cur) # <- 次のイテレーションを準備
ここで、ちょっとトリッキーな最適化を行ってisub(k, k, 1)を消します。変数kはループのインデックスですからスカラーです。それからB_curはuniforms cacheのベースアドレスでこれもスカラーです。従って、これらを一つのベクトル詰め込んでしまう事が出来ます。具体的には、ベクトル$\mathbf{b}$のアドレスをB_cur[0]に、kをB_cur[1]に入れ、B_stride[0]にストライド、B_stride[1]に-1を入れます。するとiadd(B_cur, B_cur, B_stride)でisub(k, k, 1)の計算もできます。
特定の成分へだけ代入を行うには、各成分に異なる2bit即値を代入出来るper-element load immediates命令でフラグをセットして、条件を満たす成分のみに計算結果を代入するconditional命令を使います。以下はB_stride[1]にだけ-1を代入する例です。
ldi(null, [1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1], set_flags=True)
mov(B_stride, -1, cond='zs') # move if Z-flag is Set
Uniform Cacheのベースアドレスに代入する部分では、第0成分の値が使われると決められている(リファレンスガイドP22)ので、特別な処理は不要です。
mov(uniforms_address, B_cur) # B_cur[0]がセットされる
jzcは16個の成分全てが0じゃないときにジャンプするという命令です。jzcがiadd(B_cur, B_cur, B_stride)でセットされたフラグを参照できるように、間の計算ではフラグをセットしない様にします。実際のコードは以下のようになります。
# B_cur, B_strideをセットアップする部分は省略
mov(uniforms_address, B_cur) # 最初の一回分はループに入る前にやる
mov(tmu0_s, A_cur)
iadd(A_cur, A_cur, 4)
nop(sig='load tmu0')
L.k_loop
mov(tmu0_s, A_cur)
iadd(B_cur, B_cur, B_stride)
iadd(A_cur, A_cur, 4, set_flags=False).fmul(r0, r4, uniform)
fadd(ra0, ra0, r0, set_flags=False).fmul(r0, r4, uniform)
fadd(rb0, rb0, r0, set_flags=False).fmul(r0, r4, uniform)
fadd(ra1, ra1, r0, set_flags=False).fmul(r0, r4, uniform)
... # 省略
fadd(ra30, ra30, r0, set_flags=False).fmul(r0, r4, uniform)
jzc(L.k_loop)
fadd(rb30, rb30, r0).fmul(r0, r4, uniform)
fadd(ra31, ra31, r0).fmul(r0, r4, uniform) # <- 最後のuniform,r4へのアクセス
fadd(rb31, rb31, r0, sig='load tmu0').mov(uniforms_address, B_cur) # <- 次のイテレーションを準備
ここまででループ内部が68命令まで削れましたので、演算器の使用効率は64/68=94.1%です。
最後に2命令使っている
mov(tmu0_s, A_cur)
iadd(B_cur, B_cur, B_stride)
を
iadd(B_cur, B_cur, B_stride).mov(tmu0_s, A_cur)
にしてもう一命令削りたいんですが、
uniforms_addressへの書き込み後2命令はuniformにアクセスしてはならない(リファレンスガイドP22)
に引っかかってしまいます。途中にjumpが入るので気にしなくても良いかもしれませんが、念のためこの問題を解決します。
L.k_loop
iadd(B_cur, B_cur, B_stride).mov(tmu0_s, A_cur)
iadd(A_cur, A_cur, 4, set_flags=False).fmul(r0, r4, uniform) # ここまでの間に2命令必要
fadd(ra0, ra0, r0, set_flags=False).fmul(r0, r4, uniform)
... # 省略
fadd(ra30, ra30, r0).fmul(r0, r4, uniform)
jzc(L.k_loop)
fadd(rb30, rb30, r0).fmul(r0, r4, uniform)
fadd(ra31, ra31, r0).fmul(r0, r4, uniform)
fadd(rb31, rb31, r0, sig='load tmu0').mov(uniforms_address, B_cur) # ここから
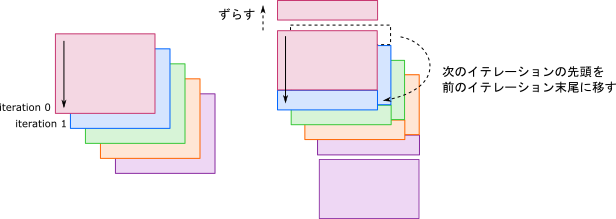
足りない1命令をjzcで補います。その為にソフトウェアパイプライニングをして、ループ全体を4命令ずらします。(リファレンスガイドでは記述が見つからなかったんですが、delay slot内でmov(tmu0_s, A_cur)を実行すると正しく動かなかった為、3命令ではなく4命令ずらしています。)
iadd(B_cur, B_cur, B_stride).mov(tmu0_s, A_cur)
iadd(A_cur, A_cur, 4, set_flags=False).fmul(r0, r4, uniform)
fadd(ra0, ra0, r0).fmul(r0, r4, uniform)
fadd(rb0, rb0, r0).fmul(r0, r4, uniform)
# ↑はみ出た分
L.k_loop
fadd(ra1, ra1, r0).fmul(r0, r4, uniform)
... # 省略
fadd(rb30, rb30, r0).fmul(r0, r4, uniform)
fadd(ra31, ra31, r0).fmul(r0, r4, uniform)
fadd(rb31, rb31, r0, sig='load tmu0').mov(uniforms_address, B_cur) # ここから
iadd(B_cur, B_cur, B_stride).mov(tmu0_s, A_cur)
jzc(L.k_loop) # <- こいつで1命令を補う
iadd(A_cur, A_cur, 4).fmul(r0, r4, uniform) # ここまでの間に2命令必要
fadd(ra0, ra0, r0).fmul(r0, r4, uniform)
fadd(rb0, rb0, r0).fmul(r0, r4, uniform)
# ↓はみ出た分(ここでループを抜ける)
fadd(ra1, ra1, r0).fmul(r0, r4, uniform)
... # 省略
fadd(ra31, ra31, r0).fmul(r0, r4, uniform)
fadd(rb31, rb31, r0)
何をやっているか分かりにくいと思うので絵を描いてみました。
この変換をすると少なくとも2イテレーション走ってしまうので$q\geq 2$である事を上で要請しています。
また、この変換によってiadd(B_cur, B_cur, B_stride)のタイミングが1イテレーション分ずれるのでkの初期値を1つずらす必要があります。
以上で最内ループは概ね完成です。途中を省略しないでLoop body書いてみると以下のような感じです。非常に高い密度で演算器を使えている事が分かると思います。
L.k_loop
fadd(ra1, ra1, r0).fmul(r0, r4, uniform)
fadd(rb1, rb1, r0).fmul(r0, r4, uniform)
fadd(ra2, ra2, r0).fmul(r0, r4, uniform)
fadd(rb2, rb2, r0).fmul(r0, r4, uniform)
fadd(ra3, ra3, r0).fmul(r0, r4, uniform)
fadd(rb3, rb3, r0).fmul(r0, r4, uniform)
fadd(ra4, ra4, r0).fmul(r0, r4, uniform)
fadd(rb4, rb4, r0).fmul(r0, r4, uniform)
fadd(ra5, ra5, r0).fmul(r0, r4, uniform)
fadd(rb5, rb5, r0).fmul(r0, r4, uniform)
fadd(ra6, ra6, r0).fmul(r0, r4, uniform)
fadd(rb6, rb6, r0).fmul(r0, r4, uniform)
fadd(ra7, ra7, r0).fmul(r0, r4, uniform)
fadd(rb7, rb7, r0).fmul(r0, r4, uniform)
fadd(ra8, ra8, r0).fmul(r0, r4, uniform)
fadd(rb8, rb8, r0).fmul(r0, r4, uniform)
fadd(ra9, ra9, r0).fmul(r0, r4, uniform)
fadd(rb9, rb9, r0).fmul(r0, r4, uniform)
fadd(ra10, ra10, r0).fmul(r0, r4, uniform)
fadd(rb10, rb10, r0).fmul(r0, r4, uniform)
fadd(ra11, ra11, r0).fmul(r0, r4, uniform)
fadd(rb11, rb11, r0).fmul(r0, r4, uniform)
fadd(ra12, ra12, r0).fmul(r0, r4, uniform)
fadd(rb12, rb12, r0).fmul(r0, r4, uniform)
fadd(ra13, ra13, r0).fmul(r0, r4, uniform)
fadd(rb13, rb13, r0).fmul(r0, r4, uniform)
fadd(ra14, ra14, r0).fmul(r0, r4, uniform)
fadd(rb14, rb14, r0).fmul(r0, r4, uniform)
fadd(ra15, ra15, r0).fmul(r0, r4, uniform)
fadd(rb15, rb15, r0).fmul(r0, r4, uniform)
fadd(ra16, ra16, r0).fmul(r0, r4, uniform)
fadd(rb16, rb16, r0).fmul(r0, r4, uniform)
fadd(ra17, ra17, r0).fmul(r0, r4, uniform)
fadd(rb17, rb17, r0).fmul(r0, r4, uniform)
fadd(ra18, ra18, r0).fmul(r0, r4, uniform)
fadd(rb18, rb18, r0).fmul(r0, r4, uniform)
fadd(ra19, ra19, r0).fmul(r0, r4, uniform)
fadd(rb19, rb19, r0).fmul(r0, r4, uniform)
fadd(ra20, ra20, r0).fmul(r0, r4, uniform)
fadd(rb20, rb20, r0).fmul(r0, r4, uniform)
fadd(ra21, ra21, r0).fmul(r0, r4, uniform)
fadd(rb21, rb21, r0).fmul(r0, r4, uniform)
fadd(ra22, ra22, r0).fmul(r0, r4, uniform)
fadd(rb22, rb22, r0).fmul(r0, r4, uniform)
fadd(ra23, ra23, r0).fmul(r0, r4, uniform)
fadd(rb23, rb23, r0).fmul(r0, r4, uniform)
fadd(ra24, ra24, r0).fmul(r0, r4, uniform)
fadd(rb24, rb24, r0).fmul(r0, r4, uniform)
fadd(ra25, ra25, r0).fmul(r0, r4, uniform)
fadd(rb25, rb25, r0).fmul(r0, r4, uniform)
fadd(ra26, ra26, r0).fmul(r0, r4, uniform)
fadd(rb26, rb26, r0).fmul(r0, r4, uniform)
fadd(ra27, ra27, r0).fmul(r0, r4, uniform)
fadd(rb27, rb27, r0).fmul(r0, r4, uniform)
fadd(ra28, ra28, r0).fmul(r0, r4, uniform)
fadd(rb28, rb28, r0).fmul(r0, r4, uniform)
fadd(ra29, ra29, r0).fmul(r0, r4, uniform)
fadd(rb29, rb29, r0).fmul(r0, r4, uniform)
fadd(ra30, ra30, r0).fmul(r0, r4, uniform)
fadd(rb30, rb30, r0).fmul(r0, r4, uniform)
fadd(ra31, ra31, r0).fmul(r0, r4, uniform)
fadd(rb31, rb31, r0, sig='load tmu0').mov(uniforms_address, r2)
iadd(r2, r2, r3).mov(tmu0_s, r1)
jzc(L.k_loop)
iadd(r1, r1, 4).fmul(r0, r4, uniform) # delay slot
fadd(ra0, ra0, r0).fmul(r0, r4, uniform) # delay slot
fadd(rb0, rb0, r0).fmul(r0, r4, uniform) # delay slot
まとめると16x64の部分行列をSIMDで計算するコードを、67命令中の64命令(95.5%)が実数値演算、レジスタファイルの100%が実数値用という高い効率で書くことが出来ました。Uniform Cacheが十分に速ければ良い性能が出るんではないかと思います。
行列成分以外をどこに置くか?
レジスタファイルを使い切ったので、その他の変数をどこに置くのかという問題がまだ残っていますが大丈夫です。最内ループではアキュムレータr0,r1,r2,r3のうちr1,r2,r3が未使用ですから
-
A_curをr1に -
B_curをr2に -
B_strideをr3に
割り当てる事が出来ます。先ほどのisub(k, k, 1)の削除はこの為にも必要でした。
また、A_curは16成分を使い切っていますが、B_curとB_strideはまだ2成分しか使っていません。空いている28ワードに行列のアドレスとかサイズとかそういった値を置くことが出来ます。今回は以下のように配置しました。$\alpha$と$\beta$はアドレスcoef_addrに置きました。Uniforms Cacheを使って読むことが出来ます。
k-loopではiadd(r2, r2, r3)のZフラグをチェックするので、第1成分以外が0になることのない様に注意します。(先日は誤って$\alpha$と$\beta$を直に置いてしまい、$\alpha=0.0$もしくは$\beta=0.0$の時にk-loopが正しく回らないというバグを埋め込んでしまいました。)
レジスタファイルBのアドレス37(私のライブラリではbroadcastという名前)に値を書き込むと成分0の値が16成分すべてにbroadcastされます(リファレンスガイドP38)。これと成分を回転させるvector rotation命令を使うと特定の成分だけを1命令(しかも乗算器のみ)で取り出す事が出来ますので、この格納方法によるペナルティは小さいです。
例えば、r2の5番目の成分を取り出したければ以下のようにします。
... # 一つ前の命令ではr2にアクセスしてはいけない
rotate(broadcast, r2, -5)
mov(r0, r5) # 結果は特殊アキュムレータr5に入る。
vector rotationはイレギュラーな順番でパイプラインにアクセスしますから、他の命令と異なりrotateの前に待ち時間が必要です。
ベクトルレジスタに詰め込む以外だと
- 上でやったようにUniforms CacheのBase Addressだけ記憶しておき、必要になった時にuniformから読む。
- プログラムを実行前に書き換えて、命令の即値部分に埋め込んでしまう。
- 計算して作れるものはそうする。
などの工夫が出来ます。たまにしか使用しない値の為にレジスタを使うのはもったいないので、こういった努力をしましょう。
行列Cへの足しこみ
$\alpha AB + \beta C$ の$AB$の部分の計算が出来るようになったので、次は$\alpha(\cdots)+\beta C$の部分の計算です。Hostに書き戻す必要があるのでVPMに置くことにします。(TMUでloadし、VPMに書き込むという手もありそうです。どっちが良いかはまだ分かりません。)
VPMのサイズは64x16です。、上で計算したものがちょうど収まります。
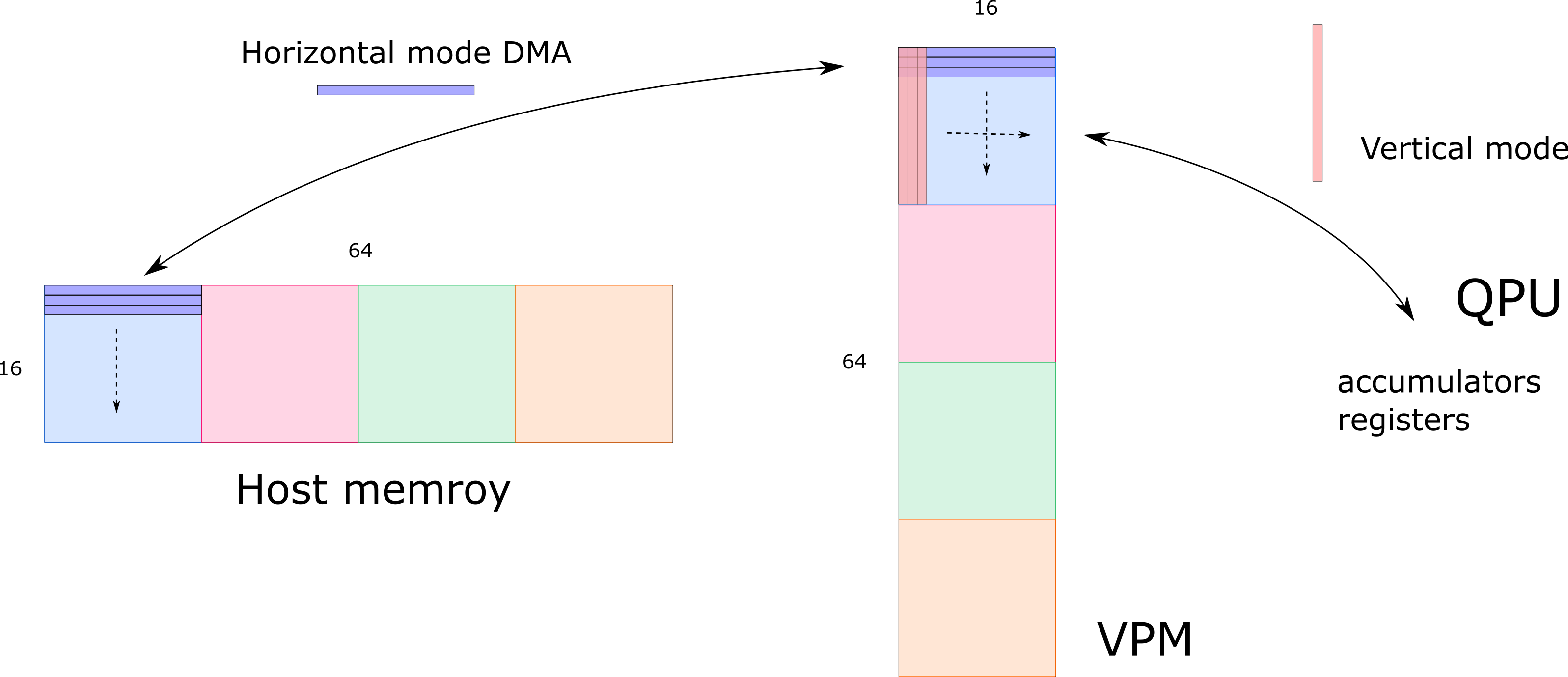
Host memory、VPM間はDMAで転送します。一度に16本のベクトルを転送できるので16x16のブロックに分けて4回転送します。
行列はHost memoryにはRow-majorで格納されていますから、Horizontal modeで転送した方が、多分速いんじゃないかと思います。ホントかどうかは知りません。一方、QPUでは列ベクトル単位でデータを持っていますから、VPM, QPU間はVertical modeでやり取りします。
DMAはかなり時間が掛かるはずなので、待ち時間を無駄にしないように1つめのブロックの転送は先ほどソフトウェアパイプライニングをしてはみ出した所と重ねます。63命令(=252クロック)分の待ち時間を有効に使えます。
# 行列Cのload用ストライドをセット。これは定数なのでプログラムの一番最初に一回だけやればよい。
rotate(broadcast, r2, -C_STRIDE_IDX)
setup_dma_load_stride(r5, tmp_reg=r1)
# 行列Cのstore用ストライドをセット。これもプログラムの一番最初に一回やればよい。
ldi(r1, 4*16)
isub(r1, r5, r1) # この引き算が必要な理由はリファレンスガイドのTable35を参照。
setup_dma_store_stride(r1)
... 省略
# (先ほどのループ(k-loop)を抜けた所。)
# 最初のブロックのloadを発行
setup_dma_load(mode='32bit horizontal', Y=0, nrows=16, mpitch=0)
rotate(broadcast, r2, -C_BASE_IDX)
start_dma_load(r5).mov(r3, r5) # Cのベースアドレスを覚えておく。
# ↓ ソフトウェアパイプライニングによってk-loopからはみ出した計算で、通信を出来るだけ隠蔽する。
fadd(ra1, ra1, r0).fmul(r0, r4, uniform)
fadd(rb1, rb1, r0).fmul(r0, r4, uniform)
... # 省略
fadd(ra31, ra31, r0).fmul(r0, r4, uniform)
fadd(rb31, rb31, r0)
wait_dma_load() # ここでDMAの完了を待つ。
転送時間を隠蔽するにはもう一つ方法があります。各QPUは2つのハードウェアスレッドを走らせる事が出来るので、交互に上手く切り替えれば通信を隠蔽して演算器をフル稼働させる事が出来ます。
いろいろなパラメータがまだ不明な状態でやっているので、どうするのがベストかは実験してみなければ分かりません。ただ、スレッド化すると各スレッドが使えるレジスタは半分に減り、最内ループの効率が少し下がります。スレッド切り替えのオーバーヘッドもありますから、シングルスレッドで上手くやれるならばその方が良いはずです。
1ブロックをloadしたら、次のブロックのloadを先に発行してから$\alpha(\cdots)+\beta C$の計算を行います。掛け算が2回で足し算が1回ですから、加算器が1回分余ります。この隙間に次のイテレーションの為に列ベクトルを0初期化する処理を突っ込みます。
# alpha, betaを読む為にuniforms cacheを設定
rotate(r0, r2, -COEF_ADDR_IDX)
mov(uniforms_address, r0)
# 2つめのブロックのロードを発行
setup_dma_load(mode='32bit horizontal', Y=16, X=0, nrows=16, mpitch=0)
ldi(r0, 4*16)
iadd(vpm_ld_addr, r3, r0)
# 1つめのブロックに対するVPMアクセスをセットアップ
setup_vpm_read(mode='32bit vertical', Y=0, X=0, nrows=16)
setup_vpm_write(mode='32bit vertical', Y=0, X=0)
# alpha, betaを取り出す。
mov(r1, uniform) # r1=alpha
mov(broadcast, uniform) # r5=beta
# 1つめのブロックの足しこみ
fmul(ra0, ra0, r1) # ABの一列にalphaを掛ける。
fmul(r0, vpm, r5) # Cの一列にbetaを掛ける。
fadd(vpm, ra0, r0).fmul(rb0, rb0, r1) # 左: 足してvpmに書き戻す。 右: 次の列の計算
mov(ra0, 0.0) .fmul(r0, vpm, r5) # 左: 次のイテレーションの為にra0を初期化。 右: 次の列の計算
... # 省略
こんな感じで計算と転送を交互に詰め込みます。
以上で、16x64の部分行列の計算が完了しました。
次回に続く。
すごく長くなってしまったので、Advent Calendarをもう一日使わせてもらって続きを書きます。
次は
- 外側のi-ループ,j-ループを書きます。
- 12個のQPUを使って並列実行します。
- この際の同期処理について説明します。
- ベンチマークを取ります。速くなっていると良いな~。