はじめに
部活で後輩にPythonを教えることになり、円周率を求めたのでその内容を残しておきます。
モンテカルロ法とは
モンテカルロ法 (モンテカルロほう、英: Monte Carlo method, MC) とはシミュレーションや数値計算を乱数を用いて行う手法の総称。 元々は、中性子が物質中を動き回る様子を探るためにスタニスワフ・ウラムが考案しジョン・フォン・ノイマンにより命名された手法。(モンテカルロ法より引用)
というわけで、大雑把に言えば乱数を使って何かを求めることです。
モンテカルロ法で円周率を求める方法
今回はモンテカルロ法で、つまり乱数を使って円周率を求めます。具体的な方法を説明します。
(1)正方形と円の面積
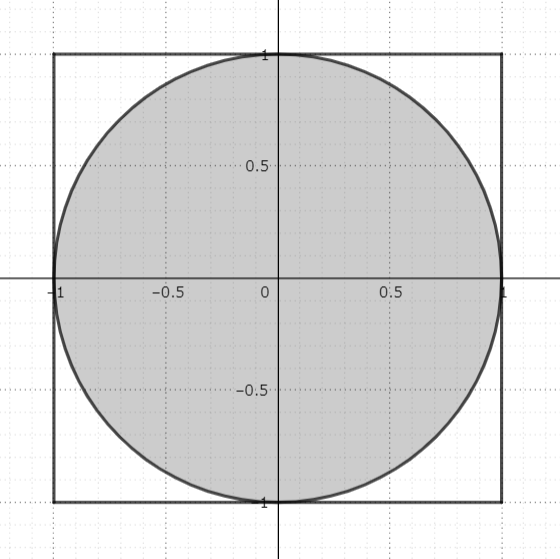
原点を中心とした半径1の円と、それに外接する2×2の正方形があります。モンテカルロ法で円周率を求めるには、これらの面積の比に着目します。
まずは、円の面積を考えます。円の面積は皆さんご存知の通り半径×半径×πです。この円の場合半径は1なので、円の面積=πということになります。同様に四角形の面積を求めます。この四角形は2×2の正方形なので、四角形の面積=4になります。
(2)たくさん点を打つ
先ほど、モンテカルロ法とは乱数を使って何かを求めること、という説明をしました。乱数はここで使います。見出しにもある通り、今回は先ほどの図の四角形の中にランダムなたくさんの点を打ち、これを計算に使います。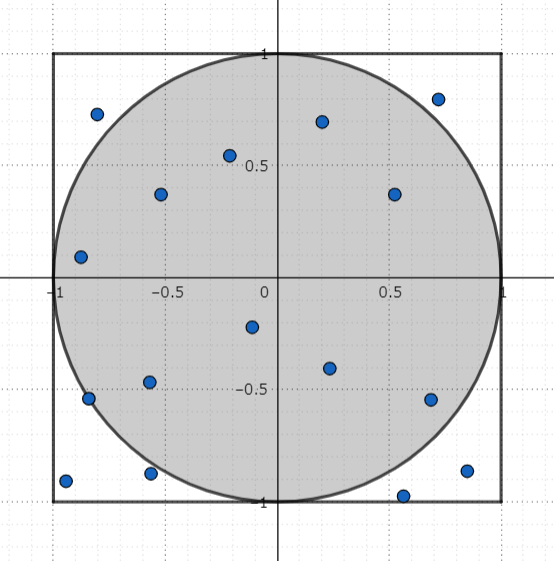
(3)面積と点の数の関係
ある図形に同じ密度でランダムな点を打った時、面積は点の数と比例しています。簡単に言うと、面積が二倍になれば点の数も二倍になるということです。これが今回作るプログラムで一番重要な点です。
円周率を求めるには
これらの情報を使って,どのように円周率を求めるのかを説明します。
まず初めに、(1)を使います。(1)では四角形の面積と円の面積を求めました。この二つから円周率を求めることを考えると、
式1)
円の面積÷四角形の面積×4
=π÷4×4
=π
という計算により円周率を求められることが分かります。さて、(2)では、点をたくさん打って円周率を求めること、(3)では面積は点の数と比例しているということを説明しました。円周率を求める場合は、たくさん点を打ち、その点が円の中に入っている数と円の面積が、四角形の中に入っている数と四角形の面積が、それぞれ対応しています。言葉でもよく意味が分からないので、式で表すと、
式2)
・円の面積 ≒ 円内の点の数 × k
・四角形の面積 ≒ 四角形内の点の数 × k
(kは比例定数)
と表すことができます。kについてですが、例えば円内の点の数が6個、四角形内の点の数が8個だったとします。この時、「面積=点の数」としてしまうとこれは正しくありません。実際には円の面積は約3、四角形の面積は4だからです。両者とも点の数が面積の2倍になってしまっています。このずれを修正するためには両者の点の数に1/2を掛けた値を面積とすればよいですね。kはこの時の1/2と同じ役割をしています。ここで、式1と式2を組み合わせると、
式3)
円の面積÷四角形の面積×4
≒(円内の点の数×k) ÷ (四角形内の点の数×k) × 4
=円内の点の数 ÷ 四角形内の点の数 × 4
≒π
となります(kは約分されて消えます)。この式の真ん中の、(円内の点の数) ÷ (四角形内の点の数) × 4 ≒ πをプログラム内で使用します。
実際にプログラムを書く
ここからはいよいよpythonを使ってプログラムを書いていきます。
環境の準備
「pythonでプログラミングする環境がパソコンに入っていない」という状況だったので、ブラウザ上でpythonをプログラミングすることのできるサイトを使用しました。こちらのリンクを開いてください。
ブラウザでプログラミング・実行ができる「オンライン実行環境」| paiza.IO
このリンクを開くと、次のような画面が表示されると思います。つぎにpythonでプログラミングするために、左上のPHPと書かれたところを押して、Python3に切り替えてください。

これで準備が整いました。いよいよプログラミングを始めていきます。
円内の点の数、四角形内の点の数。
先ほど、円内の点の数と四角形内の点の数を使って円周率を求めると説明しました。なので、これらの数値を保存しておく変数を用意します。プログラミングにおける変数とは、数字や文字列を入れるための箱のような存在です。サイトの黒い画面に次のように書き足してください。
# coding: utf-8
# Your code here!
square = 0
circle = 0
今書いた、squareには四角形内の点の数が、circleには円内の点の数が入る変数(=箱)です。変数はこのようにして準備します。まだ点を一つも打っていないのでどちらも0にしておきます。
繰り返し処理
モンテカルロ法で円周率を求めるにはたくさんの点を打ちます。そのため点を打つ処理を繰り返すためのプログラムを書く必要があります。今回は繰り返しには、for n in range(繰り返し回数):を使います(ほかにも方法はありますが、今回はこれを使います)。先ほどのプログラムに次のコードを書き加えてください。
# coding: utf-8
# Your code here!
square = 0
circle = 0
for i in range(100):
print("abc")
これを実行すると、abcと100回表示されます(print("abc")は、abcという文字列を表示するための命令です)。つまり、print("abc")を100回繰り返した、ということになります。これが繰り返し処理です。pythonで繰り返し処理を行う際の注意点は、繰り返す部分は左側に空白(インデント)を入れる必要があるということです。試しに次のようにプログラムを書き換えてみてください。
# coding: utf-8
# Your code here!
square = 0
circle = 0
for i in range(100):
print("hello")
print("good bye")
これを実行すると、100回のprint("hello")の後にprint("good bye")が一度だけ実行されているということが分かります。これはprint("good bye")が繰り返しから除外されていることを意味します。このため、繰り返す部分は左側に空白を入れる必要があります。この空白はTabキーを押すことで入力できます(普通のスペースでも構いません)
四角形の中にランダムに点を打つ。
今度はランダムに点を打っていきます。ランダムに点を打つといっても、プログラム内で実際に点を打つことはできません。そのため、点を打つ代わりに、点の座標を決めるということを行います。点を打つ場所は四角形の中なので、その座標の範囲は-1<x<1,-1<y<1になります(冒頭の図参照)。この範囲でランダムな座標を決めれば、ランダムな点を打ったことと同じことになります。次のようにコードを書き換えてください。
# coding: utf-8
# Your code here!
import random
square = 0
circle = 0
for i in range(100):
x = random.uniform(-1,1)
y = random.uniform(-1,1)
print(x)
print(y)
たくさんのランダムな数字が表示されれば成功です。このコードの一つ目の重要な点は、冒頭のimport randomです。これによりランダムな数字を使えるようになります。二つ目にrandom.uniform(-1,1)です。random.unifrom(a,b)は、aからbまでのランダムな小数を表します。今回はx,yの範囲通りに-1から1までと設定します。 これでランダムに打った点の座標を決定することができました。
四角形の中に打った点を記録する
先ほどランダムな点の座標を決定しました。四角形の範囲内に打った点は必ず四角形の中にあります(当たり前ですね)。つまり四角形内の点の数が一つ増えたということになります。なので、四角形内の点の数を表すsquareを一つ増やす必要があります。次のようにコードを書き換えてください。
# coding: utf-8
# Your code here!
import random
square = 0
circle = 0
for i in range(100):
x = random.uniform(-1,1)
y = random.uniform(-1,1)
square += 1
print(square)
これを実行すると1,2,3,...,100という数字が表示されると思います。表示されている数字は、print(square)で表示されたsquareなので、点を打つごとに一つずつ増えていることが分かると思います(文字列の表示には"hello"のように"で囲む必要がありますが、今回表示させているものは変数なので囲む必要はありません)。
円の中の点の数を記録する
四角形の場合、打った点のすべてが四角形に入っていたので簡単なのですが、円の場合は範囲内なのかそうでないのかを判断する必要があります。これには原点からの距離を考えます。次の図を見てください。
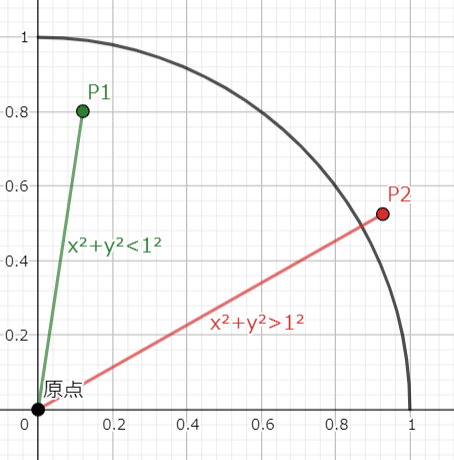
今回の円の半径は1です。また、三平方の定理から、打った点と原点との距離の二乗はx²+y²であることが分かります。この点が円の中にあるということは、中心からの距離が1以下であるということです。つまり、x²+y²<1²の時、この点は円内にあります。この条件を満たすときに円内の点の数を一つ増やせばよさそうですね。次のようにコードを書き換えてください。
# coding: utf-8
# Your code here!
import random
square = 0
circle = 0
for i in range(100):
x = random.uniform(-1,1)
y = random.uniform(-1,1)
square += 1
if x**2 + y**2 < 1**2:
circle += 1
print(circle)
これを実行すると、四角形の時とは違って、1,2,2,3,4,4,...のように数字が増えるときと増えないときがあります。数字が増えたときは、打った点が円内だったということです。このコードの重要な点は二つあります。一つ目はif文です。これは英語のもし~なら~と全く同じ意味で使えます。今回の場合は、もしx²+y²<1²ならcircleを1増やすという意味です。これも繰り返しの時と同様、左側にスペースを空ける必要があります。二つ目は2乗というものをどのように表記するのか、ということです。pythonで累乗を表すには**を使います。今回はxの2乗なので、x**2となります。
いよいよ円周率を求める
ここまで来れば後は円周率を求めるだけです。これには前に説明した**(円内の点の数) ÷ (四角形内の点の数) × 4 ≒ π**を使います。次のようにコードを書き換えてください。
# coding: utf-8
# Your code here!
import random
square = 0
circle = 0
for i in range(100):
x = random.uniform(-1,1)
y = random.uniform(-1,1)
square += 1
if x**2 + y**2 < 1**2:
circle += 1
print(circle / square * 4)
/は割り算、*は掛け算を表しています。これを実行するとだいたい3くらいの値になると思います。確かに円周率に近づいていますが、精度が良くないかもしれません。このような時は、繰り返しの回数を増やすことで精度を高めることができます。for i in range(100):を、for i in range(10000):に書き換えて実行してください。そうすればより円周率に近い値を求めることができると思います。