アブスト
MATLABでライフゲームを実装し,アニメーションを表示します.
MATLABでライフゲーム~!可視化が楽! pic.twitter.com/EtdS4xjCEo
— 9W3R7Y@Mix依頼⭕️ (@qwerty_16180339) January 31, 2021
Conway's Game of Lifeって何?
既にご存じの方も多いと思いますが,とりあえずWikipediaの説明を見てみます.(今回の記事,参考文献が全部wikipediaですが許してください)
ライフゲーム (Conway's Game of Life[1]) は1970年にイギリスの数学者ジョン・ホートン・コンウェイ (John Horton Conway) が考案した生命の誕生、進化、淘汰などのプロセスを簡易的なモデルで再現したシミュレーションゲームである。単純なルールでその模様の変化を楽しめるため、パズルの要素を持っている。生物集団においては、過疎でも過密でも個体の生存に適さないという個体群生態学的な側面を背景に持つ。セル・オートマトンのもっともよく知られた例でもある。
ざっくりいうと,__簡単なモデルで,生命のふるまいをシミュレーションするゲーム__です.
実際どんな生き物が生成されるのかというと,例えばこんなやつ(Wikipediaより引用).
あとこんなやつも(Wikipediaより引用).
めっちゃ可愛い!!!!!!!
一生眺めてられる!!!!!!!!!!
という訳で,ルールの説明に移ります.
ルール
ルールはめちゃくちゃシンプルで,以下の通りです(Wikipediaより引用).
ライフゲームでは初期状態のみでその後の状態が決定される。碁盤のような格子があり、一つの格子はセル(細胞)と呼ばれる。各セルには8つの近傍のセルがある (ムーア近傍) 。各セルには「生」と「死」の2つの状態があり、あるセルの次のステップ(世代)の状態は周囲の8つのセルの今の世代における状態により決定される。
セルの生死は次のルールに従う。
誕生:死んでいるセルに隣接する生きたセルがちょうど3つあれば、次の世代が誕生する。
生存:生きているセルに隣接する生きたセルが2つか3つならば、次の世代でも生存する。
過疎:生きているセルに隣接する生きたセルが1つ以下ならば、過疎により死滅する。
過密:生きているセルに隣接する生きたセルが4つ以上ならば、過密により死滅する。
ざっくりまとめると,グリット状のマス目の一つ一つにセルが存在し,各セルは近傍の生きたセルの個数に応じて新たな状態に遷移する,これだけです.シンプル.
では実装に移りましょう.
実装
まず,__セルの生死は0と1で表す__ことにします.何かと便利なので.また,グリッド状の__盤面は行列として扱う__ことにします.
次に,盤面の初期化について考えます.手動で各セルの値を設定するのは面倒なので,適当な割合で0と1をランダムに配置することにしましょう.
ここからはライフゲームのルールの実装ですね.すべてのセルに対して次の状態を求める必要があるので,盤面の大きさに応じた,(1) x方向・(2) y方向へのループ__が必要になります.また,近傍のセルも調べる必要があるので,さらに(3) x方向・(4) y方向の3回のループ__が必要になります.(計算量のことはとりあえず無視します)
簡単な図を書くと,こんな感じになります.黄色のセルは,赤いセルの近傍のセルです.図は,赤いセルから黒の斜線のセルの状態を調べるときのループのイメージです.
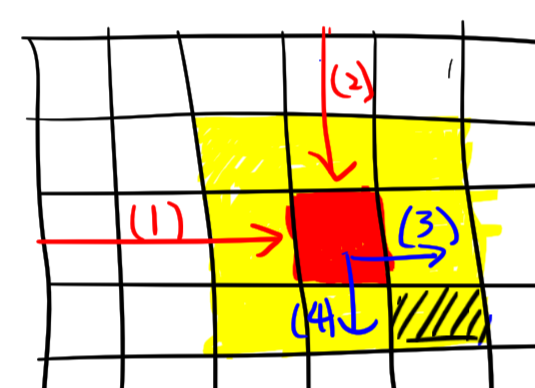
ここで問題点が二つあります.一つ目は,__近傍を調べるループで,そのセル自身も調べてしまうということです.__3×3のループをするわけですから,当然,中央のそのセル自身も調べてしまうことになります.二つ目は,__処理対象のセルが盤面の縁に存在するとき,近傍のセルの一部が盤面の外に飛び出してしまうということです.__このことを忘れるとindex out of boundsになります.
これらの問題点は簡単に解決できます.__if文で,自分自身やエラーとなるアクセスを除外__すればよいだけです.
近傍の生きたセルの数を数えるためのループが出来上がったら,実際に次のセルの状態を決定する処理を書きましょう.まずは近傍の生きたセル数をカウントする変数sumを0に初期化します.次に__(3)(4)のループの中で,近傍の各セルの値をsumに加算します.__死んだセルを0,生きたセルを1と表現しているのですから,セルの値の合計は生きたセルの個数となります.
生きたセルがカウント出来たら,ルールを基にセルの値を決定すればよいだけですね.ルールをもう一度確認しましょう.
セルの生死は次のルールに従う。
誕生:死んでいるセルに隣接する生きたセルがちょうど3つあれば、次の世代が誕生する。
生存:生きているセルに隣接する生きたセルが2つか3つならば、次の世代でも生存する。
過疎:生きているセルに隣接する生きたセルが1つ以下ならば、過疎により死滅する。
過密:生きているセルに隣接する生きたセルが4つ以上ならば、過密により死滅する。
ルールを読むと,まず当該のセルが生きているのか死んでいるのかを判別し,その後近傍の生きたセルの個数に応じて次の値を決定するのが楽そうです.
ここで注意すべきことは,__値を決定した後,すぐに値を更新してはいけない__ということです.あるセルの次の値が決定したとしても,まばほかのセルの次の値は決定していないので,それらのセルの次の値の決定を待つ必要があります.そのため,__盤面保存用の行列の他に,次のセルの値を保管しておく配列を作成し,ひとまずそこにデータを溜める__ことにしましょう.すべてのセルの次の値が決定してから,盤面の値を更新しましょう.
以上でライフゲームのルールの実装は終わりです.あとは,__任意の回数だけ,このルールに基づいたセルの状態の更新を繰り返す__ことになります.無限に見たかったらwhile Trueでもよいかもしれませんが,__時間を忘れる可能性があり危険__ですので,1000回に制限しておきましょう.
最後にこれを可視化すればよさそうです.行列の可視化にはspy()が便利です.また,リアルタイムにプロットを表示する場合には,プロットの直後にdrawnowと記述すればOKです.フレームレートを制限したいので,プロットするたびに1/24秒pauseすることにします.
以上が実装方法の説明となります.
ソースコード
size = 100; %盤面の大きさ
map = rand(size); %盤面を格納する配列
next = zeros(size); %次の盤面を格納する配列
init_rate = 0.3; %初期化時に生きたセルが生成される確率
t = 0; %時刻
TIME_END = 1000; %シミュレーションの上限
%盤面の初期化
for x = 1:size
for y = 1:size
if map(x,y) < init_rate
map(x,y) = 1;
else
map(x,y) = 0;
end
end
end
while t < TIME_END
%盤面の可視化
spy(map);
drawnow;
pause(1/24);
%次の盤面を取得
for x = 1:size
for y = 1:size
%近傍の生きたセル数を初期化
sum = 0;
%近傍のセルを調べる
for i = -1:1
for j = -1:1
if (i~=0 || j~=0) && ... %自分自身でない
0 <x+i && x+i <= size && ...%x座標が範囲内
0 <y+j && y+j <= size %y座標が範囲内
%セルの値をsumに追加し,生きたセルをカウント
sum = sum + map(x+i,y+j);
end
end
end
%近傍の生きたセル数から次の状態を計算し,nextに格納
if map(x,y) == 0
%誕生
if sum == 3
next(x,y) = 1;
%誕生しない
else
next(x,y) = 0;
end
else
%過疎・過密
if sum <= 1 || 4 <= sum
next(x,y) = 0;
%生存
else
next(x,y) = 1;
end
end
end
end
%mapを更新
map = next;
%時間を進める
t = t + 1;
end
完成形はこんな感じ.なんか動いてて可愛いですね.
MATLABでライフゲーム~!可視化が楽! pic.twitter.com/EtdS4xjCEo
— 9W3R7Y@Mix依頼⭕️ (@qwerty_16180339) January 31, 2021
おわりに
お読みいただきありがとうございました!ライフゲームは眺めてるだけで時間が過ぎていくので,気を付けましょう!(自戒)