ルービックキューブを解くプログラムを書いてみよう(前編:キューブを操る実装)

はじめに

この記事はルービックキューブ Advent Calendar 2018 の14日目の記事です。
昨日の記事は望月さんの「ラノベで覚えよう！目隠しキューブ。「恋するイヤーマフ」」でした。

本連載では、ルービックキューブを解くプログラムをPythonで実装しながら、その仕組みを勉強します。
ルービックキューブを解くプログラムと言っても、どれくらい頑張って高速化・効率化するかなどあると思うので、今回の記事では、大体1秒位 & 20手強くらいで解くプログラムを書くのを目標に、コードのわかりやすさ重視でやっていきましょう。

ルービックキューブを効率よく解くアルゴリズムとしてTwo-Phase-Algorithmというものが広く使われています。
本連載でも、Two-Phase-Algorithmを実装します。

まだ、前編しか書けていないので、内容は変わるかもしれませんが、

• 前編と中編では、実装する前に必要となる前提知識
  • 前編: ルービックキューブの状態と操作をプログラムで表す方法について
  • 中編: ルービックキューブの探索について
• 後編でTwo-Phase-Algorithmの実装

という構成を想定しています。
連載形式になった理由はただ担当日に間に合わなかっただけです。
中編と後編は来年のアドベントカレンダーで書きます。

追記: 中編を書きました ルービックキューブを解くプログラムを書いてみよう(中編) (IDA*探索) - Qiita
追記: 後編を書きました ルービックキューブを解くプログラムを書いてみよう(後編:状態のindex化, Two-Phase-Algorithm)

ルービックキューブを解くプログラムを使いたいだけの場合

この記事は、ルービックキューブを解くプログラムの仕組みを勉強しようという趣旨のものですので、ルービックキューブを解くプログラムを利用したいだけの場合は、自分で書くのではなく、既存のツールを使うのが良いでしょう。

自分の知る範囲では、

• Java: 公式大会のスクランブルプログラムとしても採用されている https://github.com/cs0x7f/min2phase
• Python: Two-Phase-Algorithmを考案したKociemba氏本人による https://github.com/hkociemba/RubiksCube-TwophaseSolver や https://github.com/muodov/kociemba
• JavaScript: https://github.com/cs0x7f/min2phase.js
• C: https://github.com/kotarot/chample

などがあります。

環境

今回の実装は、Python3.6以上の環境で行います。

以下で出てくるコードをColaboratoryノートブック化したもの
も用意したので、[Play Groundで開く] クリックし、順に実行しながら進めれば、環境構築など不要で楽だと思います。

ルービックキューブの前提知識

ルービックキューブの回転記号

記事中では、ルービックキューブの回転を表すのに回転記号を使います。
3x3x3 回転記号 | tribox を参考に理解しておいてください。

記事中では、次のような配色のルービックキューブを使い、

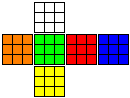
常に、上面 (U面)が 白、手前面 (F面) が緑で持った状態で説明し、2層回しや持ち替えは扱いません。

ルービックキューブのパーツ

ルービックキューブには、センターパーツ、コーナーパーツ、エッジパーツがあります。

センターパーツ

センターパーツは、各面の中心の1色パーツで、6個あります。
センターパーツは、各面を回しても動きません。
白上緑手前でずっと回していくことを考えるので、センターパーツは無視します。

コーナーパーツ

コーナーパーツは、立方体の角にあたる部分にある3色パーツで、8個あります。
コーナーパーツは、各面を回すと動きます。
コーナーパーツは、同じ場所にねじれて収まることもできるので、コーナーの状態を表す情報としては、どのパーツがどの位置にあるかということの他に、パーツが3通りのうちどちらを向いているかという情報も必要です。

エッジパーツ

エッジパーツは、立方体の辺にあたる部分にある2色パーツで、12個あります。
エッジパーツも、各面を回すと動きます。
エッジも、同じ場所に反転して収まることもできるので、エッジの状態を表す情報としては、どのパーツがどの位置にあるかということの他に、パーツが2通りのうちどちらを向いているかという情報も必要です。

ルービックキューブの操作の数え方

これから、なるべく短い操作で揃えるプログラムを書くことを目指すことになるので、操作の数え方を決めておきます。

本連載では、同じ面を回す限り、90度回転も180度回転も "1手" とみなします。
そのため、R2 は R + Rの2手カウントではなく、1手で数えます。

これをHalf Turn Metricと言います。

ルービックキューブのパーツのナンバリング

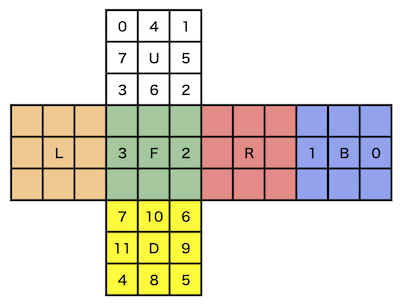
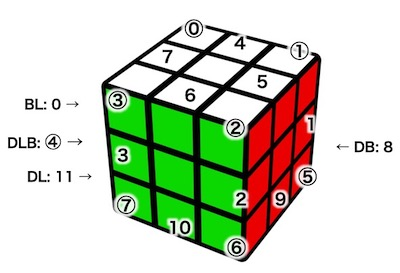
ルービックキューブの状態をプログラム的に扱いやすくするために、下図のようにキューブのパーツに番号を振ります。

• 例えば、0番のコーナーと言ったら、左上後にある白・オレンジ・青のパーツのことを指します
• 例えば、2番のエッジと言ったら、右手前にある緑赤のエッジパーツのことを指します。

パーツのことだけでなく、その位置のことも同じナンバリングで表します。

なので、「1番のコーナーの位置 に 0番のコーナーパーツが入っている」などと言うことがあります。

展開図版ナンバリング説明図

立体版ナンバリング説明図

ルービックキューブの状態を表すクラス

では、実装に入ります。
早速ですが、ルービックキューブの状態を表すクラスを次のように書きました。

class State:
    """
    ルービックキューブの状態を表すクラス
    """
    def __init__(self, cp, co, ep, eo):
        self.cp = cp
        self.co = co
        self.ep = ep
        self.eo = eo

Stateクラスは、cp, co, ep, eo という4つのベクトルを持ちます。
それぞれの意味を説明していきます。

cp

cp は Corner permutation の略でコーナーパーツの場所の情報を表す8次元のベクトルです。
i番目の要素である数字は、i番目のコーナーの位置に現在あるパーツの番号を表します。

例えば、cp が [1,2,0,3,4,5,6,7] というベクトルとき、

• 0番のコーナーの位置 (左上後) に、1番のコーナーパーツ (白青赤のパーツ) が入っている
• 1番のコーナーの位置 (右上後) に、2番のコーナーパーツ (白赤緑のパーツ) が入っている
• 2番の位置に0番のパーツ
• 3番の位置に3番のパーツ
• ……

という状態を表します。

co

co (Corner orientation) は、コーナーがどの向きを向いているかという情報を表す8次元のベクトルです。
先述したように、各コーナーは向きを3通り取ることができます。
"今その位置にあるパーツ" を見て、U面D面色 (白 or 黄色) がU面D面にあるのが0, 時計回りに1つねじれているのが1，反時計回りが2です。

この状態は、1番の位置にあるコーナーが時計回りに、2番の位置にあるコーナー が反時計回りに捻れていて、他のパーツはすべて白 or 黄色が上下に向いています。

そのため、co = [0,1,2,0,0,0,0,0]と表せます。

ep

ep (Edge permutation) はcpと同じ要領でエッジパーツの場所を表した12次元のベクトルです。

eo

eo (Edge orientation) は、エッジがどの向きを向いているかを表す12次元のベクトルです。

先述の、"展開図版ナンバリング説明図"で、数字の書いてある面を基準に、今そこにあるパーツの数字の書いてあった方の色が数字の書いてある面にあれば0, 反転していれば1と表します。
上下にある8パーツは、白 or 黄色 (上 or 下) が基準面で、上下の面に挟まれた中層にある4つのパーツは、緑 or 青 (手前 or 裏)が基準面です。

具体例を挙げると、

これは、eo = [0,0,0,0,0,1,1,0,0,0,0,0]です。
2番の位置にあるエッジは一見反転しているように見えますが、そこに今あるのは、10番のエッジであり、10番のエッジの基準面は黄色(下)、2番の位置の基準面は緑(手前)で、基準面が基準面に収まっているので0 です。

中編以降で出てきますが、EOは、U面, D面, R面, L面をいくら動かしても変化しないという特徴があります。

完成状態の表し方

完成状態は、

• コーナー・エッジともに、0番の位置に0番のパーツ、1番の位置に1番のパーツ、……
• コーナー・エッジともに、全パーツの向きが0

なので、次のように表すことができます。

solved = State(
    [0, 1, 2, 3, 4, 5, 6, 7],
    [0, 0, 0, 0, 0, 0, 0, 0],
    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
)

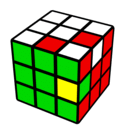
完成状態から R した状態の表し方

具体例を1つ見てみます。完成したルービックキューブを R すると次のような状態になります。

これは、どう表せるでしょうか？
正解は次の通りです。確認してみてください。

r_state = State(
    [0, 2, 6, 3, 4, 1, 5, 7],
    [0, 1, 2, 0, 0, 2, 1, 0],
    [0, 5, 9, 3, 4, 2, 6, 7, 8, 1, 10, 11],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
)

ルービックキューブの操作を表すクラス

ルービックキューブの状態を表すクラスができたので、次に、ルービックキューブの操作を表すクラスを作ります。
と言いたいところですが、これは必要ありません。

ルービックキューブはの操作は先程書いた、Stateクラスで表すことができます。
ルービックキューブの状態と操作は表裏一体です。
完成状態を表す solved_state から操作 R をしたら、別の r_state が得られます。
ということは、別の見方をすれば r_state は R 操作を表現しています。
そのため、操作RはState クラスを使って、

r_move = State(
    [0, 2, 6, 3, 4, 1, 5, 7],
    [0, 1, 2, 0, 0, 2, 1, 0],
    [0, 5, 9, 3, 4, 2, 6, 7, 8, 1, 10, 11],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
)

と表せます。先程定義したr_stateと全く同じものです。
これをどのように操作として解釈するかは後述します。

余談
「状態と操作は別のものなんだから、ちゃんと別のクラスとして定義しろよ横着するな」と思われるかもしれませんが、数学的にもこれでいいのです。
ルービックキューブは群論で表せると聞いたことがある人もいるかもしれません (Wikipediaの記事 群論のinfoboxにもルービックキューブの絵が飾ってありますね)。
群論的に、状態と操作は同じものなのです。

詳しくはSpeedcubing Advent Calendar 2013の12日目の記事 田Φ さんのルービックキューブと数学 を見てください。

ルービックキューブを操作するメソッドを追加する

状態と操作がそれぞれ表せるようになったので、状態に対して操作を適用して、別の状態を返すメソッドを Stateクラスに追加しましょう。

このように apply_move メソッドを書きました。

class State:
    """
    ルービックキューブの状態を表すクラス
    """

    def __init__(self, cp, co, ep, eo):
        self.cp = cp
        self.co = co
        self.ep = ep
        self.eo = eo

    def apply_move(self, move):
        """
        操作を適用し、新しい状態を返す
        """
        new_cp = [self.cp[p] for p in move.cp]
        new_co = [(self.co[p] + move.co[i]) % 3 for i, p in enumerate(move.cp)]
        new_ep = [self.ep[p] for p in move.ep]
        new_eo = [(self.eo[p] + move.eo[i]) % 2 for i, p in enumerate(move.ep)]
        return State(new_cp, new_co, new_ep, new_eo)

引数で受け取っている move が操作を表す State クラスのインスタンスです。

説明のために、具体例を見ましょう。

r_state = State(
    [0, 2, 6, 3, 4, 1, 5, 7],
    [0, 1, 2, 0, 0, 2, 1, 0],
    [0, 5, 9, 3, 4, 2, 6, 7, 8, 1, 10, 11],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
)

r2_state = r_state.apply_move(r_state)
print(f"r2_state.cp = {r2_state.cp}")
print(f"r2_state.co = {r2_state.co}")
print(f"r2_state.ep = {r2_state.ep}")
print(f"r2_state.eo = {r2_state.eo}")

# 出力
r2_state.cp = [0, 6, 5, 3, 4, 2, 1, 7]
r2_state.co = [0, 0, 0, 0, 0, 0, 0, 0]
r2_state.ep = [0, 2, 1, 3, 4, 9, 6, 7, 8, 5, 10, 11]
r2_state.eo = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

先程定義した、r_state を使います。
すでに説明したように r_state は完成状態からRした状態であり、同時に、Rという操作を表しています。

そのため、実装が正しければ、r2_state = r_state.apply_move(r_state) とすると、完成状態からRした状態に更にRを適用した状態、つまり、完成状態からR2をした状態が得られるはずです。

これがR2したキューブの図です。

• 0番のコーナーの位置には、0番のコーナーパーツがあり、coは0 (白か黄色が上)
• 1番のコーナーの位置には、6番のコーナーパーツがある、coは0 (白か黄色が上)
• 2番のコーナーの位置には、5番のコーナーパーツがある、coは0 (白か黄色が上)
• ……

確かにそうなっています。

この具体例を元に、順に実装を見ていきます。

cpの操作

new_cp = [self.cp[p] for p in move.cp]

具体例では、self.cp も move.cpも [0, 2, 6, 3, 4, 1, 5, 7] ですね。

move.cpが表すベクトルを操作として解釈すると

• 新しい0番目には、今0番の位置にあるパーツが来る
  • r_state.cpの0番目の要素は0なので、0のまま
• 新しい1番目には、今2番の位置にあるパーツを持ってくる
  • r_state.cpの2番めの要素は 6 なので、新しく1番の位置に来るのは6番のパーツ
• 新しい2番めには、今6番の位置にあるパーツが来る
  • r_state.cpの6番目の要素は 5 なので新しく、2番の位置に来るのは5番のパーツ
• …

というような具合になって、新しいcpは [0 6 5 3 4 2 1 7]になります。
これの操作をリスト内包表記を使ってnew_cp = [self.cp[p] for p in move.cp]という記述で実装しました。

coの操作

new_co = [(self.co[p] + move.co[i]) % 3 for i, p in enumerate(move.cp)]

具体例では、
self.co と move.co は [0, 1, 2, 0, 0, 2, 1, 0]で、
move.cp は[0, 2, 6, 3, 4, 1, 5, 7]ですね。

coの場合は、操作によってコーナーパーツが移動してしまうので、それも加味しなければいけません。
[self.co[p] for p in move.cp] をすると、[0, 2, 1, 0, 0, 1, 2, 0]が得られます。

これは、cpを加味して、
- 新しく0番の位置に来るパーツ (今の0番の位置) のcoは 0
- 新しく1番の位置に来るパーツ (今の2番の位置) のcoは 2
- ……

という意味です。
新しく i 番目の位置にやってくるパーツのもともとのねじれを取得したわけです。
そして、それが move.co の各要素で指定された分更にねじれるので、
new_co = [self.co[p] + move.co[i] for i, p in enumerate(move.cp)] とします。

これで、[0, 3, 3, 0, 0, 3, 3, 0] が得られます。

コーナーを3回ねじると、元のねじれに戻るので、各要素で3で割った余りを取って [0 0 0 0 0 0 0 0]となります。

実際、白か黄色が上を向いているのが0なので、R2 するとcoは全部 0 に戻りますね。

epの操作

cpと同じなので略

eoの操作

coと同じなので略

1手の操作を全種類定義する

Half Turn Metricでは、"1手" に相当する操作が18種類あります。
それらを全部定義しましょう。

操作の名前 (RやR2など)をkeyとして、その操作に相当するStateクラスのインスタンスを取得できるdictを作ります。

# 18種類の1手操作を全部定義する
moves = {
    'U': State([3, 0, 1, 2, 4, 5, 6, 7],
               [0, 0, 0, 0, 0, 0, 0, 0],
               [0, 1, 2, 3, 7, 4, 5, 6, 8, 9, 10, 11],
               [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]),
    'D': State([0, 1, 2, 3, 5, 6, 7, 4],
               [0, 0, 0, 0, 0, 0, 0, 0],
               [0, 1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 8],
               [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]),
    'L': State([4, 1, 2, 0, 7, 5, 6, 3],
               [2, 0, 0, 1, 1, 0, 0, 2],
               [11, 1, 2, 7, 4, 5, 6, 0, 8, 9, 10, 3],
               [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]),
    'R': State([0, 2, 6, 3, 4, 1, 5, 7],
               [0, 1, 2, 0, 0, 2, 1, 0],
               [0, 5, 9, 3, 4, 2, 6, 7, 8, 1, 10, 11],
               [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]),
    'F': State([0, 1, 3, 7, 4, 5, 2, 6],
               [0, 0, 1, 2, 0, 0, 2, 1],
               [0, 1, 6, 10, 4, 5, 3, 7, 8, 9, 2, 11],
               [0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0]),
    'B': State([1, 5, 2, 3, 0, 4, 6, 7],
               [1, 2, 0, 0, 2, 1, 0, 0],
               [4, 8, 2, 3, 1, 5, 6, 7, 0, 9, 10, 11],
               [1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0]
               )}
move_names = []
faces = list(moves.keys())
for face_name in faces:
    move_names += [face_name, face_name + '2', face_name + '\'']
    moves[face_name + '2'] = moves[face_name].apply_move(moves[face_name])
    moves[face_name + '\''] = moves[face_name].apply_move(moves[face_name]).apply_move(moves[face_name])
print(move_names)

# 出力
['U', 'U2', "U'", 'D', 'D2', "D'", 'L', 'L2', "L'", 'R', 'R2', "R'", 'F', 'F2', "F'", 'B', 'B2', "B'"]

まず、各面を時計回りに90度回す6種類の操作は、Rを書き下したときと同じ要領で、愚直に書き下しました。

180度操作、反時計回り90度操作も同じように書き下しても良いのですが、少し楽をしましょう。
各面について、時計回り90度操作を2回適用すれば180度回す操作、3回適用すれば反時計回り90度操作のStateを得ることができますね。

これで、movesが定義できました。

後で使うので、18種類の全操作名を格納したmove_namesという配列も作っておきました。

スクランブルからStateを作る

各操作が定義できたので、回転記号でルービックキューブの混ぜ方を表した "スクランブル" を元に、Stateクラスのインスタンスを作ることができるようになりました。
やってみましょう。
例題スクランブルとして、
L D2 R U2 L F2 U2 L F2 R2 B2 R U' R' U2 F2 R' D B' F2
を使います。

完成状態からこれを回すと、次の図のような状態が得られるはずです。

# 完成状態を用意
solved_state = State(
    [0, 1, 2, 3, 4, 5, 6, 7],
    [0, 0, 0, 0, 0, 0, 0, 0],
    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
)

# スクランブル
scramble = "L D2 R U2 L F2 U2 L F2 R2 B2 R U' R' U2 F2 R' D B' F2"

# スクランブルを構成する操作を1手ずつ順に適用する
scrambled_state = solved_state
for move_name in scramble.split(" "):
  move_state = moves[move_name]
  scrambled_state = scrambled_state.apply_move(move_state)

# あっているかチェック
print(f"scrambled_state.cp = {scrambled_state.cp}")
print(f"scrambled_state.co = {scrambled_state.co}")
print(f"scrambled_state.ep = {scrambled_state.ep}")
print(f"scrambled_state.eo = {scrambled_state.eo}")

# 出力
scrambled_state.cp = [4, 3, 2, 1, 6, 5, 7, 0]
scrambled_state.co = [0, 0, 1, 0, 2, 2, 2, 2]
scrambled_state.ep = [2, 9, 4, 10, 0, 7, 3, 1, 11, 5, 6, 8]
scrambled_state.eo = [1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0]

特に難しいことはしていません。
スクランブル1手1手に分解し、先程作ったdict moves から操作のStateを引いて、順に適用しているだけですね。

気になる人は、図と見比べて確かめてください。あっているはずです。

スクランブル文字列から、それを適用したStateオブジェクトを得る関数を書いておきます

def scamble2state(scramble):
  """
  スクランブル文字列適用したstateを返す
  """
  scrambled_state = solved_state
  for move_name in scramble.split(" "):
    move_state = moves[move_name]
    scrambled_state = scrambled_state.apply_move(move_state)
  return scrambled_state

次回予告

前編では、ルービックキューブの状態/操作を表現するクラスを作り、状態を操作するメソッドを書きました。

これで、キューブをプログラム的に自由に回せる状態になったので、探索が進められます。

中編では、反復深化深さ優先探索を実装して、キューブを実際に解いてきます。
また、探索の効率をあげて、現実的な時間で探索するために重要な枝刈りについて勉強します。

更新履歴

• 2018/12/14 初版
• 2020/06/19 Numpyを使うとかえって遅いことがわかったので、Numpyに依存しない実装に変更

参考文献

• Solve Rubik's Cube with Cube Explorer
• Computer Puzzling