関数で考える双対性

ベクトルとコベクトルは対等で、役割を入れ替えることができます。これを双対性と呼びます。実例で確認します。NumPyによる計算を添えます。

シリーズの記事です。

1. 見積りで考える内積
2. 関数で考えるコベクトル
3. 関数で考える行列
4. 関数で考える双対性 ← この記事
5. コベクトルで考えるパーセプトロン

NumPyは次のようにインポートしたものとします。

>>> from numpy import *

双対性

以前、次のような表計算を考えました。

品名	単価(A社)	単価(B社)	個数	小計(A社)	小計(B社)
鉛筆	30	25	12	360	300
消しゴム	50	60	10	500	600
ノート	150	120	5	750	600
総計				1,610	1,500

これを計算するため、行列とベクトルを用意します。

>>> A=array([[30,50,150],[25,60,120]]).T
>>> A
array([[ 30,  25],
       [ 50,  60],
       [150, 120]])
>>> X=array([[12,10,5]]).T
>>> X
array([[12],
       [10],
       [ 5]])

A=\left(\begin{matrix} 30 & 25 \\ 50 & 60 \\ 150 & 120 \end{matrix}\right),
X=\left(\begin{matrix} 12 \\ 10 \\ 5 \end{matrix}\right)

表計算と同じ形になっているのに注目してください。左側を転置すれば、順番を入れ替えても同じ数字が得られます。

>>> dot(A.T,X)
array([[1610],
       [1500]])
>>> dot(X.T,A)
array([[1610, 1500]])

A^{\top}X
=\left(\begin{matrix} 30 & 50 & 150 \\ 25 & 60 & 120 \end{matrix}\right)
 \left(\begin{matrix} 12 \\ 10 \\ 5 \end{matrix}\right)
=\left(\begin{matrix} 1610 \\ 1500 \end{matrix}\right) \\
X^{\top}A
=\left(\begin{matrix} 12 & 10 & 5 \end{matrix}\right)
 \left(\begin{matrix} 30 & 25 \\ 50 & 60 \\ 150 & 120 \end{matrix}\right)
=\left(\begin{matrix} 1610 & 1500 \end{matrix}\right) \\

これはベクトルとコベクトルの役割を入れ替えていると解釈します。引数としてベクトルを渡せばベクトルが、コベクトルを渡せばコベクトルが返って来ます。

形式的には全体を転置すると順番が反転して個々に転置するという関係になります。

(A^{\top}X)^{\top}=X^{\top}A

引き算で全体を符号反転すると順序が反転するのに似ていますが、個々に符号反転させれば順番は反転しないのが少し違います。

\begin{align*}
-(3-2)
&=2-3 \\
&=(-3)-(-2)
\end{align*}

入力数・出力数

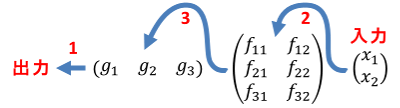
ベクトルとコベクトルでは計算の流れが逆向きになります。

\underbrace{GF}_{合成}
=\overbrace{\left(\begin{matrix}g_1 & g_2 & g_3\end{matrix}\right)}^{入力数3}
 \quad\scriptsize{出力数3}\normalsize{\Biggr\{
  \left(\begin{matrix}f_{11} & f_{12} \\ f_{21} & f_{22} \\ f_{31} & f_{32}\end{matrix}\right)} \\
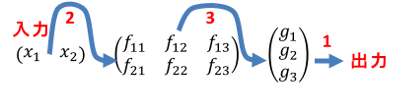
\overbrace{\left(\begin{matrix}f_{11} & f_{12} & f_{13} \\ f_{21} & f_{22} & f_{23} \end{matrix}\right)}^{出力数3}
 \quad\scriptsize{入力数3}\normalsize{\Biggr\{
  \left(\begin{matrix}g_1 \\ g_2 \\ g_3 \end{matrix}\right)}
=\underbrace{FG}_{合成}

間に挟んだ要素数を取り除くと、入力と出力だけが残ります。

\underbrace{1}_{出力}×\underbrace{3←3}_{除去}×\underbrace{2}_{入力} \\
\underbrace{2}_{入力}×\underbrace{3→3}_{除去}×\underbrace{1}_{出力}

計算の流れ

入力と出力を含めた計算の流れを示します。赤い数字は要素数を表します。

値に着目して模式化します。

\underbrace{y}_{出力}
\xleftarrow{G}
\underbrace{\left(\begin{matrix}t_1 \\ t_2 \\ t_3\end{matrix}\right)}_{途中の値}
\xleftarrow{F}
\underbrace{\left(\begin{matrix}x_1 \\ x_2\end{matrix}\right)}_{入力} \\
\underbrace{\left(\begin{matrix}x_1 & x_2\end{matrix}\right)}_{入力}
\xrightarrow{F}
\underbrace{\left(\begin{matrix}t_1 & t_2 & t_3\end{matrix}\right)}_{途中の値}
\xrightarrow{G}
\underbrace{y}_{出力}

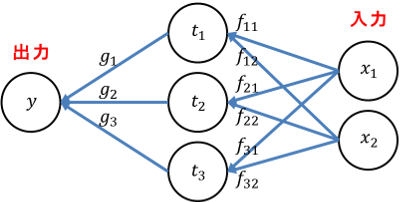
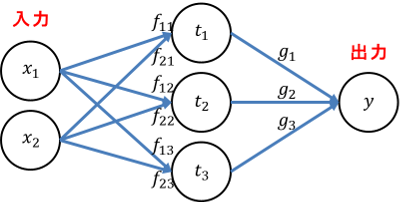
パーセプトロン風に図を描きます。行列表記に合わせて計算の流れを右から左とします。

$t$ と $x$ を結ぶに注目します。このうち $f_{21}$ を例に取れば、添え字を $2←1$ と解釈することで、線が結ぶノード $t_2←x_1$ の添え字に対応することが分かります。模式化すると以下の通りです。

t_2 \xleftarrow{f_{21}} x_1 \\
x_1 \xrightarrow{f_{12}} t_2 \\

他の線も同じパターンになることを確認してください。