Wikipediaのレーベンシュタイン距離のコードの解釈で混乱したため、メモを残します。
レーベンシュタイン距離は文字列の類似度を調べる最も基本的なアルゴリズムです。この記事ではレーベンシュタイン距離そのものの説明はしないで、コードの解釈に集中します。
レーベンシュタイン距離の説明は色々な記事がありますが、分かりやすそうな記事を1つ挙げておきます。
日本語版
まず日本語版のWikipediaを読みます。
次の記述があります。
以下に、文字数
lenStr1の文字列str1と、文字数lenStr2の 文字列str2間のレーベンシュタイン距離を求める擬似コードを示す。このコードにおいてd[i1,i2]には、str1のi1文字目までの文字列とstr2のi2文字目までの文字列の間のレーベンシュタイン距離が格納される。
str1="biting", str2="whiten" のときの配列 d[i1,i2] の様子を部分文字列と共に示します。
| d | i1=0 | i1=1 | i1=2 | i1=3 | i1=4 | i1=5 | i1=6 |
|---|---|---|---|---|---|---|---|
| i2=0 |
0 |
b 1 |
bi 2 |
bit 3 |
biti 4 |
bitin 5 |
biting 6 |
| i2=1 |
w 1 |
b w 1 |
bi w 2 |
bit w 3 |
biti w 4 |
bitin w 5 |
biting w 6 |
| i2=2 |
wh 2 |
b wh 2 |
bi wh 2 |
bit wh 3 |
biti wh 4 |
bitin wh 5 |
biting wh 6 |
| i2=3 |
whi 3 |
b whi 3 |
bi whi 2 |
bit whi 3 |
biti whi 3 |
bitin whi 4 |
biting whi 5 |
| i2=4 |
whit 4 |
b whit 4 |
bi whit 3 |
bit whit 2 |
biti whit 3 |
bitin whit 4 |
biting whit 5 |
| i2=5 |
white 5 |
b white 5 |
bi white 4 |
bit white 3 |
biti white 3 |
bitin white 4 |
biting white 5 |
| i2=6 |
whiten 6 |
b whiten 6 |
bi whiten 5 |
bit whiten 4 |
biti whiten 4 |
bitin whiten 3 |
biting whiten 4 |
※ i1 と i2 の縦横への割り当てには任意性があります。ここではセル内で str1 と str2 を上下に並べたとき、最初の行で見出しと上下に隣接して分かりやすいため i1 を横に割り当てました。あくまで表現上の工夫のため、アルゴリズムの本質には影響しません。
掲載されている擬似コードを見ます。
まず d の1行目と1列目を埋めます。片方が空文字列のため、もう片方の文字列長がそのままレーベンシュタイン距離となります。
for Integer i1 := 0 to lenStr1 do let d[i1,0] := i1 ;
for Integer i2 := 0 to lenStr2 do let d[0,i2] := i2 ;
残りは左から1列ずつ、列内を上から埋めていきます。その際に左 d[i1-1,i2] と上 d[i1,i2-1] と左上 d[i1-1,i2-1] の要素を参照します。
for Integer i1 := 1 to lenStr1 do
for Integer i2 := 1 to lenStr2 do
begin
constant Integer cost := if str1[i1] == str2[i2] then 0 else 1 ;
let d[i1,i2] := minimum
(
d [i1-1, i2 ] + 1, (* 文字の削除 *)
d [i1 , i2-1] + 1, (* 文字の挿入 *)
d [i1-1, i2-1] + cost (* 文字の置換 *)
)
end ;
参照した要素には既に値が入っているのがポイントです。このように依存関係を考慮して計算順序をうまく組み上げる手法を動的計画法と呼びます。
レーベンシュタイン距離を計算するためには、一般的に動的計画法によるアルゴリズムが用いられている。
それぞれの要素がどの要素から由来するかを矢印で示します。
0 |
→ | b 1 |
→ | bi 2 |
→ | bit 3 |
→ | biti 4 |
→ | bitin 5 |
→ | biting 6 |
| ↓ | ↘ | ↘ | ↘ | ↘ | ↘ | ↘ | ||||||
w 1 |
b w 1 |
→ | bi w 2 |
→ | bit w 3 |
→ | biti w 4 |
→ | bitin w 5 |
→ | biting w 6 |
|
| ↓ | ↘ | ↓ | ↘ | ↘ | ↘ | ↘ | ↘ | |||||
|
wh 2 |
b wh 2 |
bi wh 2 |
→ | bit wh 3 |
→ | biti wh 4 |
→ | bitin wh 5 |
→ | biting wh 6 |
||
| ↓ | ↘ | ↓ | ↘ | ↘ | ↘ | |||||||
|
whi 3 |
b whi 3 |
bi whi 2 |
→ | bit whi 3 |
biti whi 3 |
→ | bitin whi 4 |
→ | biting whi 5 |
|||
| ↓ | ↘ | ↓ | ↓ | ↘ | ↘ | ↘ | ||||||
|
whit 4 |
b whit 4 |
bi whit 3 |
bit whit 2 |
→ | biti whit 3 |
→ | bitin whit 4 |
→ | biting whit 5 |
|||
| ↓ | ↘ | ↓ | ↓ | ↓ | ↘ | ↘ | ↘ | |||||
|
white 5 |
b white 5 |
bi white 4 |
bit white 3 |
biti white 3 |
→ | bitin white 4 |
→ | biting white 5 |
||||
| ↓ | ↘ | ↓ | ↓ | ↓ | ↘ | ↓ | ↘ | |||||
|
whiten 6 |
b whiten 6 |
bi whiten 5 |
bit whiten 4 |
biti whiten 4 |
bitin whiten 3 |
→ | biting whiten 4 |
右下の要素が最終的に求めるレーベンシュタイン距離です。右下から矢印を逆にたどると左上までの経路が抽出できます。それを赤字で示しました。
赤字の部分を抽出すると2つの経路が得られます。最初に分岐していますが、その次で合流します。
|
0 |
↓ |
w 1 |
↘ | b wh 2 |
↘ | bi whi 2 |
↘ | bit whit 2 |
↘ | biti white 3 |
↘ | bitin whiten 3 |
→ | biting whiten 4 |
|
0 |
↘ | b w 1 |
↓ | b wh 2 |
↘ | bi whi 2 |
↘ | bit whit 2 |
↘ | biti white 3 |
↘ | bitin whiten 3 |
→ | biting whiten 4 |
コードと比較すれば、左に由来する「→」が削除、上に由来する「↓」が挿入、左上に由来する「↘」が置換とされています。
constant Integer cost := if str1[i1] == str2[i2] then 0 else 1 ;
let d[i1,i2] := minimum
(
d [i1-1, i2 ] + 1, (* 文字の削除 *)
d [i1 , i2-1] + 1, (* 文字の挿入 *)
d [i1-1, i2-1] + cost (* 文字の置換 *)
)
これは str1 を1文字ずつ調べながら変形して str2 を得る操作のコストを表します。このコードで求めているのはあくまでコストであって、文字列の変形は行っていないのに注意が必要です。
変形の過程を表に追加します。「↘」は必ずしも置換するわけではなく、cost が 0 なら何もしません。
| str1 | 挿入 | 置換 | なし | なし | 置換 | なし | 削除 |
|---|---|---|---|---|---|---|---|
| biting | wbiting | whiting | whiting | whiting | whiteng | whiteng | whiten |
| 0 | 1 | 2 | 2 | 2 | 3 | 3 | 4 |
| str1 | 置換 | 挿入 | なし | なし | 置換 | なし | 削除 |
|---|---|---|---|---|---|---|---|
| biting | witing | whiting | whiting | whiting | whiteng | whiteng | whiten |
| 0 | 1 | 2 | 2 | 2 | 3 | 3 | 4 |
部分文字列を示した配列の表において、削除や挿入を行う対象はまた別にあるというのがポイントです。部分文字列だけを見て解釈しようとして、削除の意味が分からずに混乱しました。
配列を解釈しようとする姿勢については次の記事を参考にしました。
グラフ
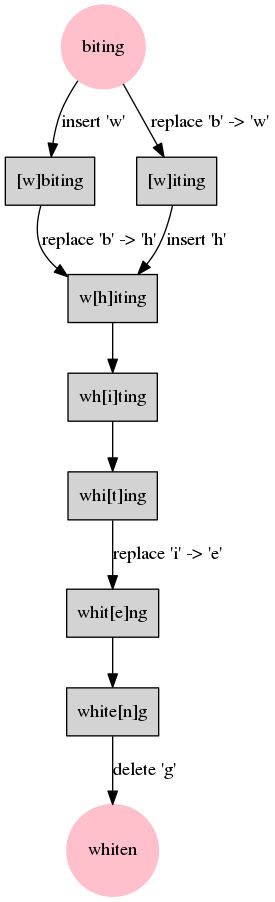
グラフ化することで2つの経路の関係を視覚的に把握することができます。
こちらの記事を参考に手動でグラフを作成してみました。
digraph {
node [shape=record style=filled]
start [label="biting" color=pink shape=circle]
end [label="whiten" color=pink shape=circle]
node1 [label="[w]biting"]
node2 [label="[w]iting"]
node3 [label="w[h]iting"]
node4 [label="wh[i]ting"]
node5 [label="whi[t]ing"]
node6 [label="whit[e]ng"]
node7 [label="white[n]g"]
start -> node1 [label="insert 'w'"]
node1 -> node3 [label="replace 'b' -> 'h'"]
start -> node2 [label="replace 'b' -> 'w'"]
node2 -> node3 [label="insert 'h'"]
node3 -> node4
node4 -> node5
node5 -> node6 [label="replace 'i' -> 'e'"]
node6 -> node7
node7 -> end [label="delete 'g'"]
}
英語版
次に英語版の記事を読みます。
再帰
まず再帰によるC言語のコードが示されます。
// len_s and len_t are the number of characters in string s and t respectively
int LevenshteinDistance(const char *s, int len_s, const char *t, int len_t)
{
int cost;
/* base case: empty strings */
if (len_s == 0) return len_t;
if (len_t == 0) return len_s;
/* test if last characters of the strings match */
if (s[len_s-1] == t[len_t-1])
cost = 0;
else
cost = 1;
/* return minimum of delete char from s, delete char from t, and delete char from both */
return minimum(LevenshteinDistance(s, len_s - 1, t, len_t ) + 1,
LevenshteinDistance(s, len_s , t, len_t - 1) + 1,
LevenshteinDistance(s, len_s - 1, t, len_t - 1) + cost);
}
return の直前のコメントは、文字列の末尾の文字を削って再帰することを説明しています。
以下の記事にはほぼ同じアルゴリズムがPythonで説明されています。末尾ではなく先頭を削って再帰している点が異なりますが、最終的には同じ結果が得られます。
@lru_cache(maxsize=4096)
def ld(s, t):
if not s: return len(t)
if not t: return len(s)
if s[0] == t[0]: return ld(s[1:], t[1:])
l1 = ld(s, t[1:])
l2 = ld(s[1:], t)
l3 = ld(s[1:], t[1:])
return 1 + min(l1, l2, l3)
Wikipediaでは再帰は同じ計算を何度も繰り返すため非効率だとして動的計画法に進みますが、このコードは再帰のままデコレーターによりメモ化しています。前掲の記事ではデコレーターとメモ化について詳しく説明されているため、レーベンシュタイン距離に限らず参考になります。
Wagner–Fischer アルゴリズム
レーベンシュタイン距離を求めるための動的計画法によるアルゴリズムの名前です。
このアルゴリズムによるコードは日本語版のものと基本的に同じです。
if s[i] = t[j]:
substitutionCost := 0
else:
substitutionCost := 1
d[i, j] := minimum(d[i-1, j] + 1, // deletion
d[i, j-1] + 1, // insertion
d[i-1, j-1] + substitutionCost) // substitution
Wikipediaではコードの後に経路が掲載されています。経路に下線が引かれていて、マウスポインタを載せると説明(deleteやinsert)が表示されます。その説明から i が縦(行)で j が横(列)に割り当てられていることが分かります。
2つ例が示されていますが、それぞれ次の組み合わせです。deletionやinsertionは s に対する操作で、最終的に t に変形されます。
-
s="sitting", t="kitten"(削除・置換) -
s="Sunday", t="Saturday"(挿入・置換)
日本語版では縦横は明示されていませんでしたが、自分が理解する際に英語版とは縦横が逆の表を作ったことで混乱してしまいました。
また、Wikipediaでは日本語版と英語版ともに「kitten」を「sitting」に変形する例が示されています。表でも同じ向きの変形かと早合点して s と t を逆に捉えてしまったため、コードの解釈で混乱しました。
- kitten → sitten (substitution of "s" for "k")
- sitten → sittin (substitution of "i" for "e")
- sittin → sitting (insertion of "g" at the end).
英単語
英語版には2つの例が載っていますが、1つの例で3つの操作(削除・挿入・置換)のうち2つしか使っていません。説明の便宜上1つの例で3つの操作を行いたかったため、sittingとkittenを変形して作ったのがbitingとwhitenです。
実在しない単語を使いたくなかったのですが、うまい組み合わせがすぐには思い浮かびませんでした。そのため正規表現で英単語を検索するサイトを利用しました。検索はサーバー側ではなく、圧縮した辞書データを読み込んだクライアント側が行っているようです。
パブリックドメインの英和辞書データを利用しているそうです。
関連記事
レーベンシュタイン距離を利用して機械翻訳の結果から言語系統や精度の確認を行います。
Google スプレッドシートでレーベンシュタイン距離を計算します。
参考
様々な言語によるレーベンシュタイン距離の実装が載っています。