量子力学では非局所性ということが言われます。簡単なプログラムを作って計算で確認してみました。
プログラムで扱うための視点から量子力学や量子コンピューターの世界に入っていくのもありだと思うので、この記事では可能な限り量子力学などの物理の知識を前提としないで説明を試みます。
スピン
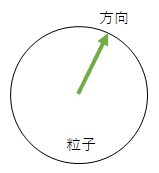
何らかの粒子について考えます。具体的には指定しませんが、電子や光子を想像していただいて構いません。
ここでいう「粒子」は電子やクォークなどの素粒子であっても、ハドロンや原子核や原子など複数の素粒子から構成される複合粒子であってもよい。
粒子はスピンと呼ばれる性質を持っています。今回は単純化して「特定の方向を向いている」と考えます。
測定
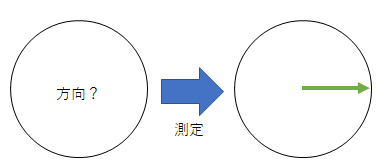
ある方向を指定して、スピンがそちらを向いているかを測定できます。結果は真 (true) か偽 (false) かで得られます。
> 測定(粒子1, 右)
true
> 測定(粒子2, 上)
false
一度測定すると、スピンはその測定で得られた方向を向きます。「右」で true なら右、false なら反対の左です。
測定によって方向が確定するため、何度も同じ測定を繰り返せば同じ結果が得られます。
> 測定(粒子1, 右)
true
> 測定(粒子1, 右)
true
スピンが横方向を向いている状態で縦方向に測定すると、結果はランダムに返ります。
> 測定(粒子1, 右)
true
> 測定(粒子1, 上)
true または false(ランダム)
※ 確率 1/2 のランダムで、制御する方法はありません。物理乱数の生成源としても利用されます。
縦方向の測定によってスピンは上または下を向くようになります。そしてその後にまた横方向の測定をすれば結果はランダムです。
このように測定によってスピンの向きが変わるため、測定前にどちらを向いていたのかは正確には分かりません。
確率
ここまでは上下左右の四方向だけを考えましたが、もちろん斜めを向いていることもあります。
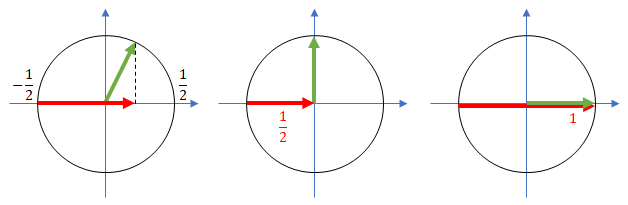
スピンがある方向を向いているときに右だと測定される確率は、直径 1(半径 1/2)の円によって図示できます。スピン方向の円周上の点(緑矢印の先端)から x 軸に垂線を下ろして、円の左端から垂線との交点までの長さが確率です(赤矢印)。スピン方向(緑矢印)が上を向いていれば 1/2、右を向いていれば 1 です。
※ よくある半径 1 の単位円ではないのに注意してください。直径 1 を確率の最大値に対応させています。
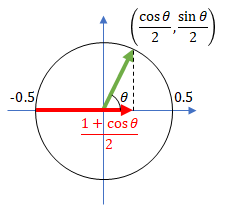
スピン方向(緑矢印)の先の座標は $(\frac{\cosθ}2,\frac{\sinθ}2)$、垂線との交点は $(\frac{\cosθ}2,0)$、円の左端から出ている測定方向の矢印(赤矢印)の長さは $\frac{1+\cosθ}2$ です。
スピン方向(緑矢印)と測定方向(赤矢印)の間の角度 θ が分かれば、どの方向でも確率が計算ができます。
なお、確率は $\cos^2\fracθ2$ と表されることも多いです。
\frac{1+\cosθ}2=\cos^2\fracθ2
実装
角度を指定して確率を求める関数を実装します。
function 確率(θ) {
return (1 + Math.cos(θ / 180 * Math.PI)) / 2;
}
※ θ は度数法で指定します。Math.cos には弧度法(ラジアン)に変換して渡します。度数法の 180° がラジアンの $π$ に対応します。
確率に応じてランダムに 1 か 0 を返す関数を実装します。与えられた確率は 1 になる確率として扱います。
function 測定(確率) {
if (Math.random() < 確率) return 1;
return 0;
}
※ Math.random() は 0 以上 1 未満の乱数を返します。
スピンがランダムな方向を向いている 1,000 個の粒子を、測定方向を固定して測定する例です。測定方向を 0° として、スピンの角度をそのまま確率の計算に回します。
See the Pen 非局所性 (1) by 七誌 (@7shi) on CodePen.
↑ エラーになる場合は一度 CodePen を開いてから、この記事をリロードしてください。
乱数を使っているため多少の誤差は出ますが、平均して半分の 500 回は 1 が出ます。これはランダムに決めた方向が多数の繰り返しによって平均化されるためです。
エンタングルメント
1つの粒子が崩壊して、2つの同種の粒子に分裂したとします。その場合、2つの粒子は正反対の方向に飛んでいきます。
方向だけでなくスピンも正反対の向きとなります。両者を進行方向に対して同じ角度で測定すれば逆の結果が得られます。片方が 1 であれば、もう片方は 0 となります。このような関係性をエンタングルメントや量子もつれと呼びます。
単純にスピンを逆方向にしただけではエンタングルメントは実装できません。
for (let i = 1; i <= 5; i++) {
let spin = Math.random() * 360;
let 測定値1 = 測定(確率(spin));
let 測定値2 = 測定(確率(spin + 180));
log(i, "回目:", 測定値1, ",", 測定値2);
}
1 回目: 0 , 0
2 回目: 0 , 1
3 回目: 1 , 1
4 回目: 1 , 0
5 回目: 0 , 0
所々 0, 0 や 1, 1 のように同じ値が出て来てしまいます。
確実に測定結果を逆にするため、片方の結果を反転させるように特別扱いします。
See the Pen 非局所性 (2) by 七誌 (@7shi) on CodePen.
非局所性
先ほどの例のように両方を同じ角度で測定した場合、崩壊した時点でスピン方向と乱数に相当する何か(隠れた変数)が決まってエンタングルメントが起きるのではないかという疑いがあります。実際、そのように実装することも可能です。
これは大きな論争になりましたが(アインシュタイン=ポドルスキー=ローゼンのパラドックス)、ベルの不等式という確認方法が提案され、最終的に実験によって隠れた変数だけでは説明できない現象が確認されました。(アスペの実験)
つまり空間的に離れた 2 つの粒子の間で何らかのつながり(もつれ)があるということです。これを非局所性と呼びます。非局所性の物理的な仕組みは不明ですが、結果を再現するにはどのように実装するかを考えます。
なお、非局所性の対義語(空間的に離れた粒子のつながりがないこと)は局所性です。
CHSH 実験
非局所性を確認する実験です。アスペの実験もこれです。
左側の粒子を測定する角度を a と a' のどちらか、右側の粒子を測定する角度を b と b' のどちらかとして、4 つの角度はすべて異なるとします。粒子が崩壊して分裂した粒子が測定器に到達するまでの間に、どちらの角度で測定するかをランダムに決めて θ1 と θ2 とします。
崩壊した時点で測定する角度が決まっていないにも関わらず、測定値には角度差に応じた対応が見られます。後で確認しますが、空間的に隔てられたもう一方の測定に使った角度を使わなければ得られない結果です。
測定値は 確率(θ2-θ1) で逆になります。先ほど実装したエンタングルメントの例では θ1 と θ2 が等しいことから 確率(0)=1 より常に逆になります。
実装は次の通りです。spin はスピンの方向です。
function 非局所(spin, θ1, θ2) {
let 測定値1 = 測定(確率(θ1 - spin));
let 測定値2 = 測定値1;
if (Math.random() < 確率(θ2 - θ1)) 測定値2 = 1 - 測定値1;
return [測定値1, 測定値2];
}
測定値2を計算するのに測定値1と θ1 を使っていますが、逆にしても構いません。確率が角度差に依存していることがポイントです。
局所モデルでは崩壊時に乱数を共有していても、角度差が分からないため測定値の傾向は異なります。
function 局所(spin, θ1, θ2) {
let r = Math.random();
let 測定値1 = 0, 測定値2 = 1;
if (r < 確率(θ1 - spin)) 測定値1 = 1;
if (r < 確率(θ2 - spin)) 測定値2 = 0;
return [測定値1, 測定値2];
}
なお、エンタングルメントによるつながりは測定後になくなります。(壊れると表現します)
CHSH 不等式
非局所モデルと局所モデルの違いを調べるのに使うのがベルの不等式です。今回はその一種の CHSH 不等式を使います。ある種の判別式のようなものです。
The usual form of the CHSH inequality is
|S|\leq 2 \tag{1}where
S=E(a,b)-E\left(a,b'\right)+E\left(a',b\right)+E\left(a',b'\right). \tag{2}E = \frac {N_{++} - N_{+-} - N_{-+} + N_{--}} {N_{++} + N_{+-} + N_{-+}+ N_{--}} \tag{3}
数式の細かい説明は EMAN さんの記事に譲って、実装するのに必要な範囲で読み方を説明します。
θ1 と θ2 はランダムに選ぶため毎回変わります。今回は 4 種類の組み合わせがあるので、組み合わせごとに集計すれば傾向が調べられます。(2) の $E(a,b)$ は θ1=a, θ2=b の場合を表し、具体的な計算方法が (3) です。
(3) は測定値の組み合わせの個数から計算します。この記事では測定値を 1 と 0 としましたが、CHSH 不等式では +1 と -1 としており、$N_{++}$ の添え字は測定値の符号を表します。++ と -- は測定値が一致した場合、+- と -+ は一致しない場合で、次のように解釈できます。
E=\frac{\text{一致した個数}-\text{一致しない個数}}{\text{個数の合計}} \tag{3'}
一致と不一致が均衡していれば 0 に近付き、どちらかに偏れば絶対値が大きくなります。
組み合わせの相手を変えても測定値に変化がなければ S の値は (1) の範囲に収まります。絶対値記号を外して書き直します。
-2≦S≦2 \tag{1'}
もしこの範囲からはみ出すようであれば、組み合わせの相手に応じて測定値が変化することを意味します。
理論的に不一致が最大となる角度が示されています。S の値は -2 より小さくなります。
The settings a, a′, b and b′ are generally in practice chosen to be 0, 45°, 22.5° and 67.5° respectively — the "Bell test angles" — these being the ones for which the QM formula gives the greatest violation of the inequality.
👉 a = 0, a' = 45, b = 22.5, b' = 67.5
※ この角度の求め方は、先ほど紹介したEMANさんの記事を参照してください。
実装
CHSH 不等式を実装して S の値を確認します。10,000個の粒子を崩壊させて、生成した粒子を測定します。測定値の一致と不一致を数えて (3') と (2) を計算します。
※ 同じ粒子を 10,000 回測定したのではなく、別々の粒子です。測定によってエンタングルメントが壊れるため、同じ粒子を何度も測定してもエンタングルメントを調べる上では無意味です。
See the Pen 非局所性 (3) by 七誌 (@7shi) on CodePen.
非局所モデルでは -2 を超え、見事に不等式 (1') の範囲からはみ出しました(不等式を破ると表現します)。乱数を共有するだけの局所モデルでは不等式の範囲内に収まっています(たまに誤差程度に少しはみ出します)。これを確認するのが今回の目的でした。
※ 現実の実験では非局所モデルを支持する結果が得られます。
非局所モデルでは角度差だけが S の値に影響するため、spin を固定しても S の値(の傾向)は変化しません。ただし個々の測定値は変化します。局所モデルでは S の値にも影響します。
スピンの振る舞いはすぐには腑に落ちないかもしれません。今回の実装はそれほど難しいことはしていないので、色々といじって結果の変化を確認してみるのも手だと思います。
別実装
非局所モデルでは、最初の測定結果に応じてスピンの方向が確定して、後の測定ではその逆向きが使われると実装しても同じ結果が得られます。
function 非局所(spin, θ1, θ2) {
let 測定値1 = 測定(確率(θ1 - spin));
spin = θ1 + 180 * 測定値1;
let 測定値2 = 測定(確率(θ2 - spin));
return [測定値1, 測定値2];
}
こうすれば測定によってスピンの方向が決まるという考え方が使えて、測定のコードも同じ形になるので分かりやすいかもしれません。ただ、エンタングルメントの影響が角度差に依存していることが読み取りにくいため、先に紹介しませんでした。
【注意】コード中の spin はいわゆる隠れた変数なので、実験的に確認することは不可能です。結果が合うようにしているだけなので、現実を反映している保証は一切ありません。
エンタングルメントと情報
S に現れるのは測定値1と測定値2の関係で、両方を比較して初めてエンタングルメントが検出できます。片方の測定値だけを見てもエンタングルメントによる影響(角度差)は検出できません。
測定値が 1 になる確率を示します。乱数を使っているため多少の誤差は出ますが、非局所・局所のモデルの違いに関係なく平均して半分の 0.5 です。
See the Pen 非局所性 (4) by 七誌 (@7shi) on CodePen.
両方を比較しなければ検出できないのは重要なポイントです。もし片方の測定から角度差に依存した何らかの差異が検出できれば、測定角度を操作することでモールス信号のように情報が送れることになりますが、そういったことは不可能です。つまりエンタングルメントで情報は送れません。エンタングルメントを応用した量子テレポーテーションでも、別手段による通信と併用します。
※ 何かうまい抜け道はないものかと気にはなりますが、それは量子力学に修正を迫るような新発見が必要となるため絶望的です…
ご意見
この記事にいただいたご意見をご紹介します。
これ誤解されそうだけど「量子力学」の非局所性はこれで確認できますが「この世界」の非局所性は古典のプログラムでは確認できません https://t.co/mGS4XDHR8c
— naok1 (@pueeeeeeeb) February 19, 2020
参考
出力の log() は次の実装を使っています。
確率の図示は T. M. さんのツイートが多大なヒントになりました。
ちなみに、この図の赤矢印と青矢印もcos^2(θ/2)、sin^2(θ/2)になります。図形的に確かめることもできると思います。
— T. M. (@myoga33) February 12, 2020
(ブロッホ球の中心と極座標(θ,φ)の点を直径に持つ球を置き、それをXY平面で切ったときの部分球(球欠)の高さがZ軸方向に測定したときの確率を表す、ということもできます) pic.twitter.com/EZvOU9gUXH
CHSH 不等式の基になったベルの不等式については、やはり EMAN さんの記事が参考になります。
同じ話題について少し違ったアプローチで実装する記事です。