前回の記事では独自の簡略化した表記法で計算しました。他の資料への橋渡しとするため、一般的な表記法への書き換えについて説明します。
シリーズの記事です。
- 量子コンピューター超入門
- 量子コンピューター超入門2 一般的な表記法 ← この記事
何を簡略化したのか
前回の記事で、独自の表記法によって簡略化したのは以下の 3 点です。
- ケット
- テンソル積
- 係数
これらを補えば、一般的な表記法に書き換えられます。例を示します。
- H(0)H(1) = (0+1)(0-1) = 00-01+10-11
\mathrm H\ket 0 \otimes \mathrm H\ket 1
=\left(\frac{\ket0+\ket1}{\sqrt2}\right)⊗\left(\frac{\ket0-\ket1}{\sqrt2}\right)
=\frac{\ket{00}-\ket{01}+\ket{10}-\ket{11}}2
数学的な詳細には立ち入らないで、表面的な書き換えとして説明します。
ケット
簡略化では 0, 1 は文字のように扱うとして進めました。これは主に 3 つの理由があります。
- $\ket 0$ のような見慣れない表記による混乱を避ける。
- 扱っているのはビット列の組み合わせである、ということを直観的に伝える。
- 等確率に限定することで係数を排除すれば、数値との混乱は生じない。
係数を省略したままでは高度な計算が行えないため、ある時点でどうしても係数を扱う必要があります。係数と区別するため、ケットと呼ばれる特殊な括弧で基底を表記します。
0 → \ket 0,\ 1 → \ket 1
複数の量子ビットも 1 つのケットの中に入れられます。
01 → \ket{01},\ 110 → \ket{110}
テンソル積
ビット列は並び方に意味があるため、0, 1 の積は順番を入れ替えることができないとして進めました。
- 01 ≠ 10
入れ替えができないことを明示する演算子が $\otimes$ で、これによる積をテンソル積と呼びます。
$$
01 → \ket0\otimes\ket1,\ 110 → \ket1\otimes\ket1\otimes\ket0
$$
既に出て来た複数桁をケットに入れる表記法は、テンソル積を簡略化したものです。こちらも一般的に用いられます。
$$
\ket0\otimes\ket1=\ket{01},\ \ket1\otimes\ket1\otimes\ket0=\ket{110}
$$
テンソル積によって順番が縛られるのは基底 $\ket0, \ket1$ だけです。係数は普通の積と同じように扱います。
$$
2\ket 0\otimes3\ket 1=6\ket{01}
$$
係数
係数の 2 乗は、測定によってその基底の表す値が現れる確率です。
$$
\ket0=1\ket0:\ 1^2=1=100\%
$$
0 と 1 が 50% ずつ現れる場合、それぞれ 1/2 の平方根となります。
$$
\frac{1}{\sqrt2}\ket0+\frac{1}{\sqrt2}\ket1:\ \left(\frac1{\sqrt 2}\right)^2=\frac12=50\%
$$
係数を付けることで、等確率でない重ね合わせ状態が記述できます。例えば 0 が 25%、1 が 75% の確率で現れる重ね合わせ状態を示します。
$$
\frac{1}2\ket0+\frac{\sqrt3}2\ket1
$$
係数が確率そのものではなく、確率の平方根であることは、最初は奇妙に思えます。後で図示しますが、平方根にすれば 2 乗の和が 1 になることから、単位円上の一点に収まるため計算しやすくなります。
$$
x^2+y^2=1
$$
計算しやすくなる例を挙げます。
- H(0+1) = H(0)+H(1) = (0+1)+(0-1) = 0+0+1-1 = 0
\begin{aligned}
\mathrm H\left(\frac{\ket0+\ket1}{\sqrt2}\right)
&=\frac{\mathrm H\ket0+\mathrm H\ket1}{\sqrt2} \\
&=\frac{\frac{\ket0+\ket1}{\sqrt2}+\frac{\ket0-\ket1}{\sqrt2}}{\sqrt2} \\
&=\frac{\ket0+\ket0+\ket1-\ket1}2 \\
&=\ket0
\end{aligned}
係数が確率そのものであれば、このような計算が成り立たなくなります。
また、この計算を見ると、H が項ごとに作用するのは、単に掛け算として分配されているように見えます。実際、H は行列、ケットはベクトルとして表現できるため、積として分配されます。
量子状態を完全に表現するには、行列やベクトルの成分は複素数である必要があります。今回は複素数には踏み込まず、実数の範囲内に限定します。
確率とテンソル積
2 つの量子ビット $a,b$ を考えます。
\begin{aligned}
\ket a &= \sqrt{\frac13}\ket0+\sqrt{\frac23}\ket1 \\
\ket b &= \sqrt{\frac14}\ket0+\sqrt{\frac34}\ket1
\end{aligned}
係数を 2 乗すれば確率が求まります。
| 0 | 1 | |
|---|---|---|
| a | 1/3 | 2/3 |
| b | 1/4 | 3/4 |
$a,b$ の組み合わせの確率は、掛け合わせることで得られます。(赤字部分)
| b=0 | b=1 | ||
|---|---|---|---|
| 1/4 | 3/4 | ||
| a=0 | 1/3 | 1/12 | 3/12 |
| a=1 | 2/3 | 2/12 | 6/12 |
テンソル積の計算は、この表と同じことをしています。
\begin{aligned}
\ket a\otimes\ket b
&=\left(\sqrt{\frac13}\ket0+\sqrt{\frac23}\ket1\right)\otimes\left(\sqrt{\frac14}\ket0+\sqrt{\frac34}\ket1\right) \\
&=\sqrt{\frac1{12}}\ket{00}+\sqrt{\frac3{12}}\ket{01}+\sqrt{\frac2{12}}\ket{10}+\sqrt{\frac6{12}}\ket{11}
\end{aligned}
書き換えの例
ここまでの内容で、前回の計算を一般的な表記法に書き換えることができます。
量子テレポーテーションの計算を示します。
x: x - - - - - C - H - - - - - C - - -
| |
a: 0 - H - C - X - - - C - - - | - - -
| | |
b: 0 - - - X - - - - - X - H - X - H -
前回は係数を避けるため x を状態ごとに場合分けして計算しました。今回は場合分けせずに係数 $\alpha,\beta$ で計算します。ケットの中にはラベルが書かれるため、$\ket x$ は量子状態を表す変数です。($\vec x$ と同じ考え方)
\ket x=\alpha\ket0+\beta\ket1\quad(\alpha^2+\beta^2=1)
係数を実数に限定しています。複素数に拡張した場合、条件は $|\alpha|^2+|\beta|^2=1$ となります。
\begin{aligned}
\ket{x00}
=&(\alpha\ket0+\beta\ket1)⊗\ket 0⊗\ket 0 \\
\xrightarrow{\mathrm I⊗\mathrm H⊗\mathrm I}
&(\alpha\ket0+\beta\ket1)⊗\left(\frac{\ket0+\ket1}{\sqrt2}\right)⊗\ket 0 \\
=&\frac{(\alpha\ket0+\beta\ket1)⊗(\ket{00}+\ket{10})}{\sqrt2} \\
\xrightarrow{\mathrm I⊗\mathrm{CX}}
&\frac{(\alpha\ket0+\beta\ket1)⊗(\ket{00}+\ket{11})}{\sqrt2} \\
=&\frac{\alpha(\ket{000}+\ket{011})+\beta(\ket{100}+\ket{111})}{\sqrt2} \\
\xrightarrow{\mathrm{CX}⊗\mathrm I}
&\frac{\alpha(\ket{000}+\ket{011})+\beta(\ket{110}+\ket{101})}{\sqrt2} \\
=&\frac{\alpha\ket0⊗(\ket{00}+\ket{11})+\beta\ket1⊗(\ket{10}+\ket{01})}{\sqrt2} \\
\xrightarrow{\mathrm H⊗\mathrm I⊗\mathrm I}
&\frac{\alpha\left(\frac{\ket0+\ket1}{\sqrt2}\right)⊗(\ket{00}+\ket{11})+\beta\left(\frac{\ket0-\ket1}{\sqrt2}\right)⊗(\ket{10}+\ket{01})}{\sqrt2} \\
&\frac{\alpha(\ket0+\ket1)⊗(\ket{00}+\ket{11})+\beta(\ket0-\ket1)⊗(\ket{10}+\ket{01})}2 \\
\xrightarrow{\mathrm I⊗\mathrm{CX}}
&\frac{\alpha(\ket0+\ket1)⊗(\ket{00}+\ket{10})+\beta(\ket0-\ket1)⊗(\ket{11}+\ket{01})}2 \\
=&\frac{\alpha(\ket0+\ket1)⊗(\ket0+\ket1)⊗\ket0+\beta(\ket0-\ket1)⊗(\ket{1}+\ket{0})⊗\ket1}2 \\
\xrightarrow{\text{C-(HXH)}}
&\frac{\alpha(\ket0+\ket1)⊗(\ket0+\ket1)⊗\ket0+\beta(\ket0+\ket1)⊗(\ket{1}+\ket{0})⊗\ket1}2 \\
=&\left(\frac{\ket0+\ket1}{\sqrt2}\right)⊗\left(\frac{\ket0+\ket1}{\sqrt2}\right)⊗(\alpha\ket0+\beta\ket1)
\end{aligned}
矢印の上はゲートによる操作を表しますが、C-(HXH) は数学的な表記ではなく、ラベルとして書いています。
見た目はいきなり難しくなりましたが、本質的には前回と同じです。係数の扱いに注意すれば、後は表記法の違いです。是非、前回の記事と見比べながら計算を追ってみてください。
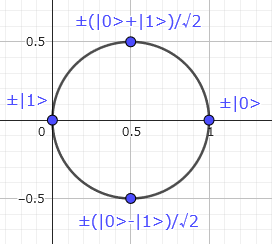
図形的な意味
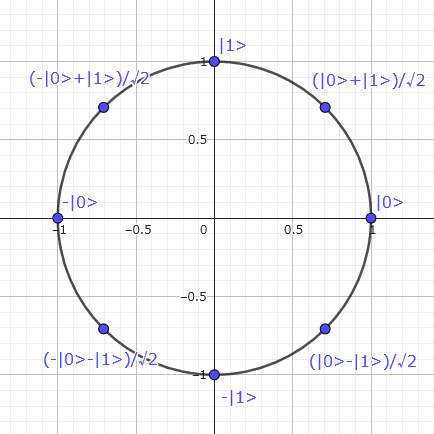
$\ket0,\ket1$ の係数を $x,y$ とおけば、単位円上の点となります。
$$
x\ket0+y\ket1\quad(x^2+y^2=1)
$$
係数を実数に限定しています。複素数に拡張すれば単位超球面上の点となりますが、詳細は機会を改める予定です。
前回の記事で扱った 8 つの状態を示します。
このように視覚化すれば、基底状態の中間に重ね合わせ状態があることが明確になります。
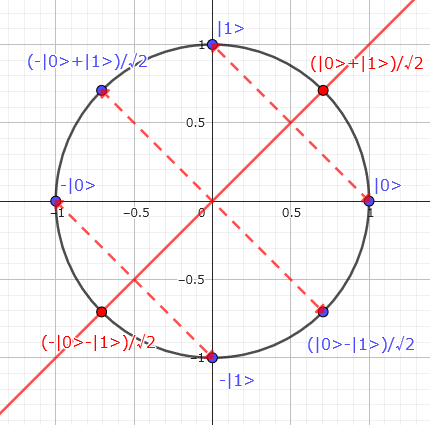
X ゲート
X ゲートは $\ket 0$ と $\ket1$ の中点と原点を通る線に対する鏡映です。
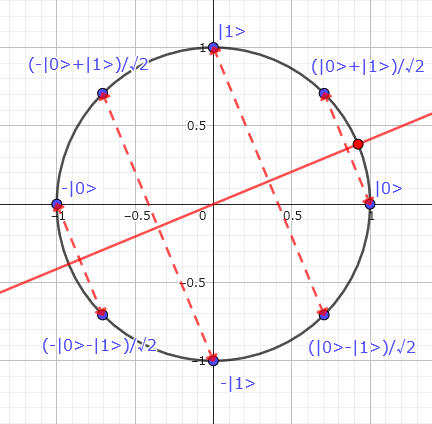
H ゲート
H ゲートは $\ket0$ と $(\ket0+\ket1)/\sqrt2$ の中点と原点を通る線に対する鏡映です。
確率の視覚化
単位円は角度でパラメーター表示できます。
$$
(x,y)=(\cos\theta,\sin\theta)
$$
確率は係数の 2 乗です。x,y を 2 乗してプロットすれば、(1,0) と (0,1) を結ぶ線分になります。
$$
(x^2,y^2)=(\cos^2\theta,\sin^2\theta)=(\cos^2\theta,1-\cos^2\theta)
$$
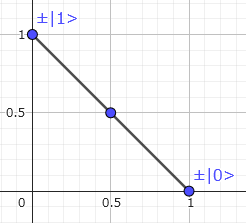
これでは潰れて情報量が少な過ぎます。少しひねって $(x^2,xy)$ を考えます。
この座標は外積(ベクトル積とは別の演算)で正当化できます。詳細は機会を改めます。
半角の公式には cos の 2 乗が現れます。
$$
\cos^2\frac{\theta}2=\frac{1+\cos\theta}2
$$
導出については金沢工業大学さんのサイトが詳しいです。添えられた図が味わい深いです。
角度を 2 倍にすれば、$x^2$ に適用できます。
$$
x^2=\cos^2\theta=\frac{1+\cos{2\theta}}2
$$
2 倍角の公式を逆に適用して、$xy$ も $2\theta$ で表します。
$$
xy=\cos\theta\sin\theta=\frac{\sin2\theta}2
$$
以上より、$(x^2,xy)$ は半径 1/2 の円になります。
$$
(x^2,xy)=\left(\frac{1+\cos{2\theta}}2,\frac{\sin{2\theta}}2\right)
$$
$θ$ で表される元の円の 1 周が、$2θ$ で表される円では 2 周になります。それにより量子状態における符号の違いが区別されなくなりました。x 座標は 2 乗によりマイナスが消えたため常に 0 以上で、確率をダイレクトに表します。
流れの都合上、量子状態を $\theta$ で表しました。ただし、観測される角度を基準にして、量子状態の方を $\theta/2$ で表すことが一般的です。
電子のスピンという性質で量子ビットを実装したとき、$\ket 0$ と $\ket 1$ は反対方向として観測されるため、この図のような位置関係になります。詳細は以下の記事を参照してください。
おわりに
前回の簡略化した表記法を一般的に使われる表記法に書き換え、図形的な意味を説明しました。
何度も断ったように、本来は複素数で表される係数を実数に制限しているため、まだ先があります。実数から複素数に拡張すれば何が変わるかという視点で、続編を構想中です。