link > Python で 1 変量データ補間 > SciPy > interpolate.*

動作環境

GeForce GTX 1070 (8GB)
ASRock Z170M Pro4S [Intel Z170chipset]
Ubuntu 16.04 LTS desktop amd64
TensorFlow v1.2.1
cuDNN v5.1 for Linux
CUDA v8.0
Python 3.5.2
IPython 6.0.0 -- An enhanced Interactive Python.
gcc (Ubuntu 5.4.0-6ubuntu1~16.04.4) 5.4.0 20160609
GNU bash, version 4.3.48(1)-release (x86_64-pc-linux-gnu)
scipy v0.19.1
geopandas v0.3.0

一次関数の補間が気になりだした。

Python関連で一次補間を比較しているコード例を以下に見つけた。
Python で 1 変量データ補間 by かくあきさん

情報感謝です。

code

Matplotlibコード

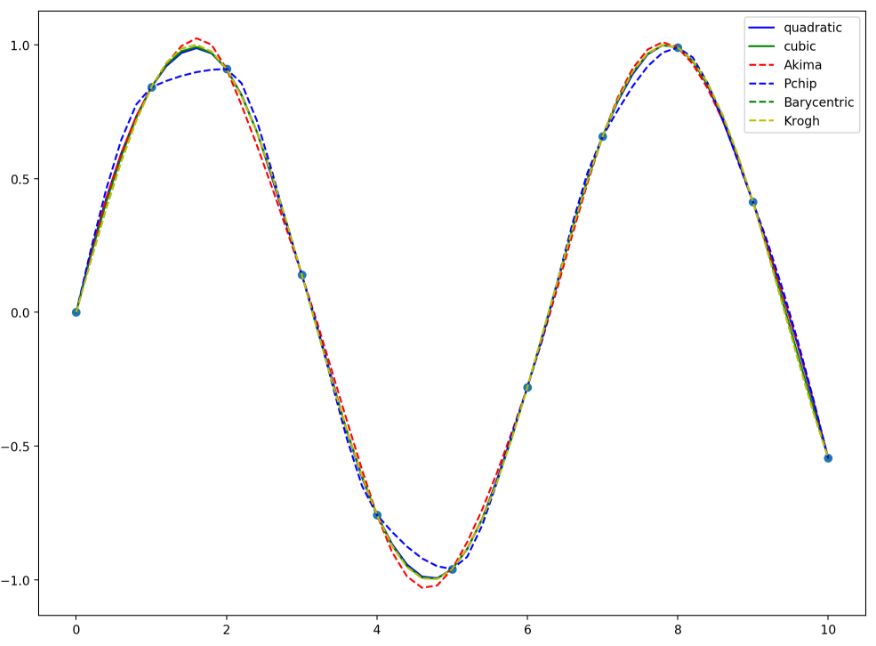
描画の中で自分が使いたい補間処理だけを表示するようにコードを変更してみた(表示部分のコメントアウト)。
また、図の表示がこちらの環境では小さいようなので、dpi変更をした。

Interpolate_171028.ipynb

import numpy as np
from scipy import signal, interpolate
from matplotlib import pylab as plt


# forked from 
# https://org-technology.com/posts/univariate-interpolation.html
# 謝辞: かくあきさん
#

# サンプルデータ作成
t = np.linspace(0, 10, 11)
tt = np.linspace(0, 10, 51)
y = np.sin(t)

# 線形補間
f1 = interpolate.interp1d(t, y)
y1 = f1(tt)

# 2 次スプライン補間
f2 = interpolate.interp1d(t, y, kind="quadratic")
y2 = f2(tt)

# 3 次スプライン補間
f3 = interpolate.interp1d(t, y, kind="cubic")
y3 = f3(tt)

# 1 次スプライン補間(線形補間と結果は同じ)
f4 = interpolate.interp1d(t, y, kind="slinear")
y4 = f4(tt)

# 0 次スプライン補間
f5 = interpolate.interp1d(t, y, kind="zero")
y5 = f5(tt)

# 最近傍点による補間
f6 = interpolate.interp1d(t, y, kind="nearest")
y6 = f6(tt)

# 秋間法による補間
f7 = interpolate.Akima1DInterpolator(t, y)
y7 = f7(tt)

# 区分的 3 次エルミート補間
# y8 = interpolate.pchip_interpolate(t, y, tt)でも結果は同じ
f8 = interpolate.PchipInterpolator(t, y)
y8 = f8(tt)

# 重心補間
# y9 = interpolate.barycentric_interpolate(t, y, tt)でも結果は同じ
f9 = interpolate.BarycentricInterpolator(t, y)
y9 = f9(tt)

# Krogh により提案された補間法
# y10 = interpolate.Krogh_interpolate(t, y, tt)でも結果は同じ
f10 = interpolate.KroghInterpolator(t, y)
y10 = f10(tt)

plt.figure(figsize=(12, 9),dpi=200)
plt.plot(t, y, "o")
# plt.plot(tt, y1, "r", label="linear")
plt.plot(tt, y2, "b", label="quadratic")
plt.plot(tt, y3, "g", label="cubic")
# plt.plot(tt, y4, "y", label="slinear")
# plt.plot(tt, y5, "m", label="zero")
# plt.plot(tt, y6, "c", label="nearest")
plt.plot(tt, y7, "--r", label="Akima")
plt.plot(tt, y8, "--b", label="Pchip")
plt.plot(tt, y9, "--g", label="Barycentric")
plt.plot(tt, y10, "--y", label="Krogh")
plt.legend()
plt.show()

検索用キーワード

• 一次補間
• cubic interpolation