Jupyter + Matplotlib > 横軸のtickを30刻みにする > plt.xticks(np.arange(0, 180 + 1, 30)) | 教えていただいた事項: Matplotlibのインタフェースの流儀(二つ) | ax.set_xticks() | Locator: 軸の表示範囲に応じて対応

動作環境

GeForce GTX 1070 (8GB)
ASRock Z170M Pro4S [Intel Z170chipset]
Ubuntu 16.04 LTS desktop amd64
TensorFlow v1.2.1
cuDNN v5.1 for Linux
CUDA v8.0
Python 3.5.2
IPython 6.0.0 -- An enhanced Interactive Python.
gcc (Ubuntu 5.4.0-6ubuntu1~16.04.4) 5.4.0 20160609
GNU bash, version 4.3.48(1)-release (x86_64-pc-linux-gnu)
scipy v0.19.1
geopandas v0.3.0
MATLAB R2017b (Home Edition)
ADDA v.1.3b6

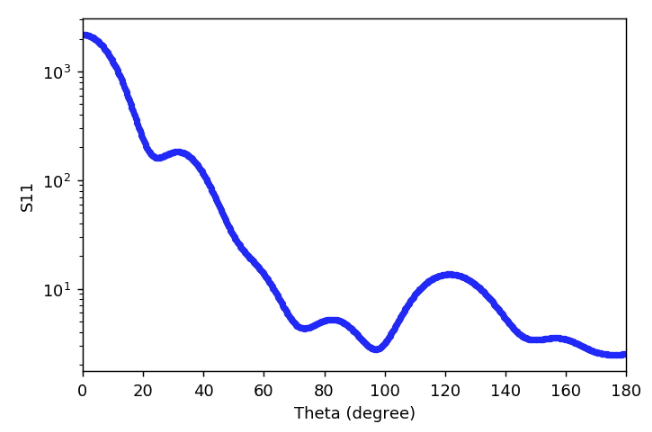
横軸のtickを30刻みにしたい。

https://stackoverflow.com/questions/12608788/changing-the-tick-frequency-on-x-or-y-axis-in-matplotlib
を参考に以下にすればよさそうだ。

plt.xticks(np.arange(0, 180 + 1, 30))

code

読込みファイル

mueller(一部)

theta s11 s12 s13 s14 s21 s22 s23 s24 s31 s32 s33 s34 s41 s42 s43 s44
0.00 2.1910026245E+03 -3.8774638144E+02 -1.9779979218E-14 -1.0841870903E-13 -3.8774638144E+02 2.1910026245E+03 -1.1517862800E-13 -1.3515860232E-13 -7.5528113459E-14 1.5837758333E-13 2.0766651624E+03 5.8103962671E+02 -1.1849195172E-13 1.1853050125E-13 -5.8103962671E+02 2.0766651624E+03
0.25 2.1902574222E+03 -3.8771611257E+02 9.1430802256E-14 -7.2257893126E-14 -3.8771611257E+02 2.1902574222E+03 3.4802617464E-14 -2.6090153053E-13 6.3061675877E-14 2.5044104239E-14 2.0759309444E+03 5.8087391532E+02 -1.4261071510E-13 2.8175773275E-13 -5.8087391532E+02 2.0759309444E+03
0.50 2.1879816315E+03 -3.8766614453E+02 -1.0763739836E-14 1.8916604537E-15 -3.8766614453E+02 2.1879816315E+03 2.4190212015E-13 9.7275761615E-15 3.2395568801E-14 -2.3758458952E-13 2.0736745278E+03 5.8038998343E+02 -5.2525568607E-15 5.5878887331E-14 -5.8038998343E+02 2.0736745278E+03
0.75 2.1841795739E+03 -3.8759596104E+02 -1.9793994203E-14 -5.0695045135E-14 -3.8759596104E+02 2.1841795739E+03 1.8580092598E-13 -2.3380177050E-13 -1.2363164168E-14 -1.1184455334E-13 2.0699001687E+03 5.7958871054E+02 -9.3812328036E-14 2.8752018848E-13 -5.7958871054E+02 2.0699001687E+03
1.00 2.1788584647E+03 -3.8750467893E+02 1.1962588546E-14 -4.2456725516E-13 -3.8750467893E+02 2.1788584647E+03 -5.8262511526E-14 -8.6064524008E-14 -1.1903146887E-13 9.9226630487E-14 2.0646149751E+03 5.7847155283E+02 -4.3086292387E-13 1.4271156369E-13 -5.7847155283E+02 2.0646149751E+03
1.25 2.1720283935E+03 -3.8739105269E+02 1.3972516044E-13 -2.3824530300E-13 -3.8739105269E+02 2.1720283935E+03 4.6889946324E-13 1.8012544371E-14 1.5407225070E-13 -4.7651082444E-13 2.0578288875E+03 5.7704053954E+02 -2.9127961150E-13 1.5945757499E-13 -5.7704053954E+02 2.0578288875E+03
1.50 2.1637022973E+03 -3.8725348076E+02 2.7103031680E-13 -2.5373531025E-13 -3.8725348076E+02 2.1637022973E+03 -3.0808365865E-13 -4.9696733660E-13 1.1713906146E-13 4.0300194526E-13 2.0495546531E+03 5.7529826784E+02 -3.9464666266E-13 4.5946709814E-13 -5.7529826784E+02 2.0495546531E+03
1.75 2.1538959258E+03 -3.8709001362E+02 3.0422323851E-13 -1.2064780244E-13 -3.8709001362E+02 2.1538959258E+03 -6.4719724915E-14 -6.4763347232E-13 2.2115024580E-13 1.9391153871E-13 2.0398077924E+03 5.7324789642E+02 -3.1244569970E-13 6.5225619799E-13 -5.7324789642E+02 2.0398077924E+03
2.00 2.1426277993E+03 -3.8689836361E+02 -1.4106946955E-13 6.9896820129E-14 -3.8689836361E+02 2.1426277993E+03 -4.1160500097E-14 -7.4172035517E-14 -1.2977569832E-13 8.2166754248E-14 2.0286065582E+03 5.7089313755E+02 9.6200954063E-14 4.1886714513E-14 -5.7089313755E+02 2.0286065582E+03
2.25 2.1299191589E+03 -3.8667591653E+02 -1.8188977623E-13 -3.8915376389E-13 -3.8667591653E+02 2.1299191589E+03 -2.0792239148E-14 1.8002928605E-13 -2.8006451197E-13 2.2494396182E-14 2.0159718879E+03 5.6823824784E+02 -2.9767761363E-13 -1.2190329387E-13 -5.6823824784E+02 2.0159718879E+03
2.50 2.1157939104E+03 -3.8641974477E+02 2.8125131981E-13 -1.0652004024E-13 -3.8641974477E+02 2.1157939104E+03 -2.9105786970E-13 1.1551957765E-13 1.9965532282E-13 2.0806568885E-13 2.0019273486E+03 5.6528801766E+02 -1.4665775390E-13 -1.6028114765E-13 -5.6528801766E+02 2.0019273486E+03
2.75 2.1002785597E+03 -3.8612662211E+02 8.3449010379E-14 2.0088538736E-13 -3.8612662211E+02 2.1002785597E+03 -3.6262753136E-14 7.0072589578E-13 1.6648230525E-13 -1.8382739869E-13 1.9864990754E+03 5.6204775923E+02 3.0149180334E-13 -7.2789713905E-13 -5.6204775923E+02 1.9864990754E+03
3.00 2.0834021433E+03 -3.8579304004E+02 -6.1167930982E-14 2.2872473673E-13 -3.8579304004E+02 2.0834021433E+03 -2.3088224347E-13 2.5113856614E-14 -3.6954070408E-14 2.1839390503E-13 1.9697157032E+03 5.5852329342E+02 2.5732346353E-13 -1.3328865525E-13 -5.5852329342E+02 1.9697157032E+03
3.25 2.0651961502E+03 -3.8541522545E+02 6.0980650405E-14 -5.7144629355E-14 -3.8541522545E+02 2.0651961502E+03 4.4591216692E-15 -3.3755383623E-14 4.2864577278E-14 -3.1465783844E-15 1.9516082924E+03 5.5472093534E+02 -7.9320520591E-14 4.7899658853E-14 -5.5472093534E+02 1.9516082924E+03
3.50 2.0456944394E+03 -3.8498915985E+02 -2.5463333817E-13 8.1495824734E-14 -3.8498915985E+02 2.0456944394E+03 -3.9772690682E-13 -7.1651004494E-14 -3.0365317583E-13 4.5209568607E-13 1.9322102474E+03 5.5064747869E+02 1.5854203834E-13 -6.9218294163E-14 -5.5064747869E+02 1.9322102474E+03
3.75 2.0249331495E+03 -3.8451059966E+02 1.8189098700E-13 -5.0096486110E-13 -3.8451059966E+02 2.0249331495E+03 -2.1243791301E-13 -4.4678387562E-13 -2.5332322430E-14 3.2589241500E-13 1.9115572309E+03 5.4631017905E+02 -6.1330844055E-13 4.8091441946E-13 -5.4631017905E+02 1.9115572309E+03
4.00 2.0029506044E+03 -3.8397509788E+02 2.9879089149E-13 -3.1374548488E-14 -3.8397509788E+02 2.0029506044E+03 -1.7723666015E-14 -4.4774864928E-13 2.5641194229E-13 8.8663853359E-14 1.8896870709E+03 5.4171673591E+02 -1.9774101674E-13 4.5554356223E-13 -5.4171673591E+02 1.8896870709E+03
4.25 1.9797872119E+03 -3.8337802676E+02 -3.0611855108E-13 -8.0923057747E-13 -3.8337802676E+02 1.9797872119E+03 -2.2113871894E-13 -4.2768970583E-13 -5.9314583984E-13 4.3934085860E-13 1.8666396635E+03 5.3687527383E+02 -7.7552506645E-13 4.9345602502E-13 -5.3687527383E+02 1.8666396635E+03
4.50 1.9554853580E+03 -3.8271460146E+02 6.9106087981E-14 -1.7533687067E-14 -3.8271460146E+02 1.9554853580E+03 -6.0323278886E-14 -3.1296812931E-13 3.3859183829E-14 1.3532155009E-13 1.8424568700E+03 5.3179432243E+02 -9.3391853961E-14 2.9675145687E-13 -5.3179432243E+02 1.8424568700E+03
4.75 1.9300892966E+03 -3.8197990459E+02 2.6135533537E-13 -2.3040990383E-13 -3.8197990459E+02 1.9300892966E+03 3.0751036016E-13 -3.4189807342E-13 2.3110947170E-13 -2.4199820114E-13 1.8171824100E+03 5.2648279562E+02 -3.8355260298E-13 4.8168728124E-13 -5.2648279562E+02 1.8171824100E+03
5.00 1.9036450340E+03 -3.8116891162E+02 4.5105632826E-14 -4.5404509201E-13 -3.8116891162E+02 1.9036450340E+03 -1.7854020406E-13 -4.1493159265E-13 -1.4395950977E-13 3.1033743262E-13 1.7908617494E+03 5.2094996975E+02 -5.2907713634E-13 4.4742709117E-13 -5.2094996975E+02 1.7908617494E+03
5.25 1.8762002101E+03 -3.8027651680E+02 4.0614076284E-14 -4.1624411860E-13 -3.8027651680E+02 1.8762002101E+03 -3.3408745983E-13 -3.9930914534E-13 -1.6893840665E-13 4.5791851986E-13 1.7635419848E+03 5.1520546112E+02 -4.7958438828E-13 3.8079594905E-13 -5.1520546112E+02 1.7635419848E+03
5.50 1.8478039754E+03 -3.7929755971E+02 4.1225526614E-13 -6.4866901309E-13 -3.7929755971E+02 1.8478039754E+03 -7.7979795462E-13 -2.0350648495E-14 5.9405380137E-14 7.2572242428E-13 1.7352717243E+03 5.0925920264E+02 -7.1261742562E-13 -4.9524370743E-14 -5.0925920264E+02 1.7352717243E+03
5.75 1.8185068646E+03 -3.7822685228E+02 2.4611038005E-13 3.0665220998E-13 -3.7822685228E+02 1.8185068646E+03 -1.6352903080E-13 3.5513544944E-13 3.1802168874E-13 -1.0977993557E-14 1.7061009647E+03 5.0312141984E+02 3.1180299379E-13 -4.4327803850E-13 -5.0312141984E+02 1.7061009647E+03
6.00 1.7883606679E+03 -3.7705920598E+02 2.1752468755E-13 -2.4518831813E-13 -3.7705920598E+02 1.7883606679E+03 2.3515980832E-13 -2.0310768852E-13 1.7825100551E-13 -2.0155533430E-13 1.6760809659E+03 4.9680260622E+02 -3.6014031811E-13 3.3161496415E-13 -4.9680260622E+02 1.6760809659E+03
6.25 1.7574182995E+03 -3.7578945932E+02 2.5712808035E-13 3.8146466952E-13 -3.7578945932E+02 1.7574182995E+03 -1.3904882189E-13 -3.1270920780E-13 3.1506077875E-13 1.5005025497E-13 1.6452641233E+03 4.9031349813E+02 2.4215055111E-13 2.0217958454E-13 -4.9031349813E+02 1.6452641233E+03

Jupyter code

showMueller_180113.ipynb

%matplotlib inline
import matplotlib.pyplot as plt
from matplotlib import cm, colors
from mpl_toolkits.mplot3d import Axes3D
from pylab import rcParams
import numpy as np
import time


"""
v0.1 Jan. 13, 2018
   - set x axis ticks to 30 degree
   - show [S11] as a function of [Theta]
"""

# Coding rule:PEP8

# rcParams['figure.figsize'] = 10, 7
rcParams['figure.dpi'] = 130

IN_FILE = 'mueller'  # obtained from ADDA

# read from file
dat = np.genfromtxt(IN_FILE, delimiter=' ', skip_header=1)
thetas = []
s11s = []
for elem in dat:
    thetas += [elem[0]]
    s11s += [elem[1]]

# plot
fig = plt.figure()
ax1 = fig.add_subplot(1, 1, 1)
ax1.set_yscale('log')
ax1.set_xlabel('Theta (degree)')
ax1.set_ylabel('S11')
ax1.set_xlim(0, 180)

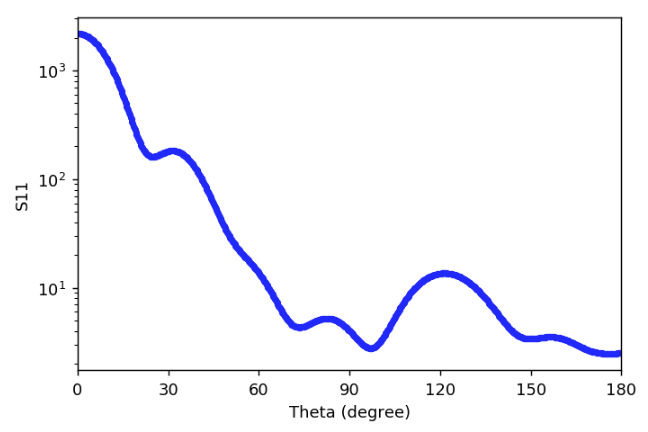
plt.xticks(np.arange(0, 180 + 1, 30))

ax1.scatter(thetas, s11s, color='blue', marker='.')

備考

• np.arange()を使う場合、+1しないと180が表示されない
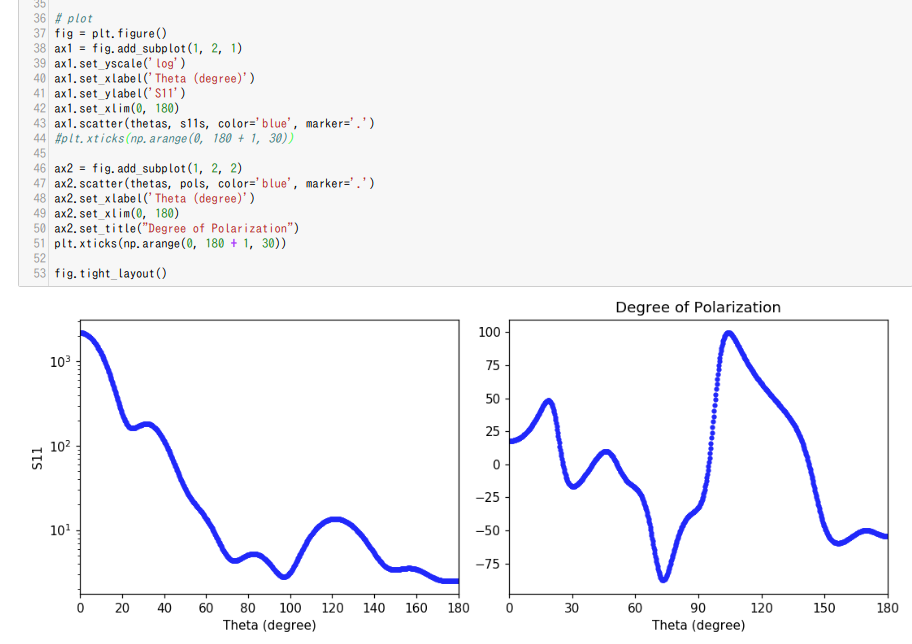
• 2つのfig.add_subplot()がある場合、それぞれに対してplt.xticks()をコールしないと片方だけの設定変更になる (下図)?

留意事項

ax.set_xlim(150, 180)を実行した後にplt.xticks(np.arange(0, 180 + 1, 30))とすると、X軸の最小値は0になる。
両者の最小値を合わせて指定しないといけない。

教えていただいた事項

@skotaro さんのコメントにおいて下記の事項を教えていただきました。
情報感謝です。

• Matplotlibのインタフェースの流儀(二つ)
• ax.set_xticks():link
• Locator
  • 軸の表示範囲に応じて対応
  • Locator以外: 静的な変更になる