Hartree-Fock法の変分法の基礎について簡単にまとめました。
また、一次元の箱の中の粒子で実際に数値計算してみました。
理論面に重点をおいています。
 こんなの作ります。
こんなの作ります。
この記事は量子化学を意識してHartree-Fock法の基礎として変分法をまとめています。オイラー方程式とかは知らないです。あと、論理的に巡回していないかなどは考えていません。
まえがき
身の回りの物質は原子、分子からできています。そして原子、分子の性質はシュレディンガー方程式で記述されます。
つまりシュレディンガー方程式が解ければ、物質の性質を計算で予測することができます。
しかし少し問題があって、シュレディンガー方程式は複雑なため簡単には解けません。なのでシュレディンガー方程式を近似して解くことになります。原子、分子についてのシュレディンガー方程式の近似の方法のひとつにHartree-Fock法という近似方法があります。
Hartree-Fock法に関するQiitaの記事は、
Yuki Sakamoto(@YukiSakamoto@github)さんの 量子化学計算コードを自作してみた記録 その1、
@dc1394 さんのできるだけ簡単にHartree-Fock法を解説してみる(C++17のコード付き)
があり、詳しく記述されています。
このHartree-Fock法は変分法を基礎として、電子多体系の問題を解いています。で、このHartree-Fock法を私もコーディングしてみようと思ったのですが、Hartree-Fock法の基礎となる変分法がよくわからなかずつまずきました。調べていく中である程度理解することができたため、この記事で変分法についてまとめました。
あらすじ
この記事では 1.時間依存しないシュレディンガー方程式、2.変分方程式、3.Ritzの変分法、4.箱の中の粒子の4つについて触れます。もう少し詳しく書くと
時間依存しない定常状態のシュレディンガー方程式は $$ H \psi = E \psi \tag{1} $$ で
じつは、 $ H \psi = E \psi $は $\phi$についての変分方程式
E(\phi)=\frac{\int\phi^{*}H\phi dv}{\int\phi^{*}{\phi}dv} \tag{2}
が極小となるとき、つまり $\delta E =0 $ とすると導けることを示します。つまり(2)を解けば(1)が解けます。
Rizの変分法といって(2)の変分方程式
E(\phi)=\frac{\int\phi^{*}H\phi dv}{\int\phi^{*}{\phi}dv} \tag{2}
に $ \phi =\sum_{k=0}^{n}c_n f_n $ を代入して数値的に解く方法の説明をします。
一次元の箱の中の粒子では $ H \psi = E $ は
\begin{eqnarray*}
( \frac{d^2}{d x^2}+V(x) ) \psi(x) &=& E \psi(x) \tag{3} \\ \\
V(x) &=& \left\{
\begin{array}{ll}
0 & (|x|< 1) \\
\infty & (|x|\geqq 1)
\end{array}
\right.
\end{eqnarray*}
となります。この場合について変分法で解きます。
1.時間依存しないシュレディンガー方程式
時間発展するシュレディンガー方程式は、一般的に
$$i\hbar\frac{\partial}{\partial t} \psi(x,t) = H \psi(x,t) $$
とかけますが、今回は無限大のポテンシャルで囲まれた一次元の箱の中の粒子を考えるため、時間依存しないシュレディンガー方程式
$$ H \psi(x) = E \psi(x) $$
を考えます。
変分原理
この$ H \psi = E \psi $は $\phi$についての変分方程式
E(\phi)=\frac{\int\phi^{*}H\phi dv}{\int\phi^{*}{\phi}dv} \tag{2.0}
が停留する、 $\delta E (\phi) =0 $ とすると導けることを示します[1]。解の存在と極値が停留点となることは仮定します。(また$\phi$としてはとりあえずヒルベルト空間上の関数を考えます。)
まず、$(2.0)$の$\phi$を$\phi + \delta \phi$で置き換えると
\begin{eqnarray*}
E(\phi) + \delta E(\phi) &=& \frac{\int(\phi^{*}+\delta\phi^{*}) H(\phi+\delta\phi) dv}{\int(\phi^{*}+\delta\phi^{*})(\phi+\delta\phi) dv} \\ \\
&=& \frac{ (\int \phi^{*} H\phi dv
+ \int\phi^{*} H \delta \phi dv
+ \int\delta\phi^{*} H\phi dv)}{ (\int \phi^{*} \phi dv
+ \int\phi^{*} \delta \phi dv
+ \int\delta\phi^{*} \phi dv)}\\ \\
&=&\frac{\int \phi^{*} H\phi dv
+ \int\phi^{*} H \delta \phi dv
+ \int\delta\phi^{*} H\phi dv}{ \int \phi^{*} \phi dv (1+\cfrac{\int\phi^{*} \delta \phi dv}{\int \phi^{*} \phi dv}+\cfrac{\int\delta\phi^{*} \phi dv}{\int \phi^{*} \phi dv})} \\ \\
&=& \frac{\int \phi^{*} H\phi dv
+ \int\phi^{*} H \delta \phi dv
+ \int\delta\phi^{*} H\phi dv}{ \int \phi^{*} \phi dv } (1-\cfrac{\int\phi^{*} \delta \phi dv}{\int \phi^{*} \phi dv}-\cfrac{\int\delta\phi^{*} \phi dv}{\int \phi^{*} \phi dv})\\ \\
&=& \frac{\int \phi^{*} H\phi dv
}{ \int \phi^{*} \phi dv } - \frac{\int \phi^{*} H\phi dv
}{ \int \phi^{*} \phi dv }(\cfrac{\int\delta\phi^{*} \phi dv}{\int \phi^{*} \phi dv} + c.c.)
+ (\frac{\int\delta\phi^{*} H \phi dv }{\int \phi^{*} \phi dv } +c.c. ) \\ \\ \\
&=& E(\phi)
- E(\phi)(\cfrac{\int\delta\phi^{*} \phi dv}
{\int \phi^{*} \phi dv}
+ c.c.)
+(\frac{\int\delta\phi^{*} H \phi dv }{\int \phi^{*} \phi dv } +c.c. ) \tag{2.1}\\\
\end{eqnarray*}
と変形できます。式変形を説明しておきます。一行目から二行目では2次の微小項を無視して展開しました。三行目から四行目では$\cfrac{1}{1+x}=1-x $としました。四行目から五行目ではもう一度2次の微小項を無視して展開しました。また$c.c.$ は複素共役(complex conjugate)を表しています。
先程の式$(2.1)$の左辺と最後の行から$E(\phi)$を引くと
\delta E (\phi) = - E(\phi)(\cfrac{\int\delta\phi^{*} \phi dv}{\int \phi^{*} \phi dv} + c.c.) +(\frac{\int\delta\phi^{*} H \phi dv }{\int \phi^{*} \phi dv } +c.c. )
$E(\phi)$を積分の中に入れてやると
\delta E (\phi) =\cfrac{\int\delta\phi^{*} (H-E(\phi)) \phi dv}{\int \phi^{*} \phi dv} + c.c.
となります。
で、任意の$\delta \phi$に対して、$\delta E(\phi)=0$となるためには、
$$ H\phi=E(\phi)\phi$$
が必要かつ十分(ぶっちゃけここよくわからないので誰か教えて...)。よって、(1)の式が導けました。
リッツの変分法(Ritz Variational Method)
前の項目で、
E(\phi)=\frac{\int\phi^{*}H\phi dv}{\int\phi^{*}{\phi}dv} \tag{2.0}
を極小化してやれば、$ H=E(\phi)$ が成り立つことを説明しました。なので、$E(\phi)$を極小化する関数$\phi$を見つけてきて極値$E(\phi)$を計算すれば$ H=E(\phi)$ を解いたことになります。リッツの変分法とは、この$E(\phi)$を極小化する関数$\phi$をみつける方法の一つです。
まず、適当な関数の集合$f_n$をとってきます。この$f_n$は試行関数と呼ばれます。$f_n$の条件としては、今回の問題では、境界条件をみたしていること、互いに線形独立であること、${ f_n }$ が完全系をなすこと、$\int f^{*}_n H f_n dv $ が計算しやすいことなどが挙げられます。
そして、これら関数の線形結合で$\phi$を表します
\phi=\sum_{k=0}^{N}c_kf_k \tag{3.0}
(もう少し厳密に「これら関数の線形結合で$\phi$を表します」を詳しく述べると、「「任意の$\epsilon > 0$に対して、$|\phi-\sum_{k=0}^{N}c_kf_k|<\epsilon$をみたす自然数$N$が存在する」と仮定する」となります。)
何をやろうとしているのかというと、$\phi$を変幻自在に変えて$E(\phi)$の変化をみることは難しくてできないから、まず$f_k$を固定し、係数$c_k$だけを変えてやったときの$E(\phi)$を考えようとしてます。
$\sum$の範囲は$n=\infty$としても色々考えられるようですが、今回は数値計算のための方法を考えたいので、Nは正の整数とします。この$\phi=\sum_{k=0}^{n}c_kf_k$を$(2.0)$に代入してやりたいのですが、見やすくするために
\begin{eqnarray*}
H_{mn}&=&\int f_m^{*}H f_n dv \\
S_{mn}&=&\int f_m^{*} f_n dv
\end{eqnarray*} \tag{3.1}
として、$(2.0)$に代入してやると、
\begin{eqnarray*}
E(\{c_k\})=\frac{\sum_{m=0}^{N}\sum_{n=0}^{N}c^{*}_mc_nH_{mn}}{\sum_{m=0}^{N}\sum_{n=0}^{N}c^{*}_mc_nS_{mn}}\tag{3.2}
\end{eqnarray*}
となります。いま$f_k$は固定して考えているので当然$H_{mn}$、$S_{mn}$も固定されています。なので$E(\phi)$の値は$f_n$の係数${c_k}$のみに依存します。なので、$E(\phi)$を$E({c_k})$としました。言い換えれば、${c_k}$のみが$E$の変数です。
変分原理の項で述べた「任意の$\delta E(\phi)$に対して、$\delta E(\phi)=0$」に対応する条件は、
\frac{\partial E(\{c_k\})}{\partial c^{*}_i}=0 \ \ (i=0,1,...,N) \tag{3.3}
つまり
\frac{\partial E(\{c_k\})}{\partial c^{*}_i}=\frac{\partial}{\partial c^{*}_i} \left( \frac{\sum_{m=0}^{N}\sum_{n=0}^{N}c^{*}_mc_nH_{mn}}{\sum_{m=0}^{N}\sum_{n=0}^{N}c^{*}_mc_nS_{mn}}\right) =0 \tag{3.4}
です。複素共役での偏微分に疑問を感じる方もいらっしゃるかと思いますが、ウィルティンガーの微分のように複素数の微分を定義してやれば、複素数とその複素共役をそれぞれ独立変数のように偏微分できること、また線型性や合成関数の微分のチェインルールも保障されています。
$(3.4)$の左辺を積の微分法${ f(x)g(x) }^{′}=f′(x)g(x)+f(x)g′(x)$や合成関数の微分法を使って式変形します。
\begin{eqnarray*}
\frac{\partial}{\partial c^{*}_i} \left( \frac{\sum_{m=0}^{N}\sum_{n=0}^{N}c^{*}_mc_nH_{mn}}{\sum_{m=0}^{N}\sum_{n=0}^{N}c^{*}_mc_nS_{mn}}\right)
&=& \frac{\sum_{n=0}^{N}c_nH_{in}}{\sum_{m=0}^{N}\sum_{n=0}^{N}c^{*}_mc_nS_{mn}} - \frac{\sum_{m=0}^{N}\sum_{n=0}^{N}c^{*}_mc_nH_{mn}\sum_{n=0}^{N}c_nS_{in}}{(\sum_{m=0}^{N}\sum_{n=0}^{N}c^{*}_mc_nS_{mn})^2}\\ \\
&=&\frac{\sum_{n=0}^{N}c_nH_{in}}{\sum_{m=0}^{N}\sum_{n=0}^{N}c^{*}_mc_nS_{mn}} - \frac{\sum_{m=0}^{N}\sum_{n=0}^{N}c^{*}_mc_nH_{mn}}{\sum_{m=0}^{N}\sum_{n=0}^{N}c^{*}_mc_nS_{mn}}\frac{\sum_{n=0}^{N}c_nS_{in}}{\sum_{m=0}^{N}\sum_{n=0}^{N}c^{*}_mc_nS_{mn}}\\ \\
&=&\frac{\sum_{n=0}^{N}c_nH_{in}}{\sum_{m=0}^{N}\sum_{n=0}^{N}c^{*}_mc_nS_{mn}} - E(\{c_k\})\frac{\sum_{n=0}^{N}c_nS_{in}}{\sum_{m=0}^{N}\sum_{n=0}^{N}c^{*}_mc_nS_{mn}}\\ \\
&=&\frac{\sum_{n=0}^{N}(H_{in}-E(\{c_k\})S_{in})c_n}{\sum_{m=0}^{N}\sum_{n=0}^{N}c^{*}_mc_nS_{mn}}\tag{3.5}\\ \\
\end{eqnarray*}
これが$0$となるので、$c_n \ (n=0,1,...,N)$についての連立方程式
\sum_{n=0}^{N}(H_{in}-E(\{c_k\})S_{in})c_n = 0 \ \ (i=0,1,...,N)\tag{3.6}
が得られました。これは
\sum_{n=0}^{N}H_{in}c_n = E(\{c_k\})\sum_{n=0}^{N}S_{in}c_n\ \ \ (i=0,1,...,N)\tag{3.7}
とも書け、一般化固有値問題になっています。
行列を使って表示すると
\left(\begin{array}{cccc}
H_{11} & H_{12} & \ldots & H_{1N} \\
H_{21} & H_{22} & \ldots & H_{2N} \\
\vdots & \vdots & \ddots & \vdots \\
H_{N1} & H_{N2} & \ldots & H_{NN}
\end{array}
\right)=
E(\{c_k\})
\left(\begin{array}{cccc}
S_{11} & S_{12} & \ldots & S_{1N} \\
S_{21} & S_{22} & \ldots & S_{2N} \\
\vdots & \vdots & \ddots & \vdots \\
S_{N1} & S_{N2} & \ldots & S_{NN}
\end{array}
\right)
\left(
\begin{array}{c}
c_1 \\
c_2 \\
\vdots \\
c_N
\end{array}
\right)\tag{3.8}
です。
一般化固有値問題の解法についてはpythonの数値計算ライブラリscipyが解いてくれるので、解説しません。コレスキー分解とかなんか色々やってくれて解けるみたいです。
ここまでのリッツの変分法を数式3行にまとめると変分問題
E(\phi)=\frac{\int\phi^{*}H\phi dv}{\int\phi^{*}{\phi}dv} \tag{2.0}
を極小化する関数$\phi$を見つけるためには、$\phi$を既知の関数$f_k$の線形結合
\phi=\sum_{k=0}^{N}c_kf_k \tag{3.0}
で近似したとき$c_k$を決めればよく、次の一般化固有値問題に帰着でき、これを解けば$\phi$の近似解$\sum_{k=0}^{N}c_kf_k $と$E(\phi)$の近似解$E({c_k})$が求まる。
\left(\begin{array}{cccc}
H_{11} & H_{12} & \ldots & H_{1N} \\
H_{21} & H_{22} & \ldots & H_{2N} \\
\vdots & \vdots & \ddots & \vdots \\
H_{N1} & H_{N2} & \ldots & H_{NN}
\end{array}
\right)
\left(
\begin{array}{c}
c_1 \\
c_2 \\
\vdots \\
c_N
\end{array}
\right)
=
E(\{c_k\})
\left(\begin{array}{cccc}
S_{11} & S_{12} & \ldots & S_{1N} \\
S_{21} & S_{22} & \ldots & S_{2N} \\
\vdots & \vdots & \ddots & \vdots \\
S_{N1} & S_{N2} & \ldots & S_{NN}
\end{array}
\right)
\left(
\begin{array}{c}
c_1 \\
c_2 \\
\vdots \\
c_N
\end{array}
\right)\tag{3.8}
変分原理の項をもとにすると$$ H\phi=E(\phi)\phi$$がなりたつのは$E(\phi)$が極小になるときなので、$\phi$を$\phi$の近傍にある関数$\sum_{k=0}^{N}c_kf_k$で置き換えた、
\begin{eqnarray*}
E(\{c_k\})=\frac{\sum_{m=0}^{N}\sum_{n=0}^{N}c^{*}_mc_nH_{mn}}{\sum_{m=0}^{N}\sum_{n=0}^{N}c^{*}_mc_nS_{mn}}\tag{3.2}
\end{eqnarray*}
は$E(\phi)\leqq E({c_k})$を満たします。
実装
一次元の箱の中の粒子でリッツの変分法を実装します。
一次元の箱の中の粒子では時間に依存しないシュレーディンガー方程式は $ H \psi = E $ は
\begin{eqnarray*}
( \frac{d^2}{d x^2}+V(x) ) \psi(x) &=& E \psi(x) \tag{3} \\ \\
V(x) &=& \left\{
\begin{array}{ll}
0 & (|x|< 1) \\
\infty & (|x|\geqq 1)
\end{array}
\right.
\end{eqnarray*}
試行関数$f_n$として多項式$x^n (x-1)(x+1)\ \ (n=0,1, ...,N)$を用います[1]。この関数は下の図のようになっていて(レイアウト崩れててごめんなさい)
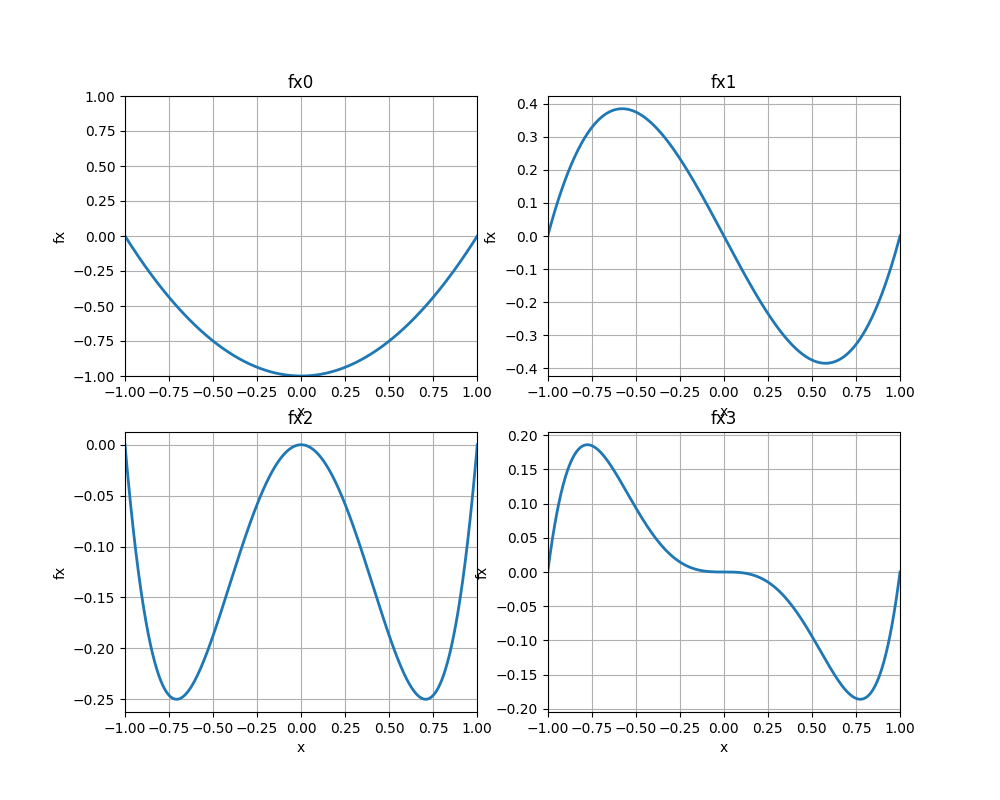
境界条件を満たしていること、原点に関して対称または反対称になっていることがわかります。境界条件、ポテンシャルも$-1<x<1$の範囲内で反対称ですから、こいつらは試行関数としてうまくやってくれるだろうと期待できます。(たぶんやろうと思えばストーン=ワイエルシュトラスの定理でこの試行関数の完全性などを証明できるかと思いますが、めんどくさいのでやらないです。)
で、この試行関数を用いた時のハミルトニアンの行列、重なり積分の行列の各成分
\begin{eqnarray*}
H_{mn}&=&\int f_m^{*}H f_n dv \\
S_{mn}&=&\int f_m^{*} f_n dv
\end{eqnarray*} \tag{3.1}
は
$m+n=2k \ (k \in \mathbb{N}) $ のとき($k=0$つまり$m=n=0$のときも含む)
\begin{eqnarray*}
H_{mn}&=&-8 \left[ \frac{1-m-n-2mn}{(m+n+3) (m+n+1) (m+n-1)} \right] \\
S_{mn}&=& \frac{2}{n+m+5} +\frac{4}{n+m+3}+ \frac{2}{n+m+1}
\end{eqnarray*} \tag{3.1}
$m+n=2k+1 \ (k \in \mathbb{N}) $のとき
\begin{eqnarray*}
H_{mn}&=&0 \\
S_{mn}&=&0
\end{eqnarray*}
です。あとは一般化固有値問題
\sum_{n=0}^{N}H_{in}c_n = E(\{c_k\})\sum_{n=0}^{N}S_{in}c_n\ \ \ (i=0,1,...,N)\tag{3.7}
を解くプログラムを書けば完成です。
import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt
import numpy as np
import scipy.linalg as lin
# Making matrix
def overlap(I,J):
i = I
j = J
if (i+j) % 2 == 0:
return (2/(i+j+5)) - (4/(i+j+3)) + (2/(i+j+1))
else:
return 0
def hermiltonian(I,J):
i = I
j = J
if (i+j) % 2 == 0:
return -8*(1-i-j-2*i*j) /((i+j+3)*(i+j+1)*(i+j-1))
else:
return 0
size_matrix = 6
overlap_array = [[] for i in range(size_matrix)]
hermiltonian_array = [[] for i in range(size_matrix)]
for n in range(size_matrix):
for m in range(size_matrix):
overlap_array[n].append(overlap(n,m))
hermiltonian_array[n].append(hermiltonian(n,m))
# Solving eigenvalue problem
eigen_value,eigen_vector = lin.eigh(hermiltonian_array, overlap_array)
# plotting
x = np.linspace(-1,1,50)
def trial_function(c,n):
return c * x**n * (x+1) * (x-1)
solution = np.zeros(50)
for i in range(size_matrix):
solution += trial_function(eigen_vector[0][i],i)
plt.plot(x,solution)
plt.savefig("n_0.png")
出力として、同じディレクトリにn_0.pngという名前の
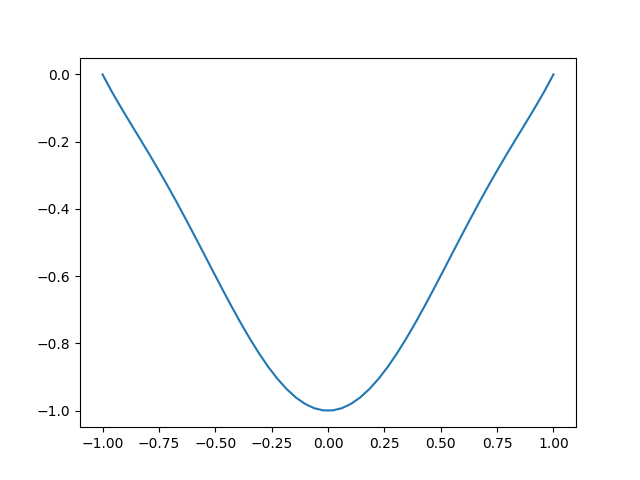
のような画像ファイルが保存されます。
上のコードの変数size_matrixが$f_n$の個数を表しています。上のコードではsize_matrix = 6なので、$ f_0, \ \ f_1, \ \ f_2, \ \ f_3, \ \ f_4, \ \ f_5, $の6個の関数の線型結合で近似しています。
考察
上のコードのsize_matrixをいろいろ変えてみて、固有値$E({ c_k })$の変化をみます。
| size | $E_1$ | $E_2$ | $E_3$ | $E_4$ | $E_5$ | $E_6$ |
|---|---|---|---|---|---|---|
| 3 | 2.467437405 | 10.5 | 25.53256259 | |||
| 4 | 2.467437405 | 9.875388203 | 25.53256259 | 50.1246118 | ||
| 5 | 2.467401109 | 9.875388203 | 22.29340591 | 50.1246118 | 87.73919298 | |
| 6 | 2.467401109 | 9.869618349 | 22.29340591 | 39.99797889 | 87.73919298 | 142.6324028 |
| 12 | 2.4674011 | 9.869604401 | 22.20660991 | 39.47841793 | 61.68624765 | 88.83601306 |
| 18 | 2.4674011 | 9.869604401 | 22.2066099 | 39.4784176 | 61.68502751 | 88.82643962 |
| analytical | 2.4674011 | 9.869604401 | 22.2066099 | 39.4784176 | 61.6850275 | 88.8264396 |
どの変分法の解$E_n$も解析解を超えていないことが確認できます。変分原理で仮定していた
極値が停留点であることがあるていど確かめられました。
またsizeつまり試行関数の数が多いほど、解析解に近づいており、もう一つの仮定「「任意の$\epsilon > 0$に対して、$|\phi-\sum_{k=0}^{N}c_kf_k|<\epsilon$をみたす自然数$N$が存在する」と仮定する」もあるていどは確かめられました。
いちおうコードも上げときます。
import csv
import numpy as np
import scipy.linalg as lin
# Making matrix
def overlap(I,J):
i = I
j = J
if (i+j) % 2 == 0:
return (2/(i+j+5)) - (4/(i+j+3)) + (2/(i+j+1))
else:
return 0
def hermiltonian(I,J):
i = I
j = J
if (i+j) % 2 == 0:
return -8*(1-i-j-2*i*j) /((i+j+3)*(i+j+1)*(i+j-1))
else:
return 0
def energy_analytical(n):
return (n*3.1415926535/2)**2
list_size_matrix = [3,4,5,6,12,18]
list_eigen_value = []
for k, size_matrix in enumerate(list_size_matrix):
# making matrix
overlap_array = [[] for i in range(size_matrix)]
hermiltonian_array = [[] for i in range(size_matrix)]
for n in range(size_matrix):
for m in range(size_matrix):
overlap_array[n].append(overlap(n,m))
hermiltonian_array[n].append(hermiltonian(n,m))
# Solving eigenvalue problem
eigen_value,eigen_vector = lin.eigh(hermiltonian_array, overlap_array)
list_eigen_value.append(eigen_value.tolist())
# Comparing approximate E values and analytical E values
list_exact_E = [energy_analytical(i+1) for i in range(6)]
list_eigen_value.append(list_exact_E)
print(list_eigen_value)
with open('E_value.csv', 'w') as file:
writer = csv.writer(file, lineterminator='\n')
writer.writerows(list_eigen_value)
ちなみにこのコードでは試行関数を増やしすぎるsize_matrix>30くらいにすると、有効桁の関係で対称性が崩れて計算ができなくなってしまいます。[4]
参考文献
[1] Numerical Methods in Quantum Mechanics
[2] Jos Thijssen, Computational Physics second edition( Cambridge University Press 2007)
[3] Linus Pauling, E. Bright Wilson Jr. , Introduction to Quantum Mechanics with Applications to Chemistry (Dover Books on Physics 1985)
[4] 励起状態の変分法計算
[5] 変分原理-Wikipedia
[6] [ウィルティンガーの微分-Wikipedia][https://ja.wikipedia.org/wiki/%E3%82%A6%E3%82%A3%E3%83%AB%E3%83%86%E3%82%A3%E3%83%B3%E3%82%AC%E3%83%BC%E3%81%AE%E5%BE%AE%E5%88%86]