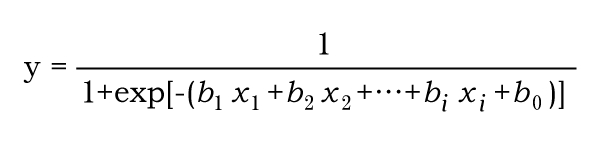#ロジスティック回帰とは
Wikipediaによると
ロジスティック回帰はベルヌーイ分布に従う変数の統計的回帰モデルの一種である。
ベルヌーイ分布とは確率pで1を、確率q=1-pで0をとる、離散確率分布である。
0 でない確率をとる確率変数値がある程度数えられる個数である確率分布のこと。
また、ロジスティック回帰は、一般化線形モデルの一種である。
一般化線形モデルは、残差を任意の分布とした線形モデル。残差とは誤差の推定量。
まずロジスティック回帰とは、ある事象が発生する確率を予測する式を作ることです
重回帰分析との違いは、重回帰分析は目的変数が連続値なのに対し
ロジスティック回帰は目的変数が二値です
二値とはある事象が起こる/起こらないというデータです
起こる確率を計算するためグラフの形は直線ではなく、シグモイド曲線(S字型)になります。
(直線だと0を下回ったり、1を上回ってしまうから)
式 expは底をネイピア数eとした指数関数()内が指数
グラフ
ここまで、ロジスティック回帰の大まかな説明をしてきましたが
ここからは実際に使用する際の注意点を書きます。
#注意点
まずロジスティック回帰では使えない説明変数があります。
それが以下の4つです。
①優劣のない3つ以上のカテゴリーデータ（例：血液型）
②データがすべて同じ値の説明変数
③説明変数の個数が「個体数－1」より多い変数
④数値以外のデータがある個体（基本的には数値データだが、記号や空白が含まれているデータ）
ちなみに説明変数の数として、(少ない方の事象のデータ数÷10)までが投入できる数だと考えられています。
もう一つの注意点として、ロジスティック回帰は線形分離可能な分類問題に向いています。
線形分離可能とは簡単に言うと、データ空間に対し直線でうまく分類できることを言います。
2つの変数(x1,x2)があったときにx1とx2がともに高いときのみ
クラス1に分類されるというのであれば線形分離可能です
しかし、x1とx2がともに高いとき x1とx2がともに低いときのそれぞれでクラス1に分類されるときは、線形分離可能でなく、分類が難しくなることが予想されます。
そのような問題には、非線形分類に適している決定木などの手法を試すのがいいかと思います。
次は実際に動かしてみたいと思います