Edge Slideを作る【モデリングツール】

Houdini Advent Calendar 2022 7日目の記事です。

ある日、こんな質問をもらいました。
「BlenderやMayaのEdge SlideみたいなことをHoudiniでしたいんだけど、何か方法ある？」
「パラメータは 0.0 ～ 1.0 の値で調整したい」

この記事は上記の問題を解決すべく立ち上がった、
一人のエフェクトアーティストの記録です。

実際の私の思考の流れに沿って解説しますので、
皆さんも一緒に考えながら読んでみてください。

対象者

• SOPへの理解を深めたい人
• ネットワーク構築力を鍛えたい人

目標

• BlenderのEdge Slideみたいな機能を実現する

案1. Rayノードを使う（失敗）

Ray
1番目の入力ジオメトリの各ポイントをそのポイントの法線方向で、
光線を2番目の入力ジオメトリに投影させて、それらのポイントを動かします。
https://www.sidefx.com/ja/docs/houdini/nodes/sop/ray.html

最初に思い浮かんだのは、Rayノードを使う方法です。
どれだけポイントを動かしても必ずサーフェスに貼りつくので、
うまくいくと思って、試してみた結果がこちらです。

ノードネットワーク（表示する場合はクリックして下さい）

想定していた挙動とは大きく違っていて、ジオメトリも破綻しています。
オプションも見直してみましたが、理想に近づくことはありませんでした。

問題点：移動方向や距離を個別に制御できない

Rayノードはあくまで投影先にポイントを沿わせるノードであり、
各エッジの理想的な移動を担保してくれません。

案2. Edit Sopを使う

Edit（Slide on Surface）
既存サーフェスのポイントやエッジを動かす時に、
そのサーフェス上を“滑る”ようにその編集を拘束をします。
https://www.sidefx.com/ja/docs/houdini/nodes/sop/edit.html

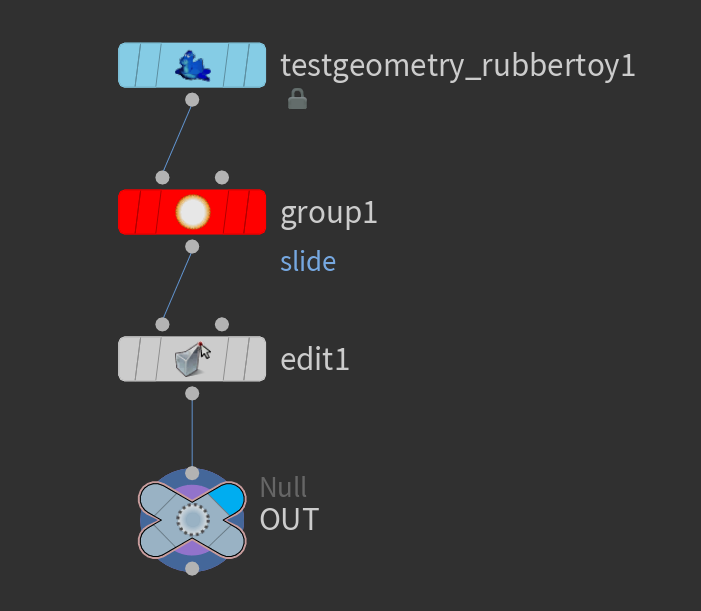
次は「Houdini Edge Slide」などの検索をしていた時に見つけたEditノードを使う方法です。
Slide on Surfaceにチェックを入れると、いい感じにエッジが移動してくれそうだったので
試してみました。

ノードネットワーク（表示する場合はクリックして下さい）

上手くいきました。「少しモデリングで使いたい」ぐらいの用途であれば
この方法で十分ですが、問題点もあります。

問題点：0.0～1.0でエッジの移動をコントロールできない

プリミティブのサイズによって、移動に必要なTranslateの値が大きく変わることや、
「0.0～1.0でコントロールしたい」という要望もあるので、Editノードでは不十分です。

案3. 自分で作る

既存のノードでは上手くいかず、HDAも見つからなかったので（※）、
自分で作ることにしました。

※ 有志の方が作られたotlはありましたが、一部不具合もあり、
　 長期間更新されていないことから、本記事では取り上げません。

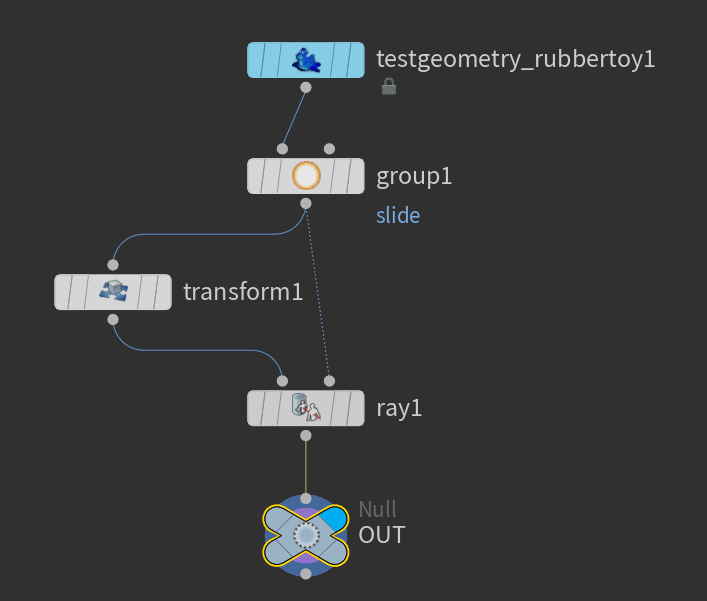
完成したネットワークはこちらです。
詳しい説明は後ほどします。

解説1. 仕組みをイメージする

Edge Slideを作るにあたって、どういう仕組みにするのかをイメージします。
私は選択したエッジAと交差するエッジBを見つけて、エッジBに沿って
エッジAを構成するポイントA'をスライドさせることを考えました。

この仕組みを実現するために必要な要素は二つです

• 交差するエッジBを見つける
• エッジBに沿ってポイントA'をスライドさせる

イメージが掴めたので、実装に取り掛かります。

解説2. テスト用モデルとエッジグループを用意する

まずは動作を確認する為のモデルを用意しましょう。
モデルの形状や選択するエッジは何でも構いませんが、あまり単純すぎると
不具合を見逃したりするので注意して下さい。
Group Nameはslide、 Group TypeはEdgesを選び、いくつかのエッジを選択します。

解説3. 選択したエッジAと交差するエッジBを見つける

エッジAと交差するエッジBはGroup Expand Sopと
Group Combine Sopを使えば探し出せます。

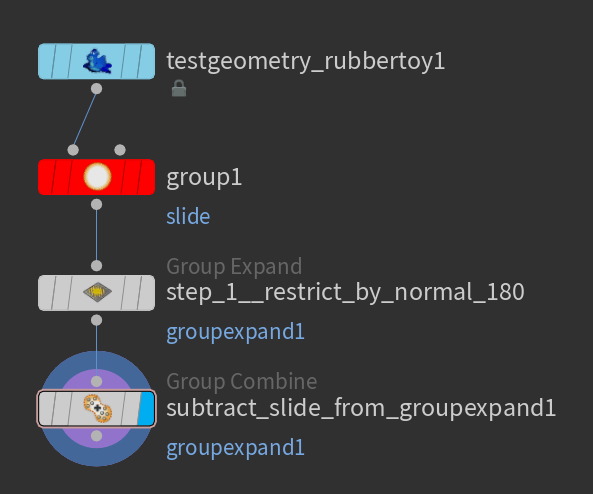
Group Expand Sopでエッジグループの範囲を広げ、
Group Combine Sopで広がったグループから元のグループを引く

これだけです。

パラメータの詳細

■ Group Expand Sop
　・Group Name：groupexpand1
　・Base Group：slide
　・Group Type：Edges
　▼ Normal Constraints
　　・Restrict by Nomarl Spread Angle：180

■ Group Combine
　・Group Name：groupexpand1
　　Equals, groupexpand1
　　Subtraction, With, slide

ここまでのノードネットワーク（表示する場合はクリックして下さい）

解説4. エッジBに沿ってポイントA'をスライドさせる

まずは、Labs Edge Group To Curve Sopを使います。

Groupをgroupexpand1にすると、エッジBだけが抽出できます。

次はポイントA'をエッジBに沿ってスライドさせるために、
Attribute Wrangle Sopを作り、↓の様に繋ぎます。

繋いだ後は、Attribute Wrangle Sopにコードを書いていくのですが、
その際に、VEX関数のxyzdist(), primuv()を使います。

xyzdist()のイメージ
Rayノードを使って、ポイントをジオメトリにくっ付けた後、
くっ付いた場所がジオメトリのUV空間のどの位置（uv）にあるのかを調べる。
（距離やプリミティブ番号も調べられます）

primuv()のイメージ
ジオメトリ上で指定したUV座標の位置がワールド空間のどこ（P）にあるのかを調べる。
（@P以外のアトリビュートも調べられます）

xyzdist()でポイントA'に一番近いエッジBの位置座標を、UV座標として取得した後、
取得したUV座標をずらし、primuv()を使ってUV座標を位置座標に変換して@Pに代入すると、
ポイントA'をエッジBに沿ってスライドさせることが出来るようになります。

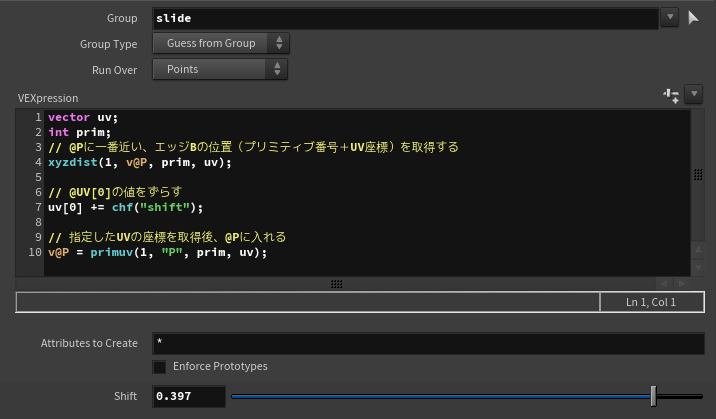
しかし、まだ問題があります。
ポイントA'のスライドする方向がバラバラになってしまう事です。

原因は、それぞれのエッジBに対して UV[0] が 0.0 のときの位置座標が違っているからです。

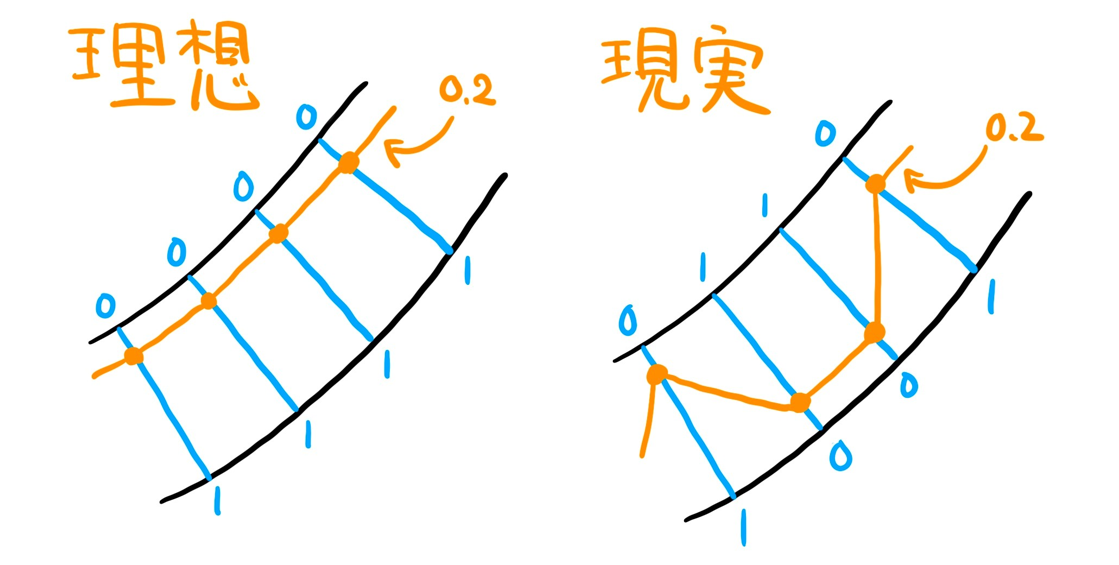
パラメータの詳細

■ Attribute Wrangle Sop
　・Group ：slide

Attribute Wrangle

vector uv;
int prim;
// @Pに一番近い、エッジBの位置（プリミティブ番号＋UV座標）を取得する
xyzdist(1, v@P, prim, uv);

// @UV[0]の値をずらす
uv[0] += chf("shift");

// 指定したUVの座標を取得後、@Pに入れる
v@P = primuv(1, "P", prim, uv);

解説5. 問題点を洗い出す

先ほど、「UV[0] が 0.0 のときの位置座標が違っている」と書きましたが、
UVを貼り直して位置座標を合わせれば良いだけだと考えるかもしれません。

しかし、その解決方法には2つの乗り越えなければならない問題があります。

• 位置座標を合わせる基準が存在しない
• UVを編集できない

位置座標を合わせる基準が存在しない

UVの向きを全て揃えるには、エッジの始点となるポイントを決める必要があります。
「Y座標が一番高いポイントを始点にしよう」などと考えるかもしれませんが、
エッジの角度は様々ですし、単純なソートで得られる値をそのまま基準には出来ません。
ベクトルの内積・外積を使って基準を作り出す必要があります。

UVを編集できない

xyzdist()で取得できるUVはintrinsic primitive UVsと呼ばれるものです。
様々なVEX関数を使って値を取り出すことは出来るのですが、編集は出来ませんでした。
つまり、理想的なUVを持つプリミティブを再生成する必要があります。
今回、作り直しの対象であるエッジは既にLabs Edge Group To Curve Sopで抽出
されていますので、Add Sopを使ってもう一度エッジを生成し直すだけで済みます。

問題が把握できたところで、ネットワークの構築に進みます。

解説6. プリミティブを再生成する

基準を作る前に、プリミティブを再生成するためのネットワークを組んでしまいます。

まずはAttribute Create Sopを作り、↓の場所に繋ぎます

Nameはid, TypeはInteger, Valueは@ptnumとします。
@idはアトリビュートをコピーしたり、ポイントをソートするのに使います。

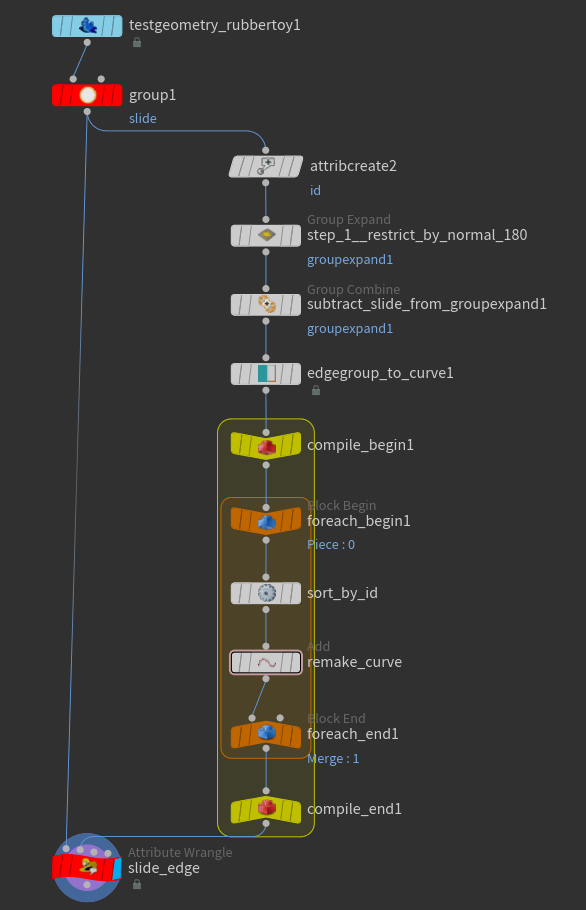
次はSort SopとAdd Sopを作り、
For-EachブロックとCompileブロックで囲います。

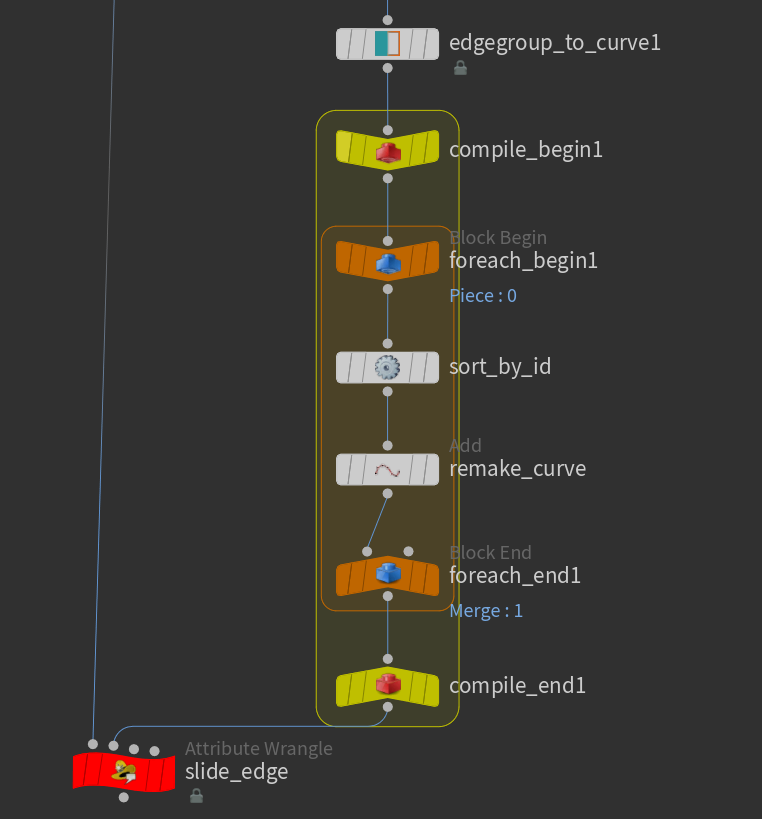
For-Eachブロックを作るときは、For-Each Primitiveを選びます。
また、Compileブロックで囲った後は、For-EachブロックのBlock End Sopで
Multithread when CompiledのチェックをONにすることを忘れないでください。

これでエッジを再生成することが出来るようになりました。
Add Sopではポイント番号の順にエッジを生成していますので、
その前に、ソート基準を作り（@id）それに従ってポイント番号をソートする
必要があります（方法は後述します）。

その他のパラメータの値については↓のパラメータの詳細にて記載していますので、
そちらを参照ください。

パラメータの詳細

■ Attribute Create Sop
　・Name ：id
　・Type ：Integet
　・Value ：@ptnum, 0, 0, 0

■ Sort Sop
　・Point Sort ：By Attribute

■ Add Sop
　・Delete Geometry But Keep the Points ：チェックON

■ For-Eachブロック
　・タブメニュー ：For-Each Primitive
　・Multithread when Compiled ：チェックON

ここまでのノードネットワーク（表示する場合はクリックして下さい）

解説7. ソート基準を作る

これからソート基準を作るのですが、その前に知っておかなければならない
ベクトルの内積と外積について簡単に解説します。

ベクトルの内積

ベクトルAとベクトルBがどのぐらい似ているのかを-1.0～1.0の値で示します。
dot(ベクトルA, ベクトルB)と書くと計算されます。
（↑の式の場合、ベクトルBがベクトルAにどれだけ似ているかが分かります）

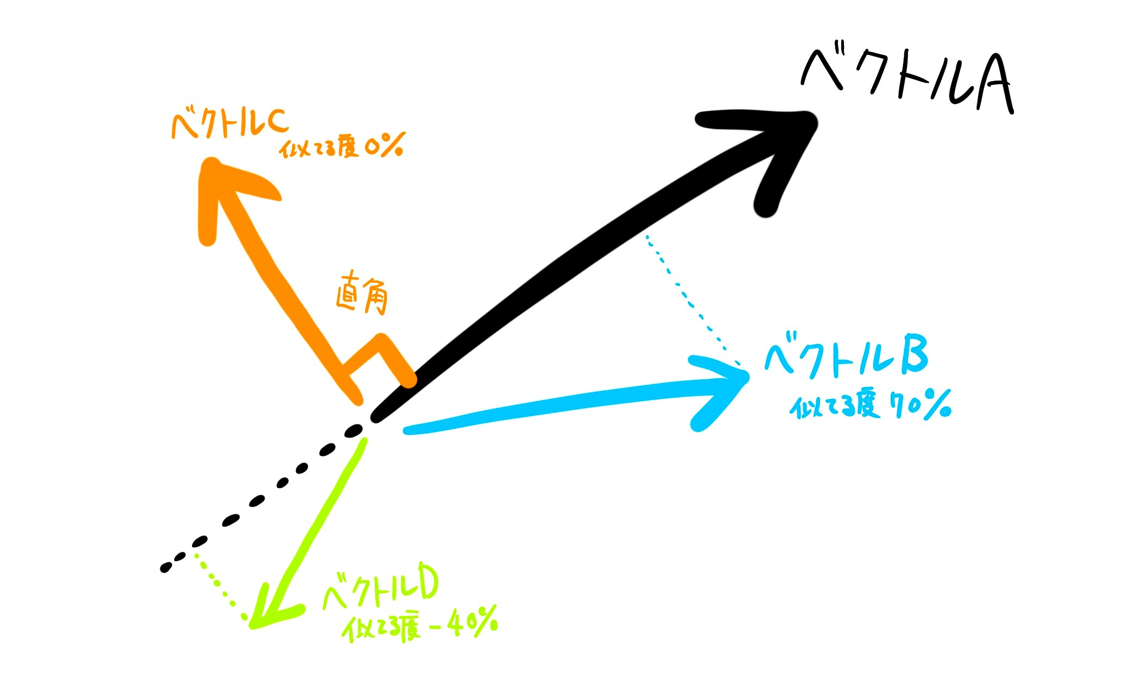
ベクトルの外積

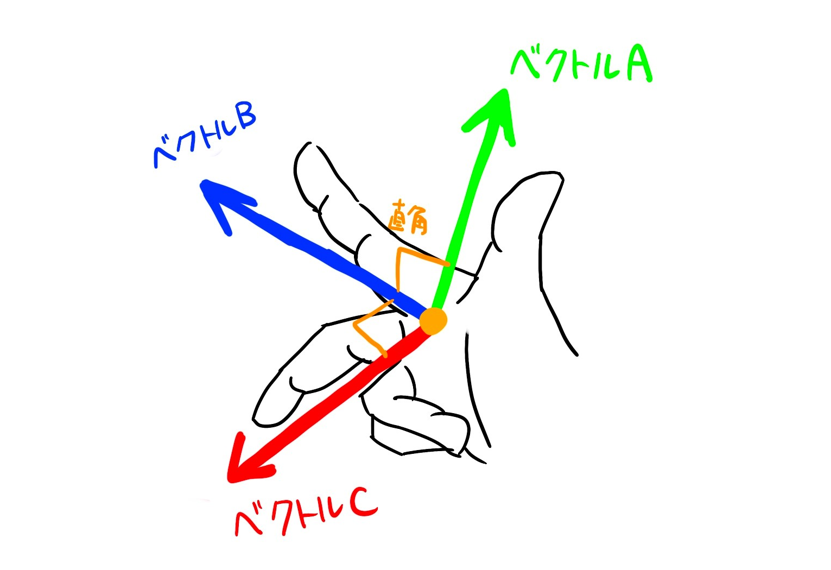
ベクトルAとベクトルBに対して直角なベクトルCを示します。
cros(ベクトルA, ベクトルB)と書くと計算されます。
ベクトルCの向きはベクトルを掛けた順番によって変わるので注意してください。
（↓のように中指= cross(親指, 人差し指)と覚えると楽です。）

ベクトルの内積・外積が理解できたところで、ソートを作る方法を解説します。
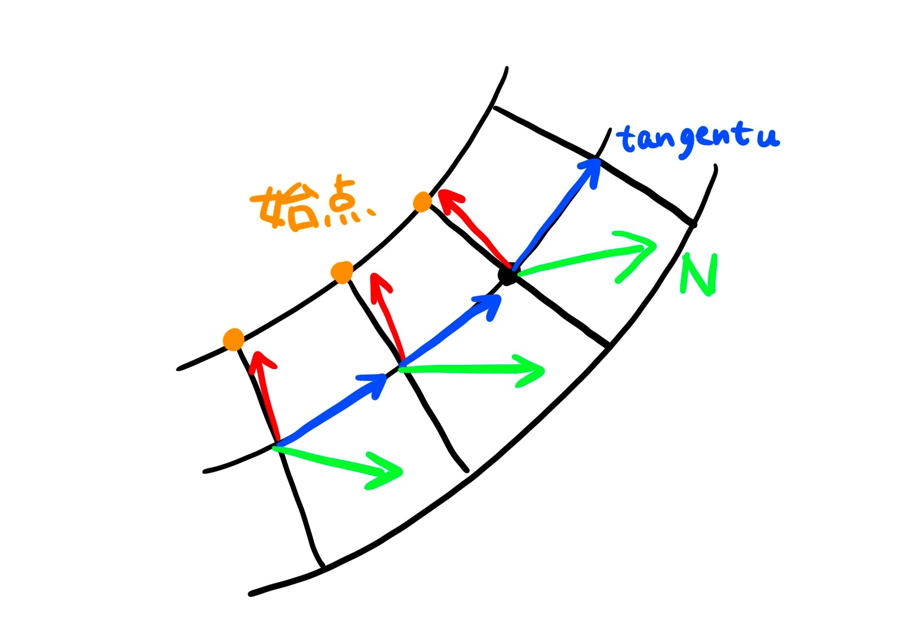
それは「オブジェクトの法線(@N)と接線(@tangentu)を外積して出来たベクトルCと
同じ方向にあるポイントを始点にする」です。

目標が決まったのでネットワークを構築していきます。
まずは、Normal Sopを作り、ポイントに法線情報を持たせます。
その後、Labs Edge Group To Curve SopとPolyFrame Sop、
Attribute Create Sop、Attribute Copy Sopを作り、↓のように接続します。

Labs Edge Group To Curve Sopで選択エッジのみを抽出し、
PolyFrame Sopでエッジの接線（@tangentu）を計算しています。

Attribute Create Sopでは選択エッジが中心であることを示すための
centerアトリビュートを作り、Attribute Copy Sopで@tangentu,
@centerを元のジオメトリにコピーしています。

次はAttribute Wrangle SopとAttribute Create Sopを作ります。

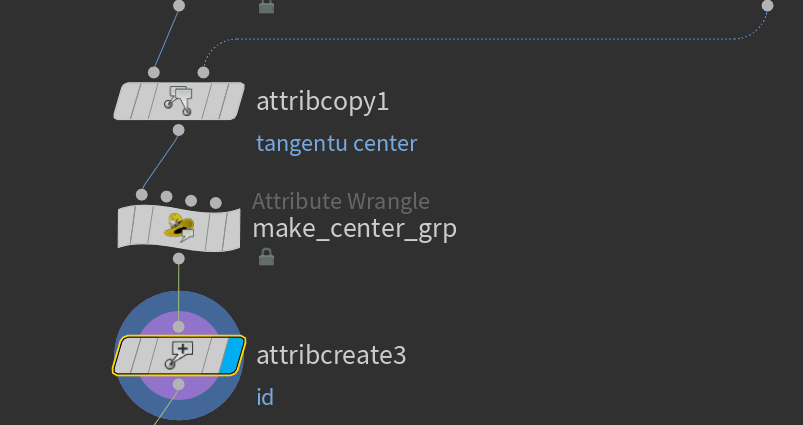
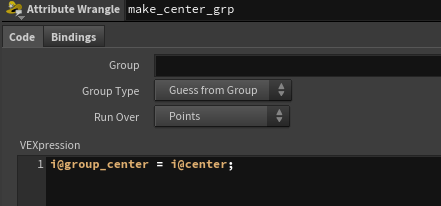
Attribute Wrangle Sopではcenterアトリビュートをグループ情報に変換しています。
（グループはVEXで@group_グループ名 = 1と書いても作れます）

Attribute Create Sopは既にあるidアトリビュートを全て1で上書きしています。

全てのアトリビュートの準備が整いましたので、ソート基準を作成します。
Attribute Wrangle Sopを作り、↓のように繋ぎます。

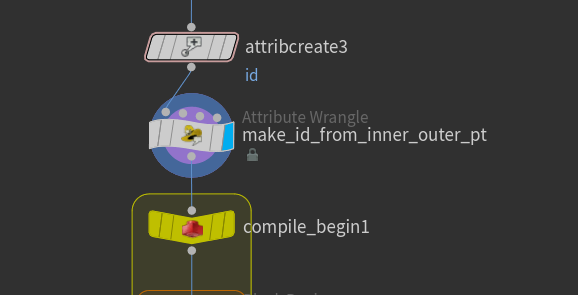
Attribute Wrangle Sopの中では、始点と終点を求めるコードを書いています。
（@idの値が始点：0, 中間：1, 終点：2になるようにしています）

これで理想的なポイントのソートが出来るようになり、
エッジのスライド方向も統一されました。

パラメータの詳細

■ Normal Sop
　・Add Normals to ：points

■ Labs Edge Group To Curve Sop
　・Group ：slide

■ PolyFrame Sop
　・Normal Name ：チェックOFF

■ Attribute Create Sop (attribcreate1)
　・Name ：center
　・Type ：Integer
　・Value ：1,0,0,0

■ Attribute Copy Sop
　・Match by Attribute ：チェックON
　・Attribute to Match ：id
　・Attribute Name ：tangentu center

■ Attribute Wrangle Sop（make_center_grp）

Attribute Wrangle

i@group_center = i@center;

■ Attribute Create Sop（attribcreate3）
　・id ：id
　・Type ：Integer
　・Value ：1,0,0,0

■ Attribute Wrangle Sop（make_id_from_inner_outer_pt）
　・Group ：!center

Attribute Wrangle

// center以外の全てのポイントで実行される

//　自身から一番近いcenterのポイント番号を取得
int center_pt = neighbour(0, @ptnum, 0);

// centerに格納されている各アトリビュートを取得
vector center_pos = point(0, "P", center_pt);
vector center_nml = point(0, "N", center_pt);
vector center_tnj = point(0, "tangentu", center_pt);

// centerから自分（ポイント）に向かうベクトルを作る
vector tnj = normalize(@P - center_pos);

// centerの法線と接戦の外積から始点方向を指すベクトルを作る
// 自分に向かうベクトルと始点方向を指すベクトルの内積を取る
if(dot(tnj, cross(center_nml, center_tnj)) > 0)
{
    // 内積の結果が0より大きい場合、自分（ポイント）は始点である
    @id = 0;
}
else
{
    // 内積の結果が0より小さい場合、自分（ポイント）は終点である
    @id = 2;
}

解説8. 完成

全体のノードネットワーク（表示する場合はクリックして下さい）

おわり

如何だったでしょうか。
かなり雑な実装になってしまいましたが、速度も求めてませんし、
個人的にはこのぐらいでいいかなと思っています。

もし最適化する場合は、全部をコードに書き直す必要がありますので
興味のある方は挑戦してみてください！

ここまで読んでいただきありがとうございました！