【Python】備忘録 正規分布の面積を求める自作関数

備忘録

統計学に関する初歩的な関数
N(0,1^2)に従う正規分布のグラフの面積を求めるだけ。

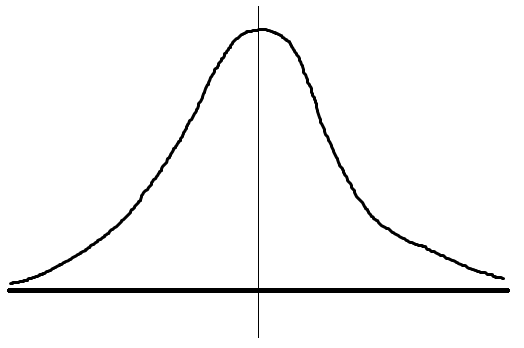
↑これ
このポリープみたいな曲線の式は、
$$ f_{(x)}=\frac{1}{\sqrt{2x}}e^{(-\frac{x}{2})} $$
で与えられます。
コメントしてくれた人、有難うございます。

ソース(誰得)

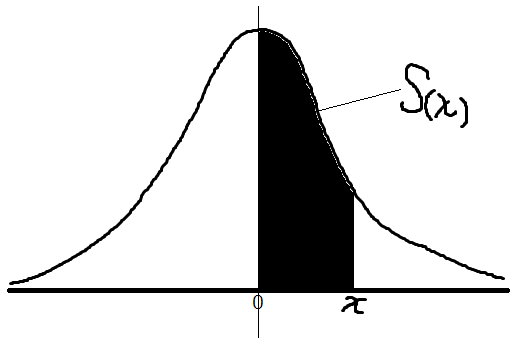
1. 0からxまでの面積を求める

NORMAL_Dist_S

def NORMAL_Dist_S(a):
    """N(0,1^2)に従う正規分布の x=0からaまでの面積を返す"""
    import numpy as np
    import math
    from scipy import integrate


    f = lambda x: (math.exp(-x**2/2)) / math.sqrt(2*math.pi)
    s,d = integrate.quad(f, 0, abs(a))
    return s

NORMAL_Dist_Sは、

x=任意の実数
res = NORMAL_Dist_S(x)
と書き、

S(x)の値をresに返します。

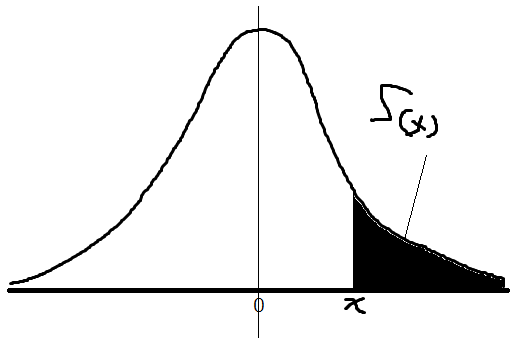
2. x=∞からxまでの面積を求める

NORMAL_Dist_S_REST

def NORMAL_Dist_S_REST(a):
    """N(0,1^2)に従う正規分布の x=0からaまでの面積を0.5から引いた値を返す"""
    import numpy as np
    import math
    from scipy import integrate


    f = lambda x: (math.exp(-x**2/2)) / math.sqrt(2*math.pi)
    s,d = integrate.quad(f, 0, abs(a))
    s=0.5-s
    return s

NORMAL_Dist_S_RESTは、

x=任意の実数
res = NORMAL_Dist_S_REST(x)
と書き、
S(x)の値をresに返します。

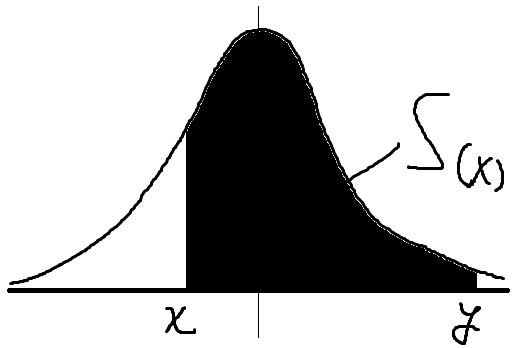
3. 任意の2地点の積分

NORMAL_Dist

def NORMAL_Dist(a,b):
    """N(0,1^2)に従う正規分布の aからbまでの面積を返す"""
    import numpy as np
    import math
    from scipy import integrate


    f = lambda x: (math.exp(-x**2/2)) / math.sqrt(2*math.pi)
    s,d = integrate.quad(f, a,b)
    return s

NORMAL_Distは、

x=任意の実数
y=任意の実数
res = NORMAL_Dist(x,y)
と書き、
S(x)の値をresに返します。

感想

もっと単純明快かつ高速にかけそう
故に、誰得関数。

どんどん関数を増やしていきたい。(誰得なのに!!??)
なんだかんだいって、自分は使う場面が結構あるし、
めんどくさいからこの機会に思い切って関数化。

てかこの程度なら、pythonのimportするライブラリになんかあると思う。
というより、ないはずがない。

出典など

http://org-technology.com/posts/integrate-function.html
https://ja.wikipedia.org/wiki/%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83