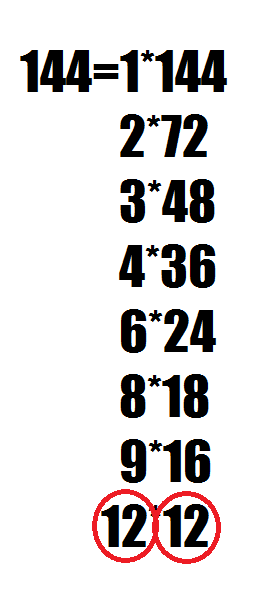1.素数とウラムの螺旋
そもそも、ウラムの螺旋とは?
ウラムの螺旋とは、中心を1として、反時計回りに2,3,4,5,6,7・・・・と
数字の点を螺旋状に描き、素数のところだけを残していくと出来る図形のことである。
詳しくはWikipediaで見ればわかるんですけど、
素数に規則性みたいなのが浮かび上がってくるという不思議な図形です。
コピペだけでこいつが楽しめます。
ちなみに画像のサイズは、画面のタテの画素数に依存します。
ちなみに、FullHDで実行した結果は、
1-1164241(1079^2)までの数字の素数を判断し、
素数は90359個存在し、
9343個の双子素数(ただし、2,3は双子素数とはみなさない)が存在し、
最大の素数は1164221です。
2.素数の判断と高速化
素数に規則性があれば、もはやこのような螺旋を描いて楽しむようなことはできませんが、できるだけ早く素数と判断できればいいですよね?
2-1.ふるいにかけるという方法
「エラトステネスのふるい」
「アトキンのふるい」
「サンダラムのふるい」
という3つのふるいがあるようだ。
素数でないものを削ぎ落とすという方法。
・良い点
速い。
複雑な計算ではない。
(アトキンのふるいは例外のようだが、
サンダラムのふるいはWikipediaにGIFが載っているが
一目瞭然。 すごく簡単なふるいである。)
・良くない点
配列を用意するのでリソースを大量に消費する。
数字に限度がある。(int型の限界よりもずっと小さい)
↑メモリの関係ですね これは
2-2. 実際に割って確かめる
愚直に数を2から割っていく方法。
素数の定義通りにやっていく原始的なやり方。
高速化のために、偶数で割らないとか偶数の数字は無視するとか・・・
すぐに思いつく。
・良い点
ソースがとても簡単(10行もかからずに実装可能)
・良くない点
素数かどうかを求める数が大きくなると
計算速度がうなぎのぼりに増える。
(y=xにそぐう形で増える)
2-2改. 平方数を使う
2-2の発展版。
理系の人は知ってて「当たり前」思いますが
求める数の正の平方根+1まで割り切れなければその数は素数
例えば、144だと約数は以下のとおり
√144 = 12。
12がちょうど折り返し地点となっているため
素数かどうかを確認するためには、
正の平方根のところまで調べれば良い。
ただ、すべての数の正の平方根が自然数で表せるわけでもないので、
[√素数かどうか知りたい数]+1 まで調べれば良い。
(正式な証明ではありませんが まぁこんな感じ。)
実際この下のソースでもこの方法を使っております。
else if(know%2==1){
for(long h=2; h<=sq; h++){
amari=know%h;
if(amari==0){//warikire
return;
}
else if(know>5 && know%5==0){
return;
}
else{
if(h==sq){
point(zahyox,zahyoy);
}
最初のfor文で[平方根]+1までループさせる。
if文で 偶数を無視。
else ifで わかりやすい5の倍数を無視。
最後までループが続けば、素数であるといった形です。
3.ソース
long cx,cy; //center position
long sq_dk; //square dekasa
long pax,pay; //palong x palong y
long sq_kx,sq_ky; //square kaisi x y (x,y)= (2n+1)^2
long dipx,dipy;//display x display y
long cnt=1; //sosu;
long pv;
long bpm=2;
long npm=2; //before pm after prime
long twn; //twin prime number;
long mxp=1; //MAX prime
void setup(){
background(0);
noLoop();
noFill();
size(displayHeight,displayHeight);
dipx=displayWidth;
dipy=displayHeight;
if(dipx > dipy){
cx=((long) (dipy/2));
cy=cx;
sq_dk=((long) (dipy/2))-1;
}
else if(dipx <= dipy){
cy=((long) (dipx/2));
cx=cy;
sq_dk=((long) (dipx/2))-1;
}
pv=1;
}
void draw(){
background(0);
stroke(#FFFFFF);
uramu();
}
void uramu(){
for(long i=1; i<=sq_dk; i++){
sq_kx=cx+i;
sq_ky=cy+i;
pax=sq_kx;
pay=sq_ky;
for(long j=0; j<2*i; j++){
cnt++;
pay--;
isprime(cnt,pax,pay);
}
for(long k=0; k<2*i; k++){
cnt++;
pax--;
isprime(cnt,pax,pay);
}
for(long l=0; l<2*i; l++){
cnt++;
pay++;
isprime(cnt,pax,pay);
}
for(long m=0; m<2*i; m++){
cnt++;
pax++;
isprime(cnt,pax,pay);
}
}
}
void isprime(long a, long x,long y){
long know=a;
long sq=((long)(Math.sqrt(a)))+1;
long amari=0;
long zahyox=x;
long zahyoy=y;
if(know%2==0){
//nani mo sinai.
amari=know%2;
if(know==2){
point(zahyox,zahyoy);
}
return;
}
else if(know%2==1){
for(long h=2; h<=sq; h++){
amari=know%h;
if(amari==0){//warikire
return;
}
else if(know>5 && know%5==0){
return;
}
else{
if(h==sq){
point(zahyox,zahyoy);
}
}
}
}
}
4.おまけ
long cx,cy; //center position
long sq_dk; //square dekasa
long pax,pay; //palong x palong y
long sq_kx,sq_ky; //square kaisi x y (x,y)= (2n+1)^2
long dipx,dipy;//display x display y
long cnt=1; //sosu;
long pv;
long bpm=2;
long npm=2; //before pm after prime
long twn; //twin prime number;
long mxp=1; //MAX prime
void setup(){
background(0);
frameRate(-1);
size(displayWidth,displayHeight);
noFill();
dipx=displayWidth;
dipy=displayHeight;
if(dipx > dipy){
cx=((long) (dipy/2));
cy=cx;
sq_dk=((long) (dipy/2))-1;
}
else if(dipx <= dipy){
cy=((long) (dipx/2));
cx=cy;
sq_dk=((long) (dipx/2))-1;
}
pv=1;
}
void draw(){
background(0);
stroke(#FFFFFF);
uramu();
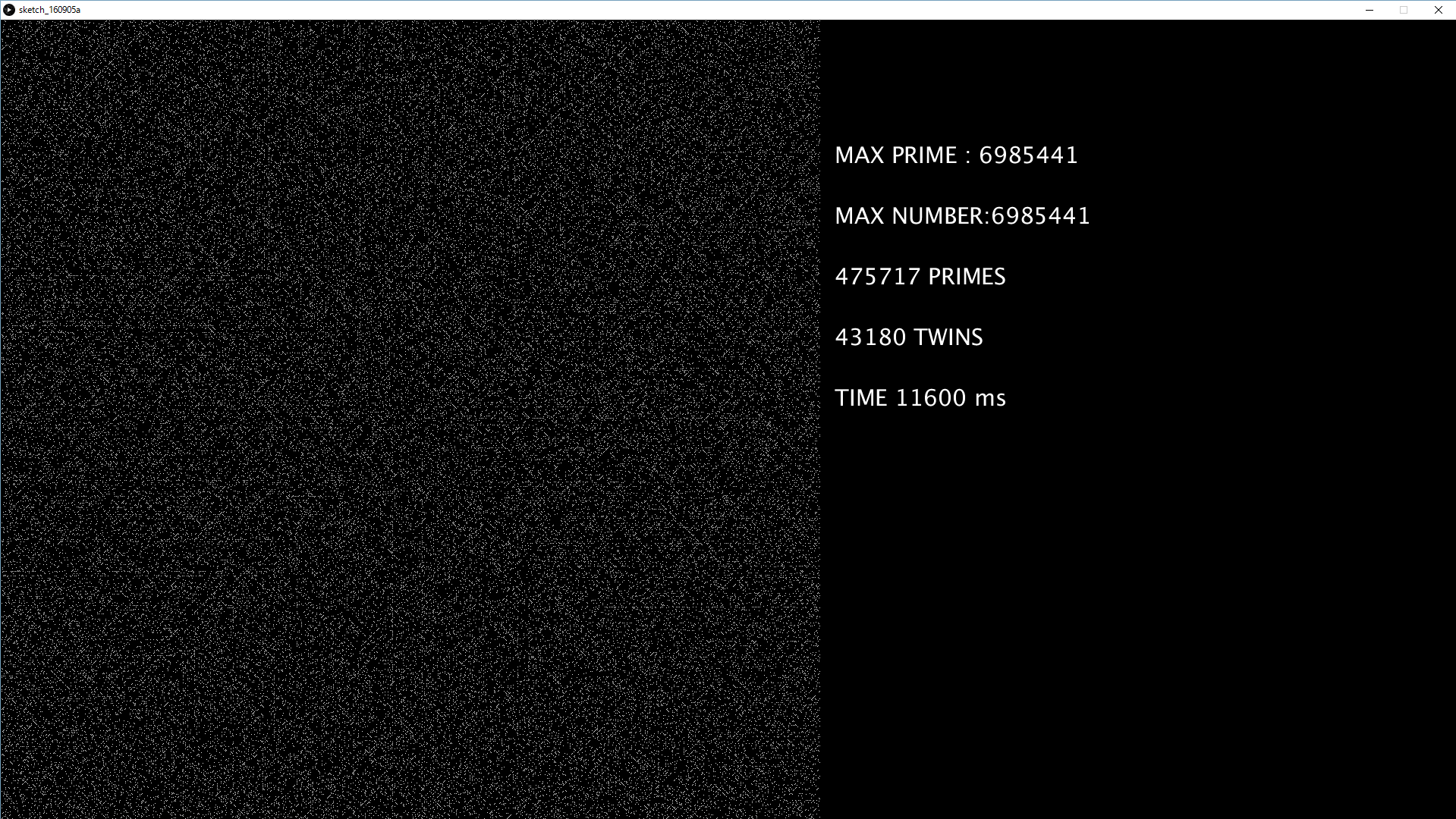
textSize(30);
//text("FPS "+frameRate, sq_dk*2+1+20, 80,400,100);
text("MAX PRIME : "+mxp, sq_dk*2+1+20, 160 ,400,100);
text("MAX NUMBER:"+cnt, sq_dk*2+1+20, 240 ,400,100);
text(pv+" PRIMES", sq_dk*2+1+20, 320 ,400,100);
text(twn+" TWINS", sq_dk*2+1+20, 400 ,400,100);
text("TIME "+millis()+" ms",sq_dk*2+1+20, 480 ,600,100);
//cnt=1;
//pv=1;
//twn=0;
}
void uramu(){
//polong(cx,cy); 1
for(long i=1; i<=sq_dk; i++){
sq_kx=cx+i;
sq_ky=cy+i;
pax=sq_kx;
pay=sq_ky;
for(long j=0; j<2*i; j++){
cnt++;
pay--;
isprime(cnt,pax,pay);
}
for(long k=0; k<2*i; k++){
cnt++;
pax--;
isprime(cnt,pax,pay);
}
for(long l=0; l<2*i; l++){
cnt++;
pay++;
isprime(cnt,pax,pay);
}
for(long m=0; m<2*i; m++){
cnt++;
pax++;
isprime(cnt,pax,pay);
}
}
}
void isprime(long a, long x,long y){
long know=a;
long sq=((long)(Math.sqrt(a)))+1;
long amari=0;
long zahyox=x;
long zahyoy=y;
if(know%2==0){
//nani mo sinai.
amari=know%2;
if(know==2){
point(zahyox,zahyoy);
}
return;
}
else if(know%2==1){
for(long h=2; h<=sq; h++){
amari=know%h;
if(amari==0){//warikire
return;
}
else if(know>5 && know%5==0){
return;
}
else{
if(h==sq){
point(zahyox,zahyoy);
//
bpm=npm;
npm=know;
if(Math.abs(npm-bpm)==2){
twn++;
}
pv++;
//
}
else{
}
}
}
}
//
if(a>mxp){
mxp=a;
}
//
}
スクリーンセーバーもどき
出典
https://ja.wikipedia.org/wiki/%E3%82%A6%E3%83%A9%E3%83%A0%E3%81%AE%E8%9E%BA%E6%97%8B
↑ Wikipedia ウラムの螺旋 ↑
素数関係
http://www.higashi-h.tym.ed.jp/course/kadai15/matome/sosu.htm
↑素数のいろいろ↑