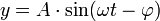音のデジタル表現を理解する
今回は、物資の振動という、とてもアナログなものであるところの「音」というものが、デジタル信号の世界でどのようにして表現されるかを見ていきます。
16bit/44.1kHz とはどういう意味か?
前回の記事で例として挙げた、CD のデジタル規格である 16bit/44.1kHz とはどういう意味でしょうか?
これは、いきなり結論から言うと、CD のフォーマットが、
- ビット深度(量子化ビット数): 16bit
- サンプリングレート: 44.1KHz
であることを表しており、そのままこれは音質を示す指標とすることも可能です。
ビット深度については、開発者であれば馴染みのある方もいるかもしれません。
これはある一定の単位あたりのビット数を示しており、身近なものとしては、パソコンの画像などでの、1ドットあたりの色の数を示したりします。
デジタルな音の世界でのビット深度とは、時間軸上のある1単位において、波形が示す点をどれだけ細かく分解し表現できるか、を示すものです。
そして、サンプリングレートというのが、その時間軸上のある1点というものを、どれだけ細かく分解し表現できるか、を示すものです。
と、いうのが一応の定義ですが、上記の説明だけではなかなかピンとこないと思いますので、これより単純なサンプルとしてサイン波を使って視覚的に説明したいと思います。
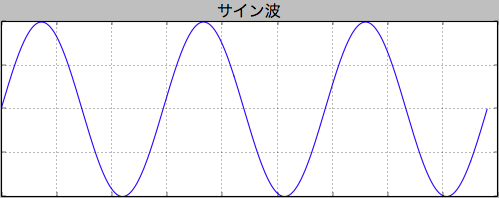
サイン波の波形
サイン波とは?
まず、解説のサンプルとして扱う「サイン波」というものを簡単に説明します。
サイン波は正弦波とも言われ、音を表すものとして最も単純な波形を持つものです。
上図が、一般的なサイン波の波形です。
横軸が時間軸で、縦軸が、後述しますが、振幅を示しています。
音の高さは周波数で表すことができるのはご存知と思いますが、この図でいうと、グラフの角度が急なほど周波数が高く、なだらかであるほど低い周波数を表します。
このサイン波というものは、最も単純な波形であり、また、音を表すものとして最も純粋なものであると言うこともできます。
ここで少々脱線しますが、自然界には、こういった純粋なサイン波の音というのは実際には存在しません。
例えば、ピアノの音を想像してみてください。
ご存知の方も多いと思いますが、ピアノで「ド」の音を鳴らしたとき、実際には「ド」の音階、これを「基音」といいますが、それ以外にも「倍音」という、基音の周波数を整数倍した音が含まれます。例えば、3倍音(ソ)、5倍音(ミ)などです。
ピアノの音とオルガンの音、同じ「ド」でも音が全然違いますよね。それは、この倍音がどのように含まれるか、によるものです。
つまり、音のキャラクターを決定するものが倍音であると言えます。
サイン波というのは、上記した「倍音」を一切含んでいない、厳密に、純粋な1つの音程を示すものです。
ちなみに、音の感じは電話が切れた時の「ツーツーツー」といった音の感じに似てます。
自然界に存在せず耳馴染みはないかもしれませんが、単純であることがサンプルとしては適切であるため、以降はこのサイン波を例として進めます。
サイン波を表す式
数学で「正弦曲線」として習った方もいると思いますが、上記したサイン波の曲線は以下の公式で示されます。
ここで、t は時刻 、A は振幅(波の中心からの最大偏差)、ω は角周波数、−φ は初期位相(t = 0 における位相)といいます。
これらのうち、初期位相というのはこれからの話にはあまり関係がないため、常に0であることに固定し、これからはサイン波の曲線は、以下の式で表していくことにします。
y = 振幅*sin(周波数*時刻)
この式により、サイン波の曲線を描くことができますが、もし、サイン波が現実に存在した場合、その振動を示す波形をそのまま表現するには無限個の点が必要になり、デジタルなグラフで表現することはできず、近似で表すことになります。
この近似は、曲線を形成する点のサンプル個数が多ければ多いほど、細かければ細かいほど実際の曲線に近いものになります。
このサンプル個数の数と細かさが、デジタルな世界での音の表現の指標として使われる、サンプリングレートとビット深度になります。
サンプリングレートとビット深度
前節で、波形を表す曲線を、デジタル表現するための忠実度が、サンプリングレートとビット深度で示されると説明しました。
より分かりやすくするため、引き続きサイン波を例として説明します。
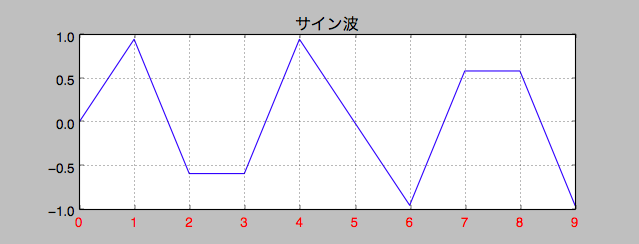
以下の曲線を見てください。
「サイン波」と堂々と書いてありますが、このガタガタのどこがサイン波なんだ!声を荒げたくなるような悲惨なものになっています。
というか、曲線ですらありません。
なんでこんな悲しいことになってしまったのでしょうか。
実はこれは、時間軸である横軸の分解精度を10にしています。ここで、横軸は全部で1秒を表している、としてください。そうするとこれは、1/10秒ごとにサイン波の式でサンプルを取得して曲線を描いたもの、と見做せます。
では、これをもっとまともな曲線にするにはどうすればよいでしょうか?
当然、サンプル精度を上げればよいわけです。
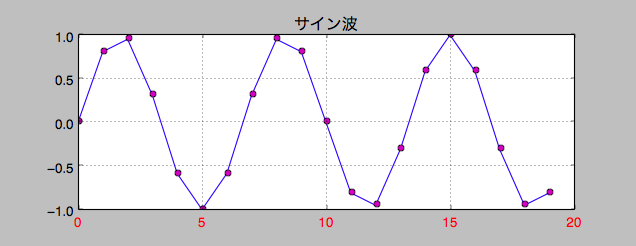
1/20秒
わかりやすいように、サンプル観測点に印をつけています。
先の1/10秒に1つのものよりは、ずいぶんと曲線に近づいてきたのが見て取れるでしょう。
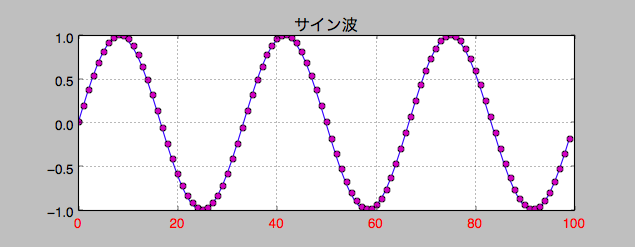
1/100秒
サンプル精度を1/100秒に1つにすると、かなり表現したい曲線を描くことができています。
このように1秒間に100回サンプリングを行うことは、言い換えると、 サンプリングレート 100Hz と表すことができます。
つまり、CD のサンプリングレート 44.1KHz というのは、1 秒間に 44100 回の精度でサンプリングを行うということです。
ここまで例としてみてきたのは横軸(時間軸)の精度ですが、同様のことが縦軸(振幅)にも言えます。
あるサンプリング周期の観測地点において、どれほど縦軸の振幅を細かく表せるか、によって曲線の再現度が決まります。
こちらは開発者の方はすぐにわかりますよね。
CD のビット深度 16bit というのは、サンプリング周期に 2 の 16 乗、つまり 65,536 の分解精度で振幅の表現ができるということです。
次回に向けて
ここまで、デジタル信号の世界での波形の表し方を見てきました。
CD の音質でサイン波を表現する場合、1秒間に44100回、16bit精度の値で曲線を描けばよい、ということが分かりました。
もしかしたら、もうすでにプログラマーの方はピンと来ているのではないでしょうか。
ということは、CD音質の1秒間の音は、44100個の要素を持つ16bit float型の配列で表現できる!!
いやあ、もりあがってきましたね!
次回は、サイン波を実際にプログラムで書きます。
おまけ
本稿で載せたグラフは全て、以下のPython用ライブラリを利用して作っています。
手軽で便利です。
- numpy (数値計算ライブラリ)
- matplotlib (グラフ描画ライブラリ)