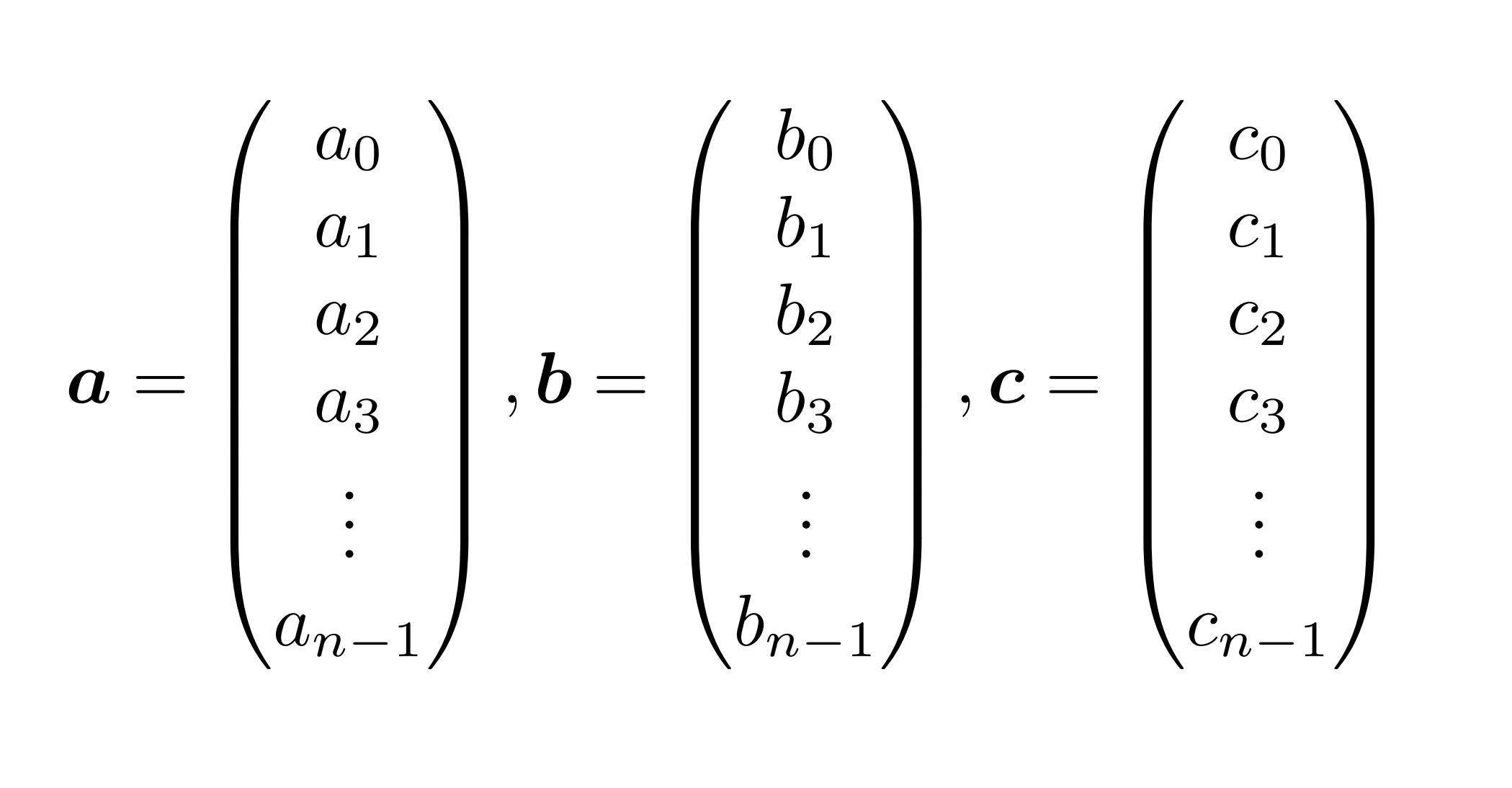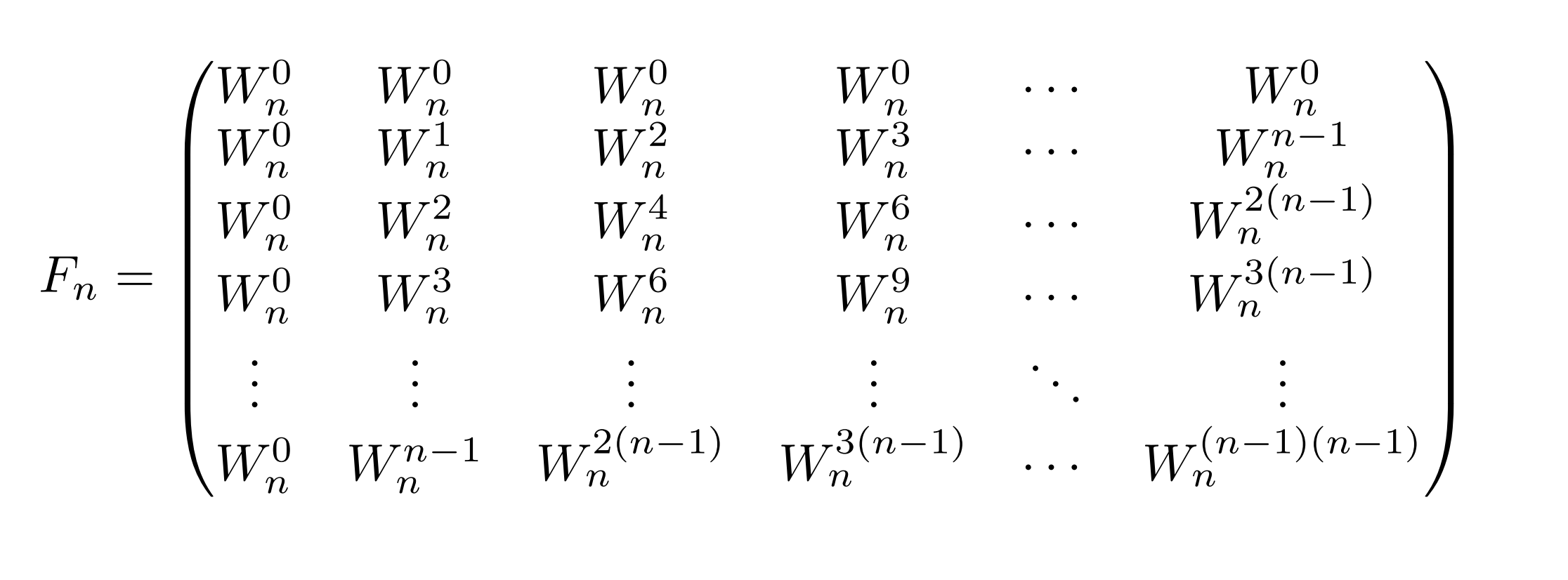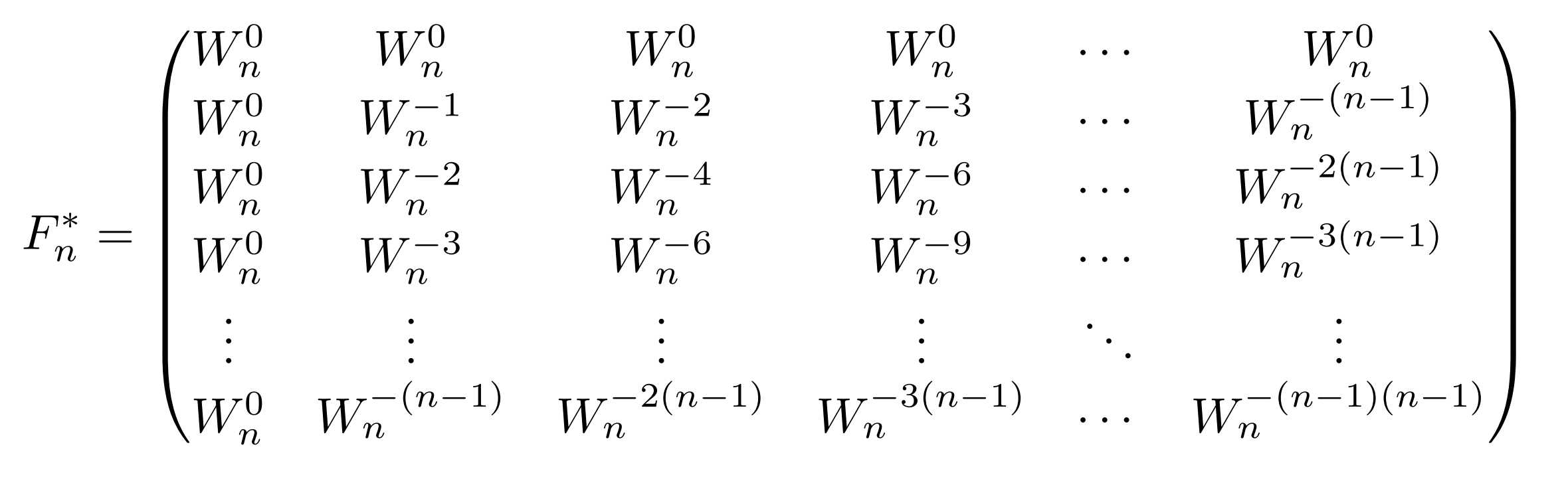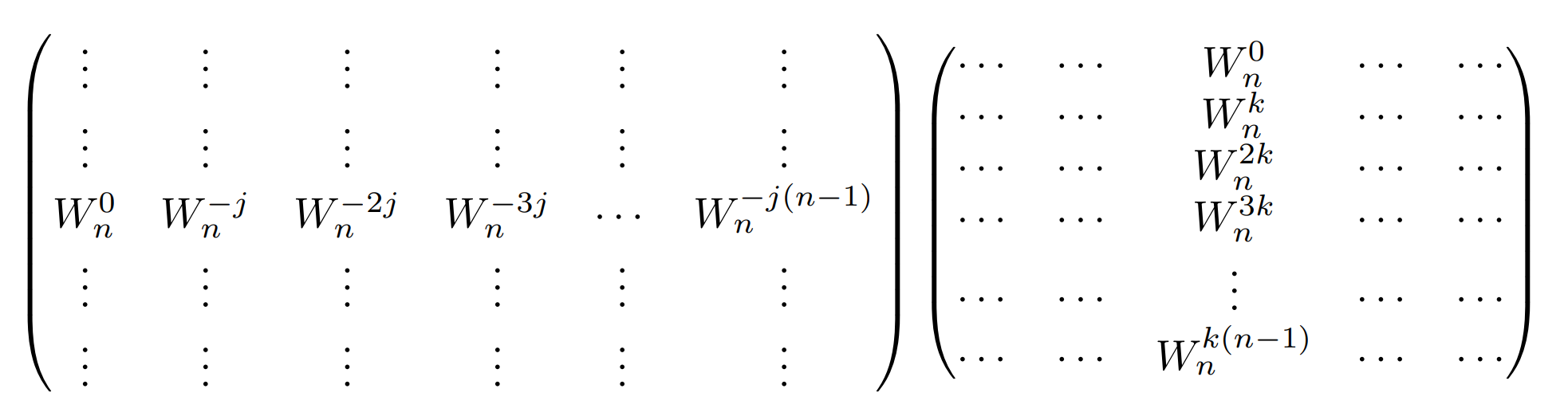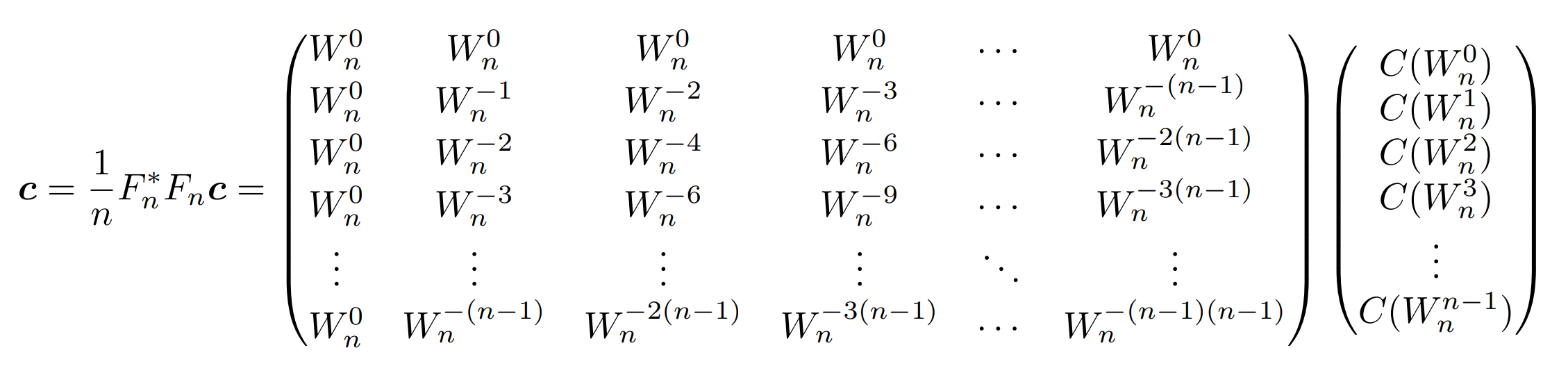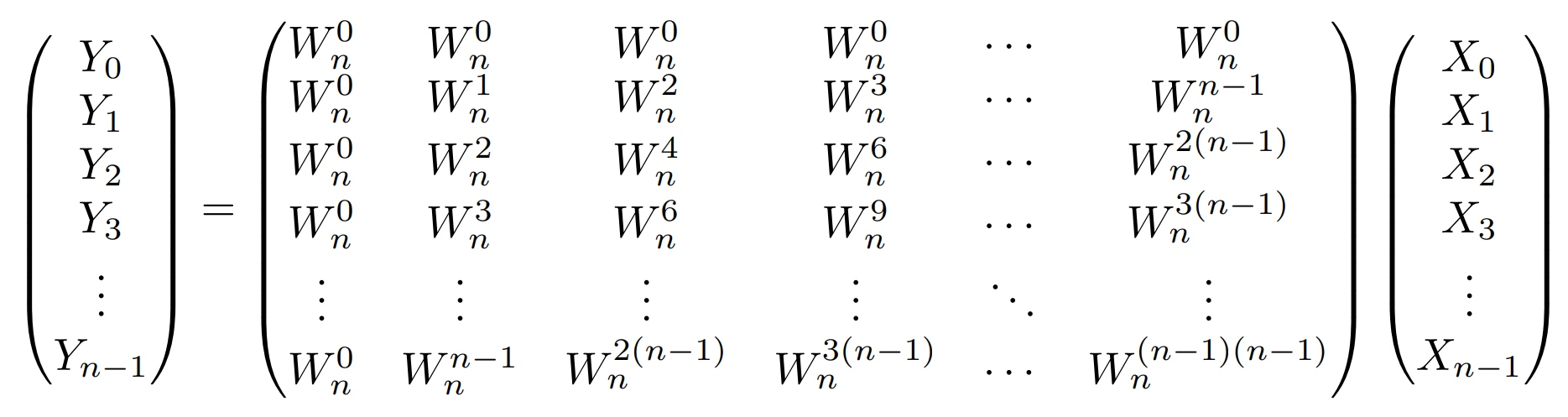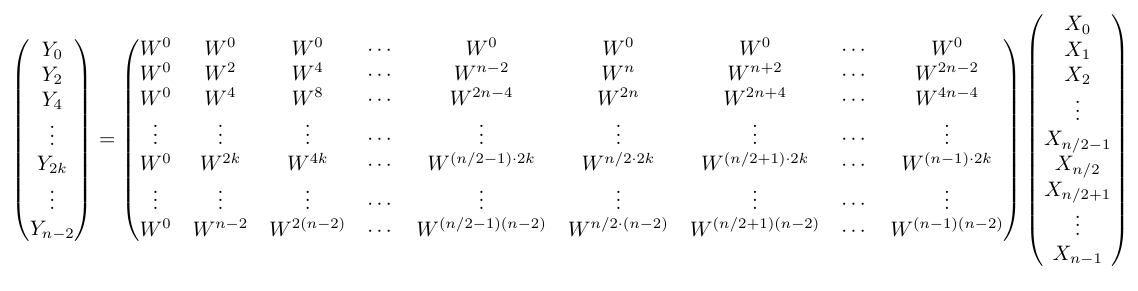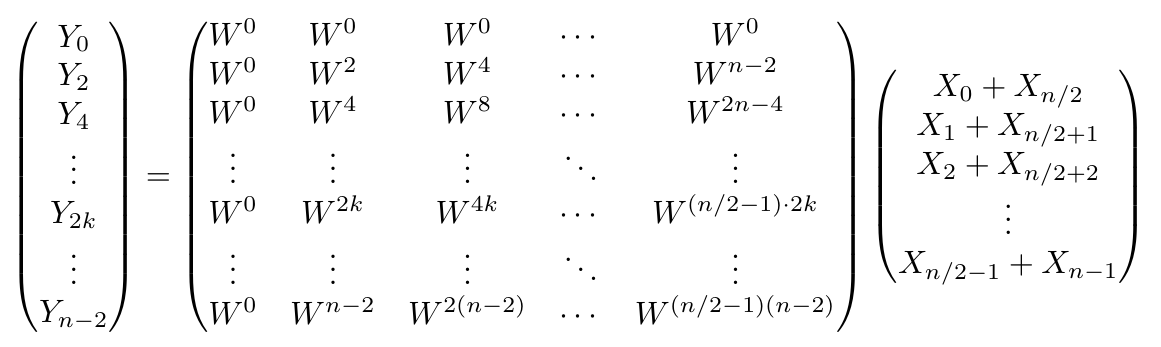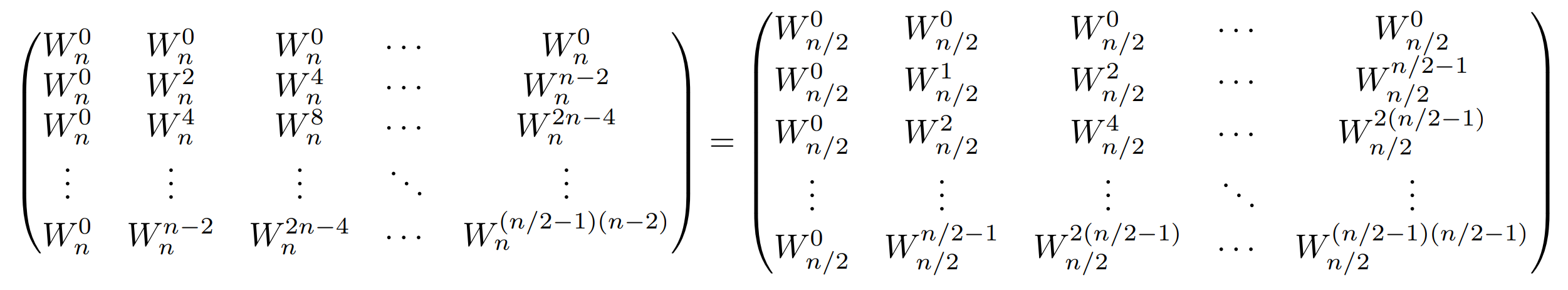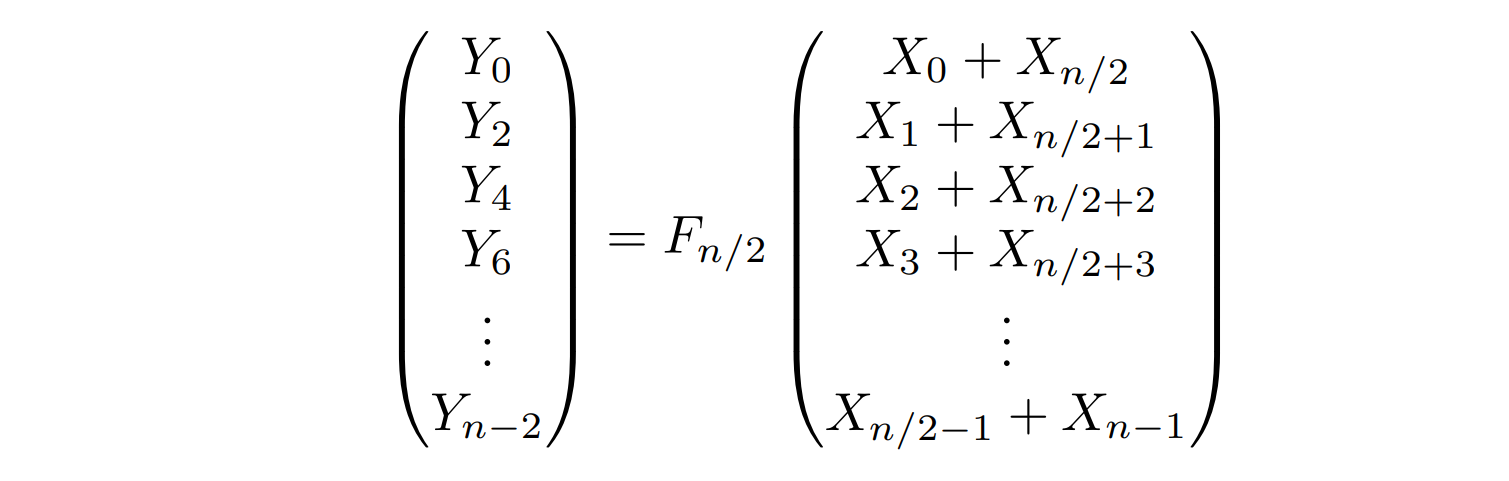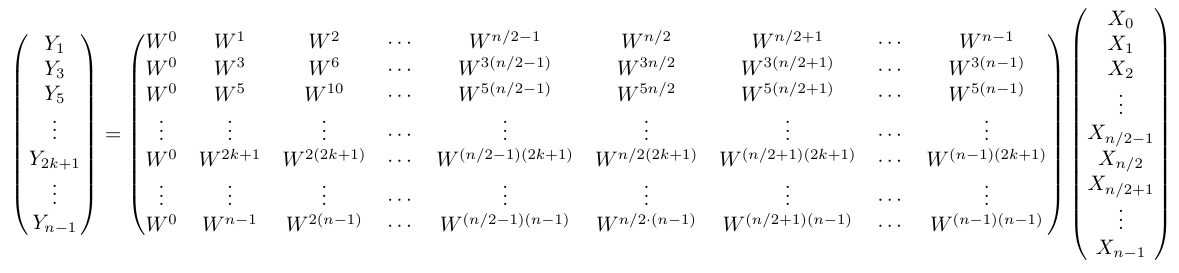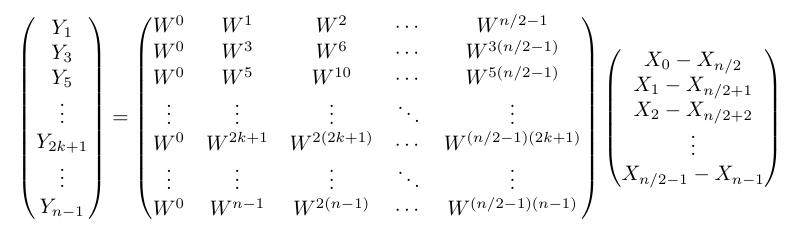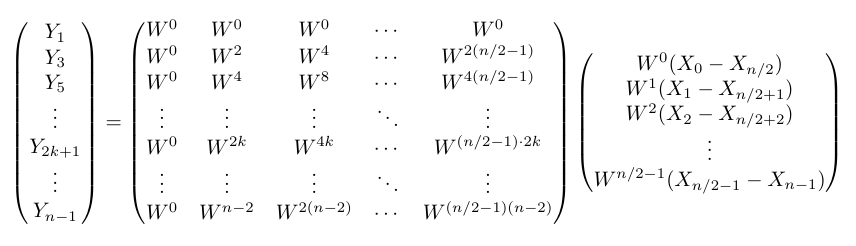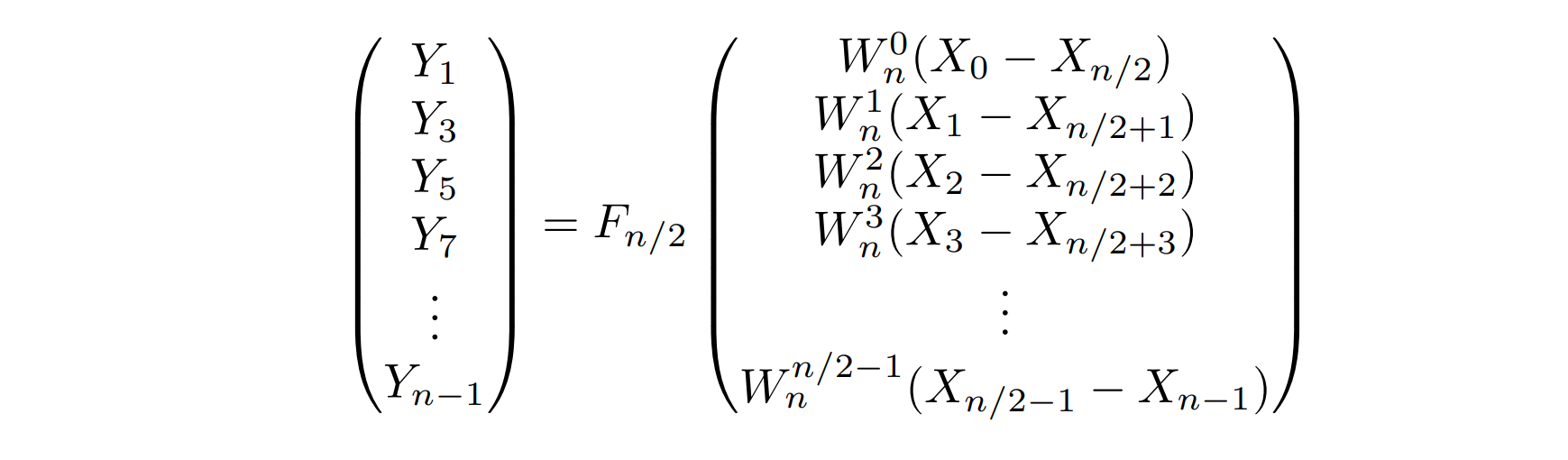この記事は、東京大学応用物理系2学科(物工/計数)のアドカレに向けて、昔書いた競技プログラマー向けのFFTの話を書き直したものです。
1. はじめに
この記事は、信号処理の方面ではよく紹介される、行列を使った 高速フーリエ変換(FFT) の理解と、競技プログラミングで使う 畳み込み の文脈のギャップを埋めることを目的にしたものである。
「フーリエ変換」と言えば、信号を周波数に分解するイメージがある人が多いだろう。しかし、競技プログラミングではやや異なる文脈で紹介される。それは、高速フーリエ変換(FFT)による畳み込みである。
信号処理の文脈でもFFTはよく出てくる。これは、「離散フーリエ変換(DFT)によって周波数領域に変換する」という操作を早くすることが目的だ。一方で、競プロでは畳み込みをすることが最終目的となるから、「DFTとは何なのか?」「なぜDFTをするのか?」という部分を補わないといけない。
ところで、競技プログラミングにおけるFFTの紹介は、慣例なのか分からないが、しばしば総和記号で表した式を繰り返し変形することによって説明される。
\hat{f}(t)=\sum_{i=0}^{n-1}f(\zeta_n^i)t^i
f(t)=\frac{1}{N}\sum_{i=0}^{n-1}\hat{f}(\zeta_n^{-i})t^i
こういった式に対して変形を繰り返して、DFTとその逆変換を説明し、さらに総和記号を前半と後半に分割してFFTを紹介する。もちろん原理としては間違っていないが、これだけを見ていても結局よく分からないという人も多いだろう。
そこで、別の見方を紹介する。競プロの文脈ではあまり紹介されていないような気がするが、信号処理などでは行列を使う説明が多く、これにより解像度がグッと上がる。結局DFT(IDFT)は行列の掛け算、FFTは行列の掛け算を高速化するアルゴリズムである。これを、競技プログラミングの文脈の下で説明しなおそうと思う。
前提知識
- 複素数平面、1の$n$乗根
- 行列(計算方法、結合法則、単位行列、逆行列が分かればOK)
行列の込み入った内容(線形独立性など)の知識がなくても式変形は追えるので、意欲的な高校生も理解できると思う。
2. FFTとは
高速フーリエ変換(FFT)とは、離散フーリエ変換(DFT)や逆離散フーリエ変換(IDFT)を高速に求めるアルゴリズムである。DFT・IDFTがやりたいこと、FFTがその手法。「並べ替え」と「マージソート」のような関係だ。
DFT・IDFTというのは、競プロにおいては「畳み込み」という演算に使う技術である。フーリエ変換というと、音声信号などを周波数の成分に分けるイメージがあると思うが、それと同じ操作を使うと畳み込みが便利に書けるという性質があるから、それを使っているのだ。畳み込みとは、2つの数列 $A,B$ があった時、以下のような要素からなる数列 $C$ を求める操作(あるいは求めたもの)である。
c _ k = \sum _ {j=0}^ {k} a _ jb _ {k-j} \hspace{10pt}(k=0,1,2\dots)
添え字の和が $k$ になるものについて積を取って足し上げる、という感じだ。
これは、多項式乗算としても言い換えられる。$ x^ j$の係数が$ a _ j$であるような多項式を$ A(x)$、$ b _ j$であるような多項式を$ B(x)$とし、$C(x)=A(x)B(x)$すると、$C(x)$の$ x^ k$の係数 $c _ k$ は $ a _ 0b _ k+a _ 1b _ {k-1}+a _ 2b _ {k-2}+…+a _ {k-1}b _ 1+a _ kb _ 0$となる。これは、まさに畳み込みである。
こういう問題が、例えばこういう形で出てくる。→ https://atcoder.jp/contests/atc001/tasks/fft_c
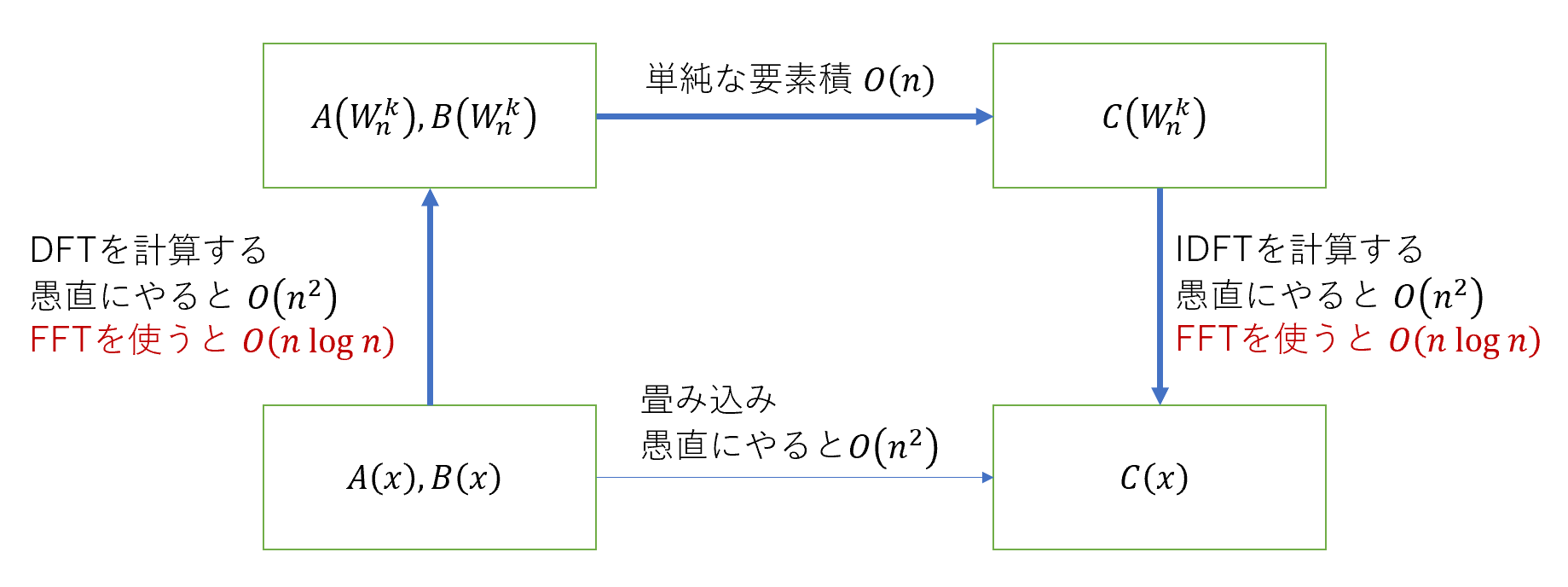
愚直に計算すれば、配列のサイズ(多項式の次数)を$n$として$O(n^2)$だが、DFTやIDFTという操作を経由することで高速に計算することができる。以下に模式図を示す。これから、多項式の乗算としてこの問題を考えていくことにする。
3. 畳み込みのためのDFT・IDFT
このパートではDFTとIDFTの定義から入るのではなく、「要は何をしたいのか」から見ていく。今求めたいのは $C(x)=A(x)B(x)$ である。
とりあえず解きやすくするために、高次項をゼロで埋めて、$A(x),B(x),C(x)$ を $n-1$ 次多項式として扱おう。
\begin{matrix}
A(x)=a _ 0+a _ 1x+a _ 2x^ 2+a _ 3x^ 3+\cdots +a _ {n-1}x^ {n-1} \\
B(x)=b _ 0+b _ 1x+b _ 2x^ 2+b _ 3x^ 3+\cdots +b _ {n-1}x^ {n-1} \\
C(x)=c _ 0+c _ 1x+c _ 2x^ 2+c _ 3x^ 3+\cdots +c _ {n-1}x^ {n-1} \\
\end{matrix}
同時に、ここに現れる係数を縦に並べた、以下のような列ベクトルを考えることにする。$a,b$ から $c$が求められれば多項式乗算(畳み込み)が完了したことになる。1
ここで、ある数$W _ n$を用いた、以下の$n$行$n$列の行列$ F_n$を考える。
つまり、$ j+1$行$ k+1$列が$ W _ n^ {jk}$であるような行列である。この$ W _ n$は信号処理の文脈で回転子と呼ばれるもので、複素数での1の$ n$乗根の一つ$ W _ n=\cos \frac{-2\pi}{n} +i\sin \frac{-2\pi}{n}$とするが、いったんは$ W _ n$という数であると思っていても問題ない。
いきなり変な行列が出てきて驚いたかもしれないが、これを使うととても便利である。$ F _ n a$ を考えよう。
これの計算結果は$ n$行からなる列ベクトルになるが、その上から$ j+1$行目は$ A(W _ n^ j)$になることが分かる(多項式として計算してあげれば良い)。よって、
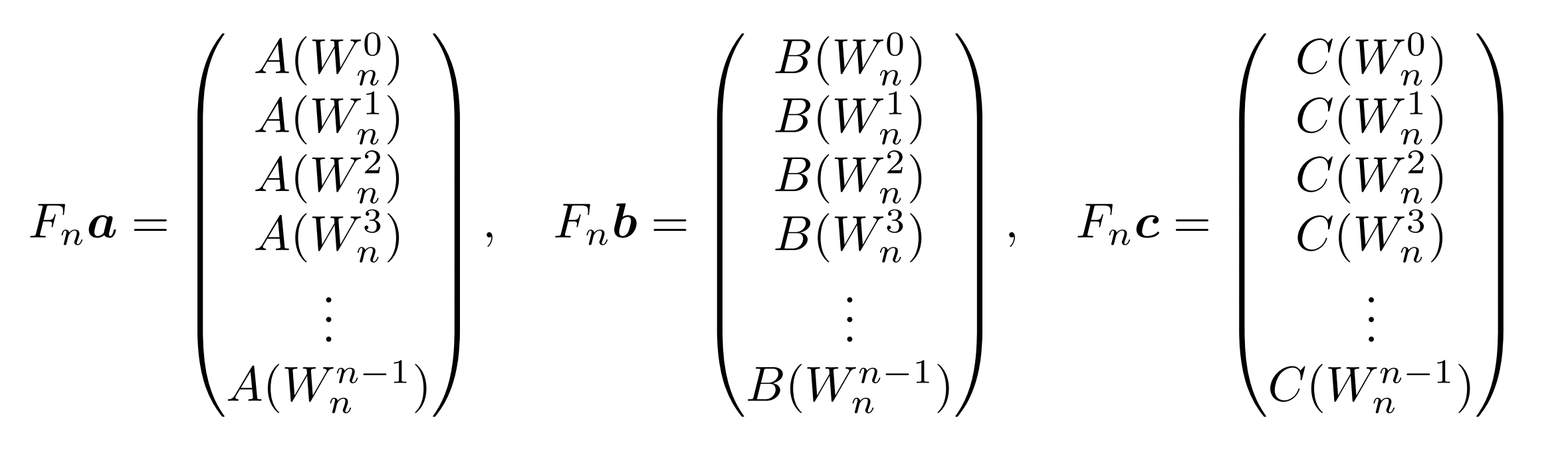
この行列$ F _ n$を掛ける操作(あるいは求めたもの)を、$a$や$b$の 離散フーリエ変換(DFT) と呼ぶ。また、$ F _ n$をDFT行列ということがある。
つまり、$A(x),B(x)$が与えられれば、$F _ n a$ と $F _ n b$ が分かり、さらに、$C(W_n^j)=A(W_n^j)B(W_n^j)$ より、$F _ n c$ を求めることができる。あとは、$F _ n c$ から $c$ を取り出せれば、$A(x),B(x)$ から $C(x)$ を求められる。(つまり$F_n$の逆行列が分かれば良い。)
そのために、以下のような$F_n^*$を考える。
これは、肩の指数が$-1$倍になったものだ。ここで、$W_n$が「$n$乗して初めて1になる数」であれば、以下が成り立つ。
だから$W_n$として複素数$\cos \frac{-2\pi}{n} +i\sin \frac{-2\pi}{n}$を用いるのである。
計算方法詳細
これより、$ j$行$ k$列の値は、
W _ n^ 0W _ n^ 0+W _ n^ {-j}W _ n^ k+W _ n^ {-2j}W _ n^ {2k}+ \cdots +W _ n^ {-j(n-1)}W _ n^ {k(n-1)}
=\sum _ {t=0}^ {n-1} W _ n^ {-jt}W _ n^ {kt}
=\sum _ {t=0}^ {n-1} W _ n^ {(k-j)t}
となる。これは初項$ 1$公比$ W _ n^ {k-j}$の等比数列の和だから、その値は
-
$ j=k$の時、$ n$ ($ W _ n^ {k-j}=1$となるため)
-
$ j≠k$の時、$0< |k-j|< n$ より $ W _ n^ {k-j}\neq 1$となるから、
\frac{1-(W _ n^ {k-j})^ n}{1-W _ n^ {k-j}}=\frac{1-(W _ n^ n)^ {k-j}}{1-W _ n^ {k-j}}=0
となる。(終)
$F_n^*F_n$が単位行列の$n$倍になることから、以下の式によって $c$ を復元できる。
このように$F_n^*$を掛ける操作(あるいはそれにより求めたもの)を 逆離散フーリエ変換(IDFT) と呼ぶ。
以上をまとめると、$ A(x)$と$ B(x)$から$ C(x)$を得る方法は、次のようになる。
-
DFTにより、$ n$個の値$ A(W _ n^ k)(k=0,1,2\cdots n-1)$及び$ n$個の値$ B(W _ n^ k)(k=0,1,2\cdots n-1)$を得る。
-
$ n$個の値$ A(W _ n^ k)B(W _ n^ k)(k=0,1,2\cdots n-1)$を得る。これは$ C(W _ n^ k)$に一致する。
-
IDFTによって$ C(x)$の係数を復元する。
手順の図を再掲する。DFT,IDFTは行列の積の演算だから、愚直にやると$ O(n^ 2)$ かかり、何も嬉しくない。しかし、 高速フーリエ変換(FFT) というアルゴリズムを使えば、この部分が$ O(n\log n)$まで削減できる。ここからは、FFTの紹介に移る。
回転子の偏角について
数論変換(NTT)について
例えば、$\mathrm{mod}$ $998244353$において、$(3^{119})^{8388608}\equiv 1$である。よって、回転子を$3^{119}$とすれば、$8388607$次多項式までに対して上と同様な操作を行うことができる。回転子を$43046721=(3^{119})^{16}$とすれば、$524287$次多項式までに対して上と同様な操作を行うことができる。なお、$8388608=2^{23}$であり、この2べきであるという性質はFFTにおいて活きることとなる。(原始根の値を誤っていたので直しました - 2023/12/16)
なんでこんな変形を思いつくんだ、という話(変形の解釈)
-
ここで現れたDFTは、「離散的な信号を、離散的な周波数として取り出す」という、信号処理の文脈でのれっきとした意味がある。一方で、「(連続関数の)畳み込みは、(連続的な)フーリエ変換をすると、単純な積になる」という性質があり、これは離散フーリエ変換においても成り立っている。だから、信号処理に使われがちな印象のあるフーリエ変換が、畳み込み演算という一見信号処理と関係ないところにも応用されているのである。
-
競技プログラミングの文脈におけるDFTの使い方は、「多項式の補間」と見ることができる。$A(W_n^k),B(W_n^k)$から$C(W_n^k)(k=1,2,\cdots,n)$を作り出す操作は、$n$個の点で$C(x)$を「評価」する操作と見ることができ、この情報を用いて$C(x)$の係数を復元する操作は、有限個の点から多項式$C(x)$を「補間」する操作と見ることができる。
-
あるいは、上で見た通り、$\frac{F_n}{\sqrt{n}}$はユニタリ行列であるから、DFTは座標変換と見ても良いだろう。
4. DFT・IDFTを高速に解くFFT
ここからがFFTである。だいたいここがこの記事の半分である。
FFTは$ n$が2のべき乗である時に機能する。ありうる多項式の次数を超える最小の2べきを選ぶことにしよう。
やりたいことを再確認する
まずDFTから考えよう。$ n$行の列ベクトル $a$ や $b$ に対してDFTを求めたい。これを一般化し、ある$n$行の列ベクトル$X$が与えられた時、$X$のDFTを求めることを考えたい。$X$のDFTを$Y$とし、$X,Y$の要素を$X_i,Y_i$と書けば、以下のようになる。
これを求める時、実はインデックスが偶数のものと奇数のものとで分けると、同じような計算が現れるのでまとめることができ、計算量を落とせるのだ。$ n=2$の場合は単純に$2\times2$の行列と$2$行の列ベクトルを計算すれば良いので簡単だから省略し、$ n≧4$として偶奇に分けて考える。
偶奇に分ける① インデックスが偶数のもの
$Y_i$のうちインデックス$i$が偶数のものを全て抜き出してみると以下のようになる。見づらいので、一旦$ W$の右下の添字は省略する。
ここで、行列の右半分(下図の赤枠)に注目する。すると、$ W _ n ^ n =1$という性質より、という性質より、行列の右半分(赤枠)が左半分(青枠)と全く同じ形をしていることが分かる。例えば、$ k$行目の左から$ n/2+2$列目は、
W _ n^{(n/2+1)2k}=W_n^{nk+2k}=W_n^{2k}
となるから$ k$行目の$ 1$列目に等しい。全ての列で同様のことが成り立つ。
そこで、これをまとめよう。行列の右半分を左半分にスライドさせると同時に、右側の列ベクトル$ X$の下半分(赤枠に対応)を上半分(青枠に対応)にスライドさせるようなイメージで、以下のようにまとめることができる。
ここで、$W _ n=\cos \frac{-2\pi}{n} +i\sin \frac{-2\pi}{n}$より、$W_n^2=W _ {n/2}$である。「$n$乗して初めて$1$になる数」を$2$乗すれば、「$n/2$乗して初めて$1$になる数」になる、という風に考えると良い。
よって、上に書いた行列は以下のように変形することができる。少々見づらいが、上記の式を用いて書き換えただけである。
よく見ると、これは$F_{n/2}$になっている。つまり、もともと求めたかったDFTの半分のサイズのDFTになっているのである!
これを$Y’=F_{n/2}X’$と書いておこう。
偶奇に分ける② インデックスが奇数のもの
インデックスが奇数の場合も同じことができそうだ。同様に$ Y$のうちインデックスが奇数のものを全て抜き出してみると以下のようになる。見づらいので、一旦$ W$の右下の添字は省略する。
ここで、行列の右半分(下図の赤枠)に注目する。すると今度は、$ W _ n ^ {n/2} =-1$という性質より、行列の右半分(赤枠)が左半分(青枠)の$-1$倍と全く同じ形をしていることが分かる。例えば、$ k$行目の左から$ n/2+2$列目は、
W _ n^{(n/2+1)(2k+1)}=W_n^{nk+2k+n/2+1}=-W_n^{2k+1}
となるから$ k$行目の$ 2$列目の$-1$倍に等しい。偶数の場合と同様、全ての列で同様のことが成り立つ。
そこで、これをまとめよう。これも、行列の右半分を左半分にスライドさせると同時に、右側の列ベクトル$ X$の下半分を上半分にスライドさせるようなイメージでいい。$-1$倍になることに注意すれば、以下のようにまとめることができる。
さらに、偶数の時と同様に「サイズが半分のDFTの形にしたい」というモチベーションで、以下のように変形できる。$ W ^ 0, W ^ 1, W ^ 2\cdots$を右側の列ベクトルに移したのだ。これが上の式と等しいと直感的に分からない場合は、各行について計算すれば確認できる。
さて、この式の右辺にある行列は偶数の時にも出てきた。よって、この行列を同じように変形をすれば、以下のようにサイズが半分のDFTの式を得る。
これを$Y’'=F_{n/2}X'’$と書いておこう。
DFTまとめ
以上より、サイズが$ n$のDFTは、
- 受け取った$ X$から、列ベクトル$ X', X''$を計算する。$ O(n)$。
- $ Y'$を$ X’$のDFT、$Y''$を$X'’$のDFTとして求める(両方ともサイズは半分)。
- $ Y', Y''$を組み合わせ、$ Y$を作り上げる。$ O(n)$。
として解くことができる。このように、問題の小さいサイズに分割して、それによって求めたものを用いて大きいサイズの問題を解く手法は、一般に分割統治法と言われる。FFTは要するに、分割統治法によって特別な形の行列の積を早く計算するアルゴリズムである。問題を半分ずつに分けて計算していくので、全体の計算量は$O(n\log n)$となる。マージソートの計算量解析と同様に考えれば良い。
IDFTへの流用
IDFTも考えなければならない。しかし、DFTが終わればほぼIDFTも終わっていると言える。
DFTが行列$ F$を掛けるのに対し、IDFTは$ F^*$を掛けて$ n$で割る。$ F$と$ F'$の違いは$ W _ n$の1乗を使うか、マイナス1乗を使うかだけだ。また、上のDFTの議論で使った以下の性質
- $ W _ n$は1の$ n$乗根
- $ W_n^2=W _ {n/2}$は$1$の$ n/2$乗根
- $ W _ n^ {n/2}=-1$
- $ n=2$の場合の計算($1,-1$しか現れない)
などは、$ F$を$ F^*$に変えても(つまり$ W _ n$を$ W _ n^ {-1}$に変えても)維持される。よって、$ X''$に現れる$ W _ n$を$ W _ n^ {-1}$に置き換えて、DFTと同じステップを踏み、最後に$ n$で割るだけ、という流れで、DFTを流用してIDFTが実行できてしまうのだ。
以上が、DFT・IDFTを高速で求めるFFTというアルゴリズムの全体像である。
さて、残りは実装だ。
数論変換(NTT)について
FFTは三角関数を使う関係上、浮動小数点数の演算が必要になり、値が大きくなるとどうしても誤差が生じてしまう。そのため、誤差を生じさせたくない時は、$\mathrm{mod}$ $998244353$上でNTTを行うという手もある。ただし、$\mathrm{mod}$ $1000000007$では、$n\geq 4$の2べきにおける$n$乗根が存在しないので、このままではまともに利用できない。そういった意味で、$998244353$は$8388608=2^{23}$乗根まで存在するので、NTTとの相性が良いのである。(これ以上の詳細は他に譲る。NTT,原始根などで調べてみると良い。)
5. 実装
再帰関数を使えばよく、以下のように実装できる。時間も空間も計算量は$O(n\log n)$である。ここまでの説明に忠実に書いたため、空間計算量は無駄が多くなったが、少し工夫すれば空間計算量を$O(n)$に落とせる。
ここまでの説明に従った実装例(C++)
#include <bits/stdc++.h>
using namespace std;
using cplx = complex<double>;
const double pi = acos(-1);
cplx W(double x, double y, bool inv) {
//偏角2πx/yの複素数
double arg = 2.0 * pi * x / y;
if (inv) return { cos(arg),sin(arg) };
else return { cos(arg),-sin(arg) };
}
void DFT(vector<cplx>& Q, int N, bool inv = 0) {
//QのDFTを計算する。結果はそのままQに入れる。
//inv=1ならIDFTを計算する
//N=2の場合は別に処理
if (N == 2) {
cplx s = Q[0] + Q[1], t = Q[0] - Q[1];
Q[0] = s, Q[1] = t;
return;
}
vector<cplx> E(N / 2), O(N / 2);
for (int i = 0;i < N / 2;i++) {
//E[i]は説明のX'に対応
E[i] = Q[i] + Q[i + N / 2];
//O[i]は説明のX''に対応
//W(i, N, inv) は、回転子のi乗
//inv=0ではDFT、inv=1ではIDFT
O[i] = (Q[i] - Q[i + N / 2]) * W(i, N, inv);
}
//偶数行目と奇数行目のそれぞれについて、サイズが半分のFFTを計算
//E,OにDFTの結果(説明のY',Y''に対応)がそのまま入る
DFT(E, N / 2, inv);
DFT(O, N / 2, inv);
for (int i = 0;i < N / 2;i++) {
//偶数行目と奇数行目にそれぞれの結果を入れていく
Q[i * 2] = E[i];
Q[i * 2 + 1] = O[i];
}
return;
}
void IDFT(vector<cplx>& Q, int N) {
DFT(Q, N, 1);
//IDFTではNで割る
for (int i = 0;i < N;i++)Q[i] /= (double)N;
}
int main() {
int N;
cin >> N;
int n = N * 2;
//nを超える最小の2べきを計算
n |= (n >> 1);n |= (n >> 2);n |= (n >> 4);n |= (n >> 8);n |= (n >> 16);n++;
vector<cplx> A(n, 0), B(n, 0), C(n, 0);
//多項式の係数(あるいは、畳み込みたい配列)を受け取る
for (int i = 1;i <= N;i++) {
cin >> A[i] >> B[i];
}
//受け取った多項式のDFTを計算
DFT(A, n);
DFT(B, n);
//要素積を単純計算
for (int i = 0;i < n;i++)C[i] = A[i] * B[i];
//IDFTを計算
IDFT(C, n);
//結果を出力(浮動小数点数で計算しているので、誤差が影響しないように+0.5する)
for (int i = 1;i <= 2 * N;i++)cout << (int)(C[i].real() + 0.5) << endl;
}
FFTの空間計算量を削減するやり方は様々あるが、よく見られるのが、$Y’,Y’’$を求めた後で偶数行目と奇数行目の並べ替えを省略するというやり方である。この手法を使うと、計算結果の配列では結果がビットリバース順に並ぶことになる。ビットリバースとはその名の通りビットを逆順にしたものである。例えば、サイズ8のFFTでは、
(0,1,2,3,4,5,6,7)_{(10)}=(000,001,010,011,100,101,110,111)_{(2)}
のビットリバースは
(0,4,2,6,1,5,3,7)_{(10)}=(000,100,010,110,001,101,011,111)_{(2)}
である。ビットリバース順になる理由は、「偶数行目と奇数行目を分ける」という操作が下の桁から行われるため、入れ替え操作がなければ下のビットから見て辞書順に並べられるからである。
このことが分かっていれば、並べ替える作業を省いて、最後に結果を取り出す順番を工夫するだけで済む。しかも、演算の途中は、計算結果を保存しておく配列を別途用意しておく必要はなく、配列を書き換えながらIn-placeに求めることができる。このような演算のやり方をバタフライ演算と言う。並べ替えを省略し、非再帰にして、ビットリバース順に取り出すアルゴリズム全体をCooley-Tukey型FFTと言うようだ。
ビットリバース・非再帰化の実装例(C++)
#include <bits/stdc++.h>
using namespace std;
using cplx = complex<double>;
const double pi = acos(-1);
vector<int> bit_reverse;
cplx W(double x, double y) {
double arg = 2.0 * pi * x / y;
return { cos(arg),-sin(arg) };
}
vector<cplx> convolution(vector<cplx>& A,vector<cplx>& B,int n){
cplx s,t,w;
int b=n/2;
//DFT
//b個隣同士でバタフライ演算を繰り返す
while(b){
for(int i=0;i<n;i+=b*2){
for(int j=i;j<i+b;j++){
w = W(j-i,b*2);
s = A[j];
t = A[j + b];
A[j] = s+t;
A[j + b] = (s-t)*w;
s = B[j];
t = B[j + b];
B[j] = s+t;
B[j + b] = (s-t)*w;
}
}
b/=2;
}
//A[i],B[i]はビットリバース順になっているので、ビットリバース順に取り出す
vector<cplx> C(n);
for(int i=0;i<n;i++)
C[bit_reverse[i]]=A[i]*B[i]/(double)n;
//IDFT
b=n/2;
while(b){
for(int i=0;i<n;i+=b*2){
for(int j=i;j<i+b;j++){
w = W(-(j-i),b*2);
s = C[j];
t = C[j + b];
C[j] = s+t;
C[j + b] = (s-t)*w;
}
}
b/=2;
}
//ビットリバース順になっていることに注意
return C;
}
int main() {
int N;
cin >> N;
int n = N * 2;
n |= (n >> 1);n |= (n >> 2);n |= (n >> 4);n |= (n >> 8);n |= (n >> 16);n++;
vector<cplx> A(n, 0), B(n, 0);
for (int i = 1;i <= N;i++) {
cin >> A[i] >> B[i];
}
//ビットリバースを計算
bit_reverse.resize(n,0);
for(int i = 0;i < n;i++){
for(int k = 1;k < n;k *= 2){
//iにおいて、kのbitが立っていたら、
//ビットリバースでは、n/(2k)のbitが立っている
if(i & k){
bit_reverse[i] += n / (2 * k);
}
}
}
vector<cplx> ans = convolution(A,B,n);
//ビットリバース順に取り出して出力
for (int i = 1;i <= 2 * N;i++)
cout << (int)(ans[bit_reverse[i]].real() + 0.5) << endl;
}
これにより、時間のオーダーは変わらないが、定数倍がかなり改善する。実は畳み込みをするだけならビットリバース順を求めることすら不要なのだが、それは別の機会としよう。
6. 最後に
行列は視覚的に分かるので本当に理解の助けになると思うので、使わない手はない。DFTとIDFTの関係とか、添字をずらしてまとめて半分のサイズにするとか、絶対に行列の方が見通しが良いし本質的だと思うので、この考え方を標準に据えた方が良いと私は思う。競技プログラマー向けに行列で説明した記事は他にもあるかもしれないが、行列で説明する記事が増えた方が良いので、私もこのように記事を一つ拵えたということである。
FFTを理解したいなら行列を使え!
参考にしたもの
大学受験直後に背伸びして 「道具としてのフーリエ解析」 (第7刷 著者:涌井良幸・涌井貞美 発行:日本実業出版社) を買ったのが理解に大きく寄与していると思う。高校生でも入りやすい。
-
本来は太字にした方が良いが、QiitaのMarkdownでの数式の書き方に慣れていないので通常の太さにした(怠惰)。同じ理由で、記事内の数式はTeXで打って画像化して埋め込んだものが多くなった。 ↩