【流体シミュレーション ベンチマーク】テイラーグリーン渦 pythonコード

テイラーグリーン渦とは

流体シミュレーションでは、微分方程式である支配方程式（＝物理法則）を数値的に解くことで速度や圧力などの値を算出します。具体的には$(\ref{xeq})$$(\ref{yeq})$のナビエストークス方程式のｘｙ方向の運動方程式と$(\ref{coneq})$の連続の式を数値的に解きます。

$$
\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{1}{\rho}\frac{\partial p}{\partial x}+\nu\biggl(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}\biggr)\label{xeq}\tag{1}
$$
$$
\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=-\frac{1}{\rho}\frac{\partial p}{\partial y}+\nu\biggl(\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2}\biggr)\label{yeq}\tag{2}
$$

$$
0=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\label{coneq}\tag{3}
$$
このように微分方程式を解くのには理由があります、その理由はこれらの式を満たす一般解が存在しないためです。
ただし、ある条件下においてのみ解（解析解）は存在します、その一例が今回ご紹介するテイラーグリーン渦になります。

テイラーグリーン渦の解析解

0<x,y<2πの２次元領域においてテイラーグリーン渦の解は以下の式となります。
この式により任意の点と座標における速度と圧力が数式により求められるため、実験データなどを用いなくともシミュレーションの妥当性を検証が可能です。
これは特に時間変化を伴う非定常モデルにおいてベンチマークとして使われています。
$$
u(t)=\sin(x)\cos(y)F(t)
$$
$$
v(t)=-\cos(x)\sin(y)F(t)
$$
$$
p=\frac{\rho}{4}(\cos(2x)+\cos(2y))F^2(t)
$$

Pythonコード

taylor-green.py

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from matplotlib.gridspec import GridSpec

# パラメータ
L = 2 * np.pi  # 領域サイズ
N = 128        # グリッドポイント数
dx = L / N     # グリッドサイズ
dt = 0.1       # タイムステップ
T = 10.0        # 合計時間
frames = int(T / dt)# フレーム数
nu=0.1 # 動粘性係数
u_min,u_max=-1,1 # x方向速度の最大最小値
v_min,v_max=-1,1 # y方向速度の最大最小値

# グリッドセットアップ
x = np.linspace(0, L, N, endpoint=False)
y = np.linspace(0, L, N, endpoint=False)
X, Y = np.meshgrid(x, y)

def taylor_green_vortex(X, Y, t, k=2):
    """Generate the Taylor-Green vortex at time t."""
    u = np.sin(X) * np.cos(Y) * np.exp(-2*nu*t)
    v = -np.cos(X) * np.sin(Y) * np.exp(-2*nu*t)
    return u, v

def update(frame):
    """Update the plot for each frame."""
    plt.clf()
    u, v = taylor_green_vortex(X, Y, frame * dt)
    
    # x方向速度のプロット
    ax1 = plt.subplot(gs[0, 0])
    c1 = ax1.contourf(X, Y, u, levels=50, cmap='RdBu_r', vmin=u_min, vmax=u_max)
    ax1.set_title(f'X Velocity (u) at t={frame * dt:.2f}')
    ax1.set_xlabel('x')
    ax1.set_ylabel('y')
    fig.colorbar(c1, ax=ax1,ticks=np.linspace(u_min, u_max, 11))
    
    # y方向速度のプロット
    ax2 = plt.subplot(gs[0, 1])
    c2 = ax2.contourf(X, Y, v, levels=50, cmap='RdBu_r', vmin=v_min, vmax=v_max)
    ax2.set_title(f'Y Velocity (v) at t={frame * dt:.2f}')
    ax2.set_xlabel('x')
    ax2.set_ylabel('y')
    fig.colorbar(c2, ax=ax2,ticks=np.linspace(v_min, v_max, 11))

# 描画とグリッドの作成
fig = plt.figure(figsize=(12, 6))
gs = GridSpec(1, 2, width_ratios=[1, 1])

# アニメーションの作成
ani = animation.FuncAnimation(fig, update, frames=frames, repeat=False)

# gifとして保存
ani.save('taylor_green_vortex.gif', writer='pillow', fps=10)

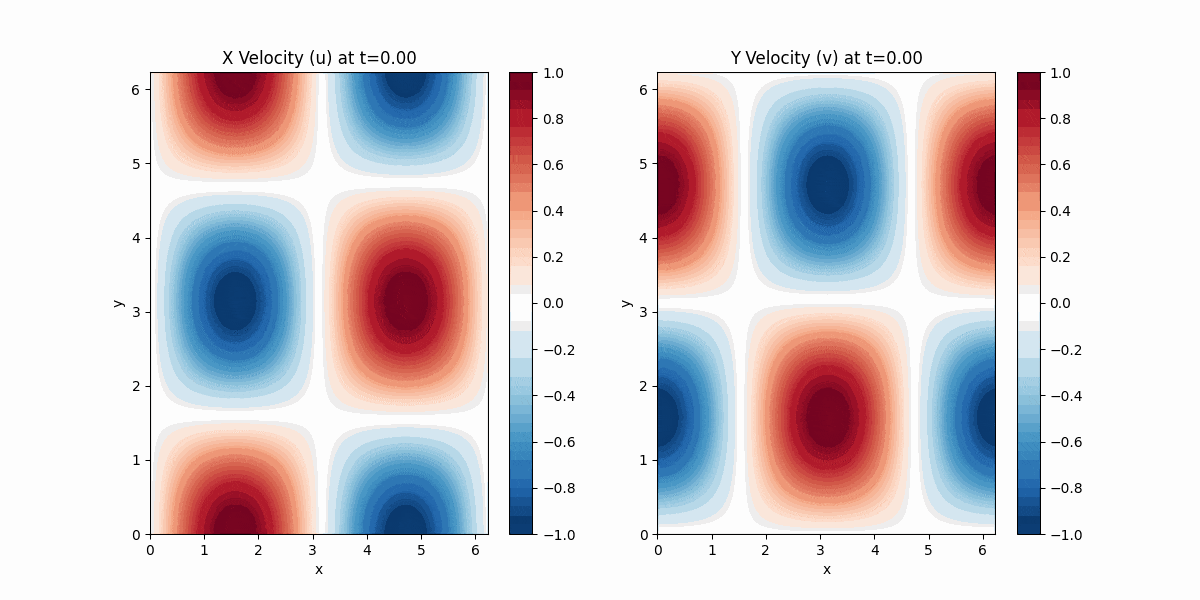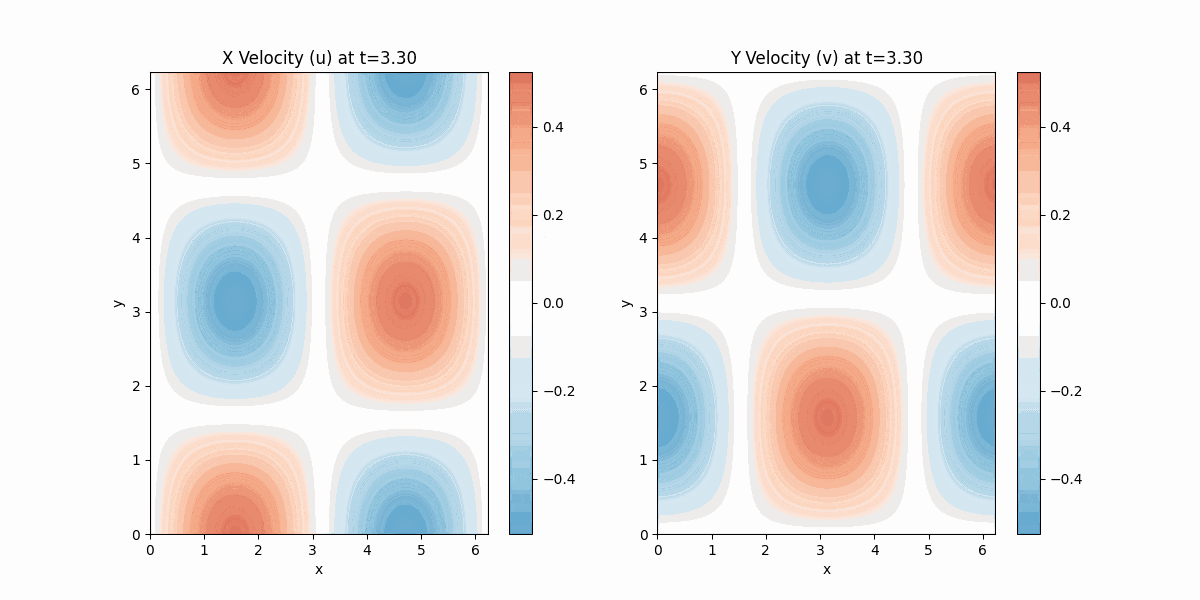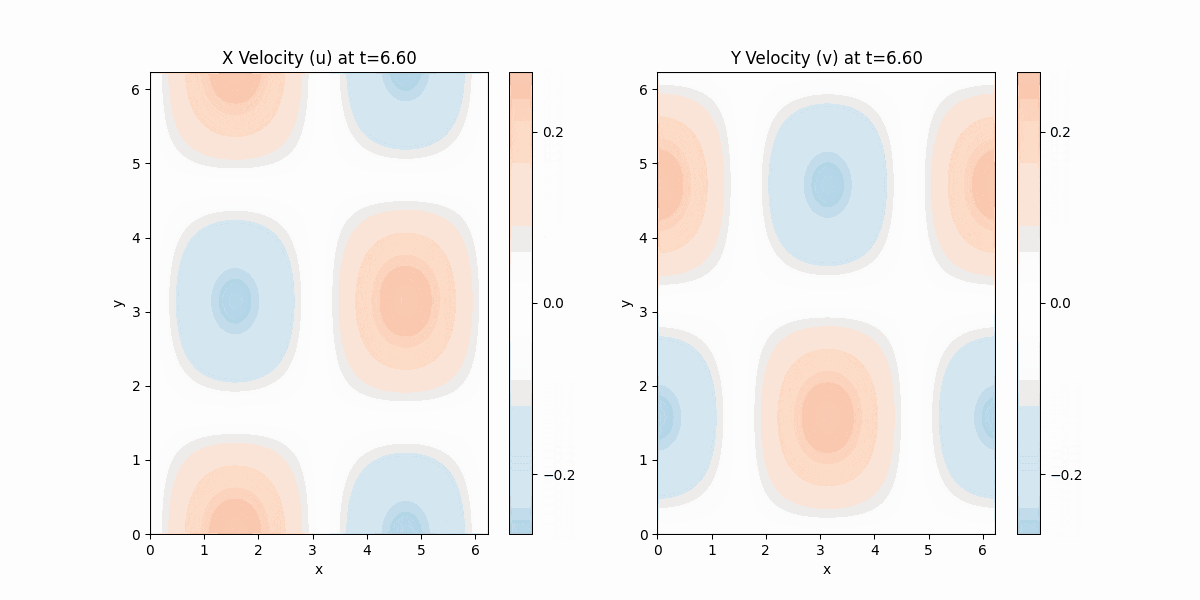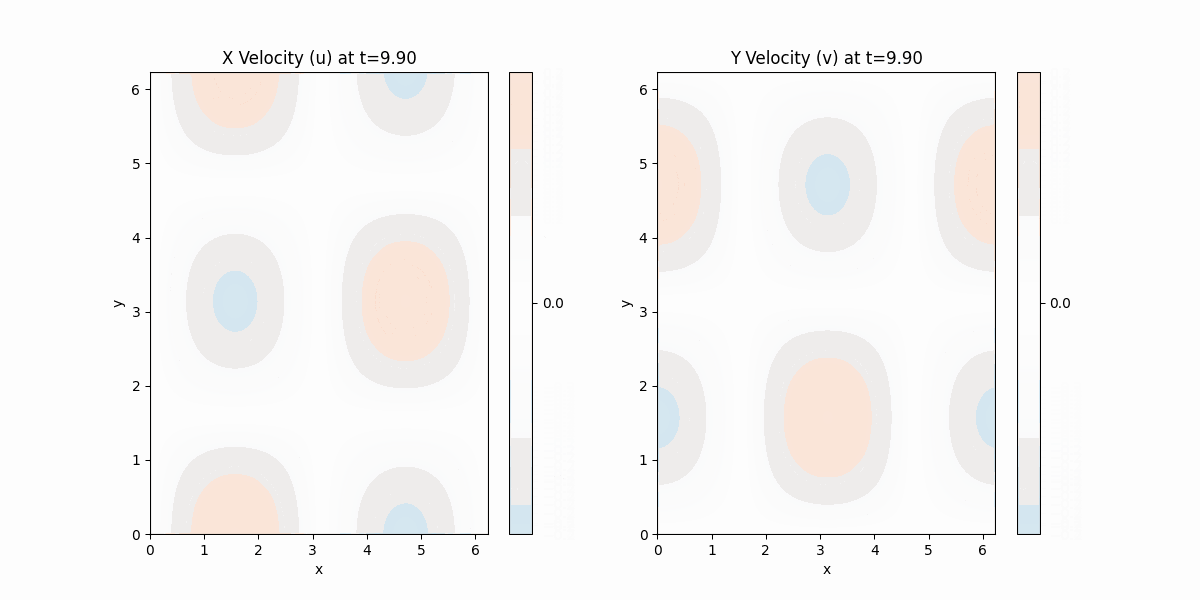
出力結果

まとめ

流体シミュレーションにおけるベンチマークであるテイラーグリーン渦について紹介させていただきました。
今後はこのベンチマークを用いて近年注目されている、AIでシミュレーションを行うサロゲートモデルの精度を比較していきたいと思います。