ChatGPT o3-mini が実現！p5.js で描く美麗な 3D 正二十四胞体シミュレーション

はじめに

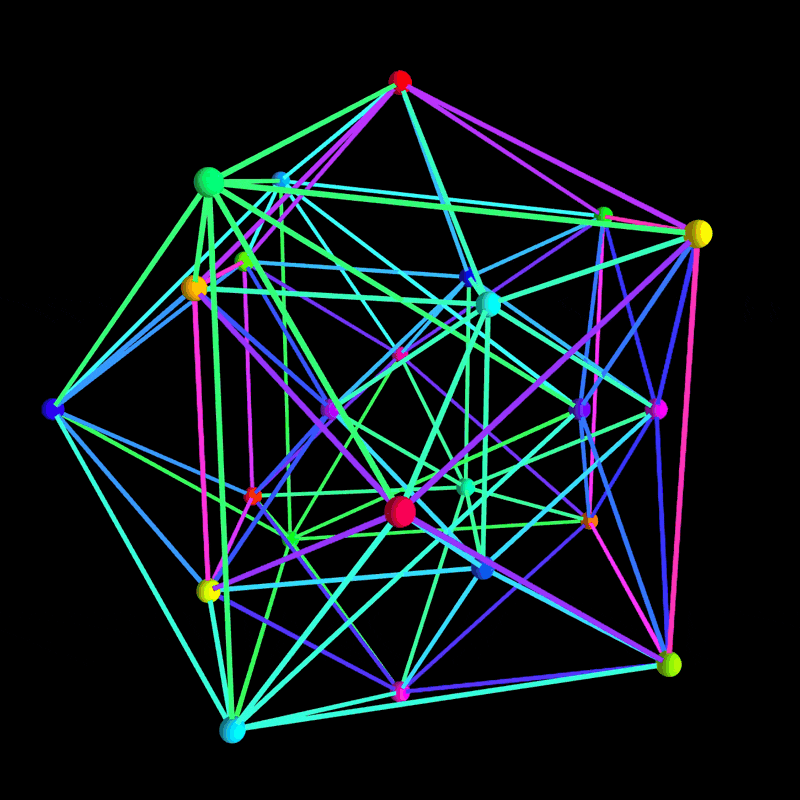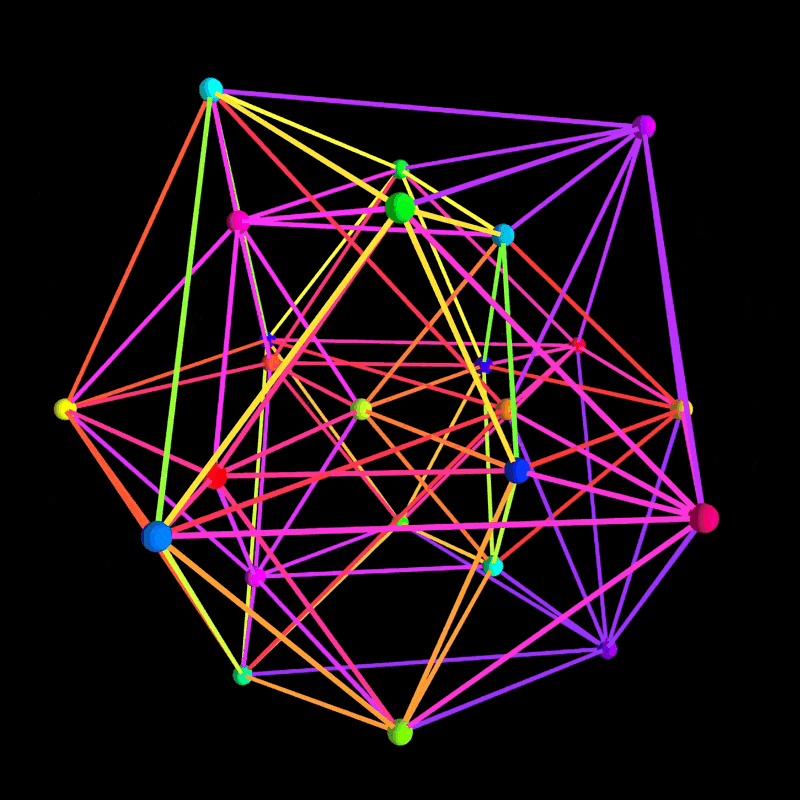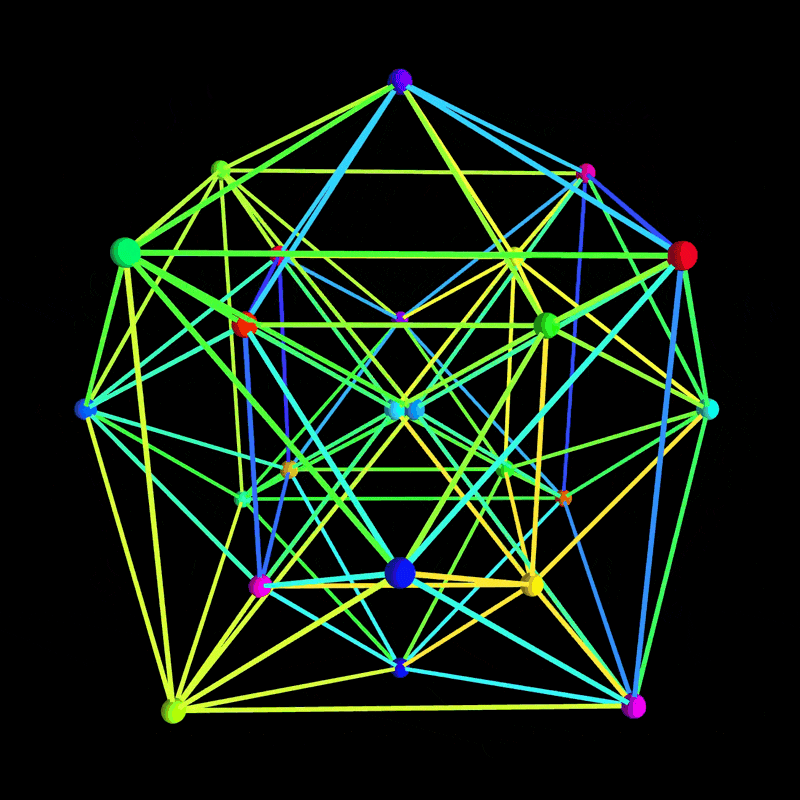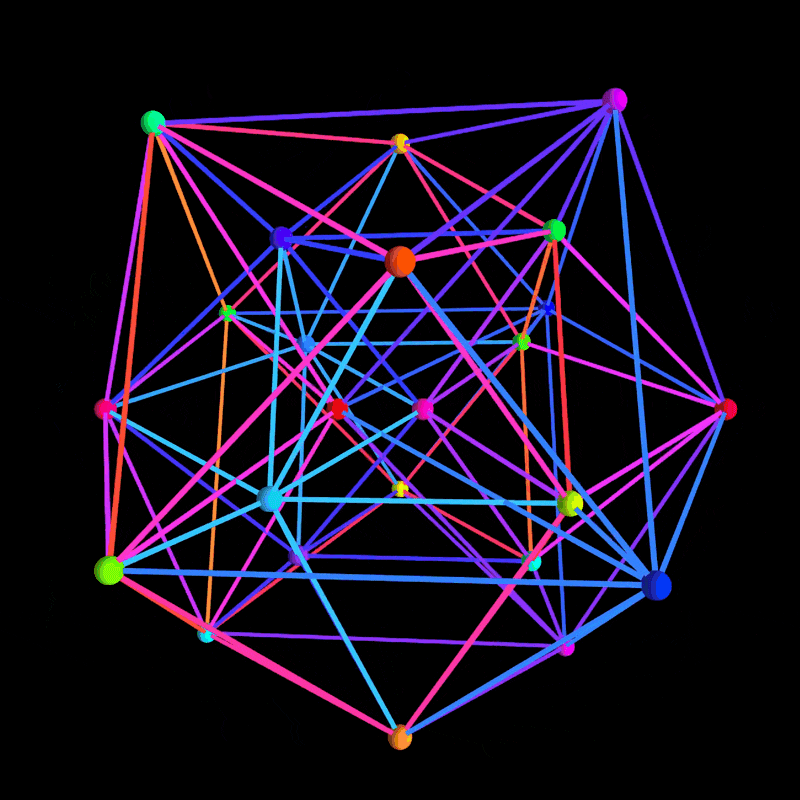
正二十四胞体（24-cell）は、四次元幾何学における非常に魅力的な多胞体です。今回の記事では、Wikipedia の 24-cell の記述を参考に、ChatGPT o3-mini により瞬時にかつノーミスで作成された、p5.js を用いた 3D シミュレーションプログラムをご紹介します。
p5.js の WEBGL モードを活用して、正確な幾何学表現とカラフルなエフェクト、さらにはユーザーインタラクションも実現しており、誰もがうっとりするほど美しいビジュアルを提供しています。

プログラムの概要

今回のシミュレーションプログラムでは、以下のポイントに重点を置いています。

• 正確な構造表現
  正二十四胞体の頂点は、(±1, ±1, 0, 0) の全組み合わせにより生成され、4 次元空間での回転と簡易的な遠近投影を用いて 3D 空間に射影します。エッジも 4 次元ユークリッド距離の計算に基づき正確に抽出されています。

• カラフルで魅惑的な描画
  HSB カラーモードを利用し、動的に変化するグラデーションや発光効果を適用。各エッジや頂点に対して多彩な色彩を割り当てることで、見る者を魅了するビジュアルを実現しています。

• インタラクティブな操作
  p5.js の orbitControl() により、ユーザーはマウスドラッグやキーボード操作を使ってシーンの回転、拡大縮小が可能です。また、時間経過に伴う自動回転アニメーションも取り入れ、動的な視点変更を楽しむことができます。

プログラムコード

以下は、実際に p5.js エディタ 上で動作するプログラムコードです。ChatGPT o3-mini により、ミスなく高品質なコードが瞬時に生成されました。

// 正二十四胞体 (24-cell) の 4D 頂点・エッジを 3D 表示する p5.js スケッチ

let vertices4D = [];  // 4次元頂点リスト（各頂点は [x, y, z, w] の配列）
let edges = [];       // 頂点インデックスのペア（エッジ）

function setup() {
  createCanvas(windowWidth, windowHeight, WEBGL);
  colorMode(HSB, 360, 100, 100, 100);
  // 正二十四胞体の頂点生成:
  // 頂点は (±1, ±1, 0, 0) の全順列（4 次元座標のうち、2 つが ±1、残りが 0）
  vertices4D = [];
  let vals = [1, -1];
  for (let i = 0; i < 4; i++) {
    for (let j = i + 1; j < 4; j++) {
      for (let a = 0; a < 2; a++) {
        for (let b = 0; b < 2; b++) {
          let v = [0, 0, 0, 0];
          v[i] = vals[a];
          v[j] = vals[b];
          vertices4D.push(v);
        }
      }
    }
  }
  
  // エッジの前計算:
  // 24-セルでは、各頂点は 8 本のエッジで他の頂点と接続しており、
  // 2 頂点間の 4 次元ユークリッド距離の二乗が 2 のとき（誤差を含む）エッジとみなす
  edges = [];
  for (let i = 0; i < vertices4D.length; i++) {
    for (let j = i + 1; j < vertices4D.length; j++) {
      let d2 = squaredDistance(vertices4D[i], vertices4D[j]);
      if (abs(d2 - 2) < 0.001) {  // 許容誤差
        edges.push([i, j]);
      }
    }
  }
}

function draw() {
  background(0);
  orbitControl();  // マウスによる視点操作を有効化

  // ダイナミックなライティング設定（シーンを立体的に演出）
  directionalLight(0, 0, 100, -1, 0, -1);
  ambientLight(50);
  
  // 時間経過に伴う 4D 空間内の回転角度（複数の回転面を利用）
  let angle = frameCount * 0.01;
  
  // 各頂点に対して、4D 回転を適用し 3D へ射影する
  let projected = [];
  for (let v of vertices4D) {
    let rotated = rotate4D(v, angle);
    let proj = project4Dto3D(rotated);
    projected.push(proj);
  }
  
  // エッジ描画（各エッジにカラフルな色と動的なシェードを適用）
  strokeWeight(2);
  for (let e of edges) {
    let i = e[0];
    let j = e[1];
    stroke((frameCount + i * 10) % 360, 80, 100);
    let v1 = projected[i];
    let v2 = projected[j];
    line(v1.x, v1.y, v1.z, v2.x, v2.y, v2.z);
  }
  
  // 頂点描画（小さな球体で表示）
  noStroke();
  for (let i = 0; i < projected.length; i++) {
    fill((frameCount + i * 15) % 360, 100, 100);
    let v = projected[i];
    push();
    translate(v.x, v.y, v.z);
    sphere(5);
    pop();
  }
}

// 4次元空間における2点間のユークリッド距離の二乗を計算
function squaredDistance(v1, v2) {
  let sum = 0;
  for (let i = 0; i < 4; i++) {
    let d = v1[i] - v2[i];
    sum += d * d;
  }
  return sum;
}

// 4D 回転: XW 平面と YZ 平面での回転を組み合わせる
function rotate4D(v, theta) {
  let x = v[0], y = v[1], z = v[2], w = v[3];
  
  // XW 平面での回転
  let cosA = cos(theta);
  let sinA = sin(theta);
  let x1 = x * cosA + w * sinA;
  let w1 = -x * sinA + w * cosA;
  
  // YZ 平面での回転
  let cosB = cos(theta * 0.5);
  let sinB = sin(theta * 0.5);
  let y1 = y * cosB - z * sinB;
  let z1 = y * sinB + z * cosB;
  
  return [x1, y1, z1, w1];
}

// 4D から 3D への透視投影
function project4Dto3D(v4) {
  let [x, y, z, w] = v4;
  // 遠近感を出すための投影距離（d は 4次元空間上の視点距離）
  let d = 3;
  let factor = d / (d - w);
  // スケーリングして見やすいサイズに調整
  let x3 = x * factor * 100;
  let y3 = y * factor * 100;
  let z3 = z * factor * 100;
  return createVector(x3, y3, z3);
}

function windowResized() {
  resizeCanvas(windowWidth, windowHeight);
}

実行環境と動作確認

このプログラムは、p5.js エディタ に直接貼り付けて実行可能です。
エディタ上で動作させると、以下の特徴が体験できます。

• 美麗な 3D 表現
  正二十四胞体の各頂点やエッジがカラフルに輝き、動的なライティングとシェーディングが加わることで、立体感あふれるビジュアルを楽しめます。

• インタラクティブな視点操作
  マウスドラッグやキーボード操作により、シーンの回転やズームが自由に行えます。ユーザーの操作に応じたダイナミックな視点変更が実現されています。

• 自動回転アニメーション
  時間経過に伴う回転によって、正二十四胞体の複雑な構造が動的に変化し、まるで夢のような映像を体験することができます。

まとめ

本記事では、ChatGPT o3-mini により瞬時にかつミスなく作成された、p5.js を使用した 3D 正二十四胞体シミュレーションプログラムを紹介しました。
Wikipedia の 24-cell の情報を参照しながら、高度な数学的概念を美麗なビジュアル表現へと昇華させた本プログラムは、そのクオリティの高さを実感いただける内容となっています。
ぜひ、p5.js エディタ 上でプログラムを実行し、その魅惑的な世界を体験してみてください。