概要
平方数の判定を mod を使うと効率よくできるという記事 を5年くらい前に @hnw が ブログでまとめてた 。私は 数論をあまり知らないので、手を動かしながら確かめたい(Python3 on Google Colab)。
「平方数の mod 256 の値は 44 種類しかない」という性質がある。
これを逆に使う。「ある数 N を mod 256 してみて 結果が 44 種類のどれにも該当しないなら Nは平方数でない」を判定の先頭に配置すると、 (256-44)/256 ≒ 83% くらいの確率で 平方数でないと早めに判定ができる。 mod 256 って結局 0xff との ANDというビット演算なので、高速で嬉しい。
44種類?
mod 256だと 44種類だし mod 100 だと 22種類だし(出典:Wikipedia)、mod 19 だと 10種類らしい。これを確かめよう。
全ての自然数について調べる必要はない。mod 256 で k となる数は、二乗したときに同じ値になるから(なぜなら $(Q\cdot 256+k)^2$ を 256 で割った余りは $k^2$ を256で割った余り となり $k$のみに依存し$Q$に依存しない)。つまり、0..255 の整数について二乗したときの余りを調べれば十分:
>>> set(map(lambda x: x * x % 256, range(0,256)))
{0, 1, 129, 4, 132, 9, 137, 16, 144, 17, 145, 25, 153, 33, 161, 36, 164, 169, 41,
49, 177, 185, 57, 64, 193, 65, 196, 68, 73, 201, 81, 209, 217, 89, 225, 97, 100,
228, 249, 105, 233, 113, 241, 121}
上記ワンライナーにより 確かに 44 種類しかないことがわかる。mod100についても同様に 22 種類だとわかる:
>>> set(map(lambda x: x * x % 100, range(0,100)))
{0, 1, 4, 9, 16, 21, 24, 25, 29, 36, 41, 44, 49, 56, 61, 64, 69, 76, 81, 84, 89, 96}
こうなると 色々な数について、この方法での効率を調べたくなってくる。
効率性の可視化
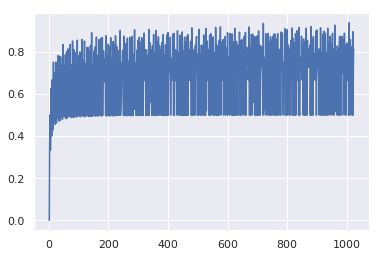
前章では mod 256 と mod 100 のみを調べた。そして mod 256 での効率がおおよそ 83% であることを見た。このパーセンテージは 高めたり低めたりすることができるのだろうか?というのを Google Colab で可視化してみた:
def efficiency (n):
L = len(set(map(lambda x: x * x % n, range(0,n))))
return float(n - L)/n
xs = list(range(2, 1024))
ys = list(map(efficiency, range(2, 1024)))
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
plt.plot(xs,ys)
チャートは以下のようになる:
ここから言えそうなのは
-
mod 256の 83% っていうのはまあ悪くない数字 - 数によって振れ幅があるけど 50% くらいに下限がある
ということくらいなので、以下若干の考察
83%→94%
どうも 1024 まで調べた範囲だと mod 1008 が一番高効率になり、そのときのパーセンテージは 94% 程度になった。
print (max(ys), ys.index(max(ys)))
print efficiency(1008)
# 0.9365079365079365 1006
# 0.9365079365079365
50%弱が下限で 素数だと下限に近い
これは hnw の記事でも指摘していた事象だと思う。つまり、mod 素数の時は、ちょうど半分が候補から外れることを反映している。以下より、たしかに 全ての素数の効率が 50% 以下であることがわかる:
def is_prime (n):
return all(map((lambda m: n % m != 0), range(2,n)))
zs = [ i+2 for i, y in enumerate(ys) if y < 0.5]
primes = list(filter(is_prime, range(3,1024)))
all(list(map(lambda p: p in zs, primes))) # true
逆に効率が低いからといって素数というわけではない
print (list(map(is_prime, zs)).count(True)) # 172
print (list(map(is_prime, zs)).count(False)) # 96
まとめ
平方数の判定に mod 256 を使うことで効率が上がりそうだということを確かめた。