Coq で命題論理（22個のトートロジー）

1. 概要

Coq で 命題論理のトートロジーを証明します。tauto でCoqが自動で証明してくれますが、Coqに親しむため手で証明します。古典論理を扱います。

1-1. 参考資料

以下の資料で勉強をしました

• 高橋研の授業資料 (PDF/日本語/50ページ程度)
  • Coq初心者だけど 論理学がある程度わかるなら この資料から入るのが一番やりやすいです
• Coq in a Hurry (PDF/英語/50ページ程度)
  • 上記の資料でざっくりわかったら、次にこの資料を読みます。知識の体系化や応用的なトピックにどのようなものがあるのかについてのとっかかりになります。演習問題の全てに解答が付いています。

1-2. チートシート

上述の『Coq in a Hurry』に掲載されているチートシートを引用します:

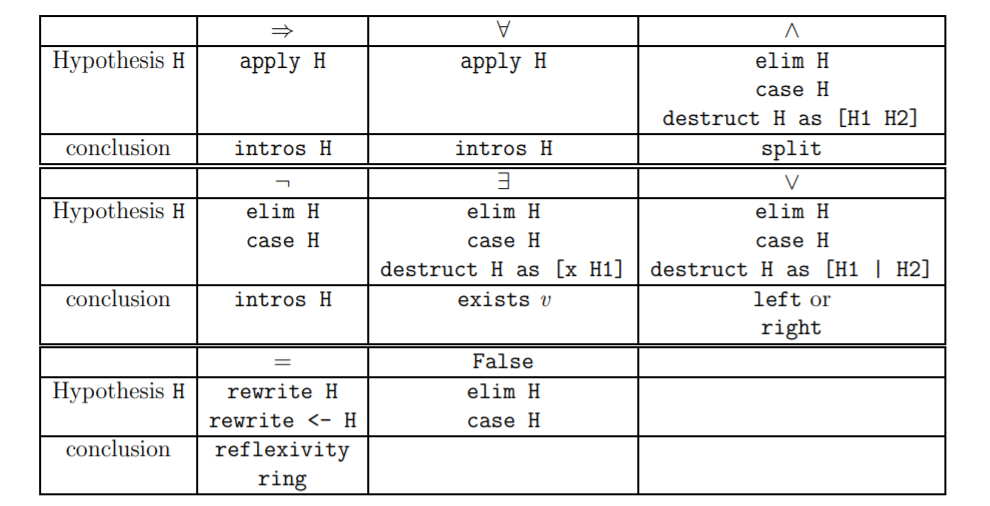
1-3. 古典論理

Coq での証明系は 直観主義論理( LJ 相当) です。排中律を公理として追加すると古典論理に一致します。そのために Require Import Classical というコマンドが必要です。例えば、二重否定除去・パースの法則などは Classical がないと証明できません。2-6で後述します。

• 参考: Classical の公式ドキュメント

1-4. 表記

$P,Q,R,S$ を命題変数とします。論理記号は $\lnot, \land, \lor, \to$ を使います。

2. トートロジーの証明

ファイル冒頭に以下の記述が必要です:

Require Import Classical.
Section XYZ.
Variable P Q R S: Prop.

2-1. 交換則など

当たり前のトートロジーも Coqなら新たな気づきがあります。以下のトートロジーを証明してみます:

• $P\land Q \land R \to Q \land (R \land P)$
• $P\lor Q \lor R \to Q \lor (R \lor P)$

Goal P /\ Q /\ R -> Q /\ (R /\ P).
intro H. destruct H as [H1 [H2 H3]].
split. assumption. split. assumption. assumption. Qed.

Goal P \/ Q \/ R -> Q \/ (R \/ P).
intro H. destruct H as [H1|[H2|H3]].
right. right. assumption. left. assumption. right. left. assumption. Qed.

ひとこと： destruct をまとめて行う方法を押さえておきたいです。あとはチートシートをみればすぐです。逆（$\leftarrow$）も同様に証明できます。

2-2. 分配則など その1

少しだけ非自明な分配則を証明してみます:

• $P\land(Q\lor R) \to (P\land Q)\lor(P \land R)$
• $P\lor(Q\land R) \to (P\lor Q)\land(P \lor R)$

Goal P /\ (Q \/ R) -> (P /\ Q) \/ (P /\ R).
intros H. destruct H as [H1[H2|H3]].
left. split. assumption. assumption. right. split. assumption. assumption. Qed.

Goal P \/ (Q /\ R) -> (P \/ Q) /\ (P \/ R).
intros H. destruct H as [H1|[H2 H3]].
split. left. assumption. left. assumption. split. right. assumption. right. assumption. Qed.

ひとこと: 論理和と論理積が入り混じっているときも destruct が有効に使えることがわかります。

2-3. 分配則など その2

含意 と 論理和/論理積 が絡んでくる分配則を覚えている人はそれほど多くない気がします。右分配則とよばれる後ろ二つは要注意です:

• $P \to (Q \land R) \to (P \to Q) \land (P\to R)$
• $P \to (Q \lor R) \to (P \to Q) \lor (P\to R)$
• $(Q \land R \to P) \to (Q \to P) \lor (R \to P)$ ＜古典論理＞
• $(Q \lor R \to P) \to (Q \to P) \land (R \to P)$

Goal P -> (Q \/ R) -> (P -> Q) \/ (P -> R). 
intros H1 H2. destruct H2. left. intro. assumption. right. intro. assumption. Qed.

Goal P -> (Q /\ R) -> (P -> Q) /\ (P -> R).
intros H1 H2. destruct H2. split. intro. assumption. intro. assumption. Qed.

Goal (Q /\ R -> P) -> (Q -> P) \/ (R -> P).
intros. apply imply_to_or in H. destruct H as [H1|H2].
apply not_and_or in H1. destruct H1. left. intro. contradiction. right. intro. contradiction.
left. intro. assumption. Qed.

Goal (Q \/ R -> P) -> (Q -> P) /\ (R -> P).
intros. split.
intro. apply H. left. assumption.
intro. apply H. right. assumption. Qed.

ひとこと: 含意と論理積の右分配則は Classical をインポートしないと tauto で証明できません。古典論理を使えば上記のように証明できます。

2-4. 形式化された推論

モーダスポネンス（三段論法）や対偶証明などの推論は、演繹定理を使うことでトートロジーとしても表せます。これらを証明してみます:

• $P \land (P \to Q) \to Q$ (三段論法に相当)
• $(\lnot Q \to \lnot P) \to P \to Q$ (対偶証明に相当) ＜古典論理＞
• $(P\to Q)\land(Q\land R\to S)\to(P\land R\to S)$ (カットに相当)

Goal P /\ (P -> Q) -> Q.
intros. destruct H as [H1 H2]. apply H2. assumption. Qed.

Goal (~Q -> ~P) -> P -> Q.
intros H H1. apply imply_to_or in H. destruct H. apply NNPP. assumption. contradiction. Qed.

Goal (P -> Q) /\ (Q /\ R -> S) -> (P /\ R -> S).
intros H1 H2. destruct H1 as [H3 H4]. destruct H2.
apply H4. split. apply H3. assumption. assumption. Qed. 

ひとこと: よく知られているように対偶証明は古典論理でしか成立しないことがわかります。

2-5. ヒルベルト流

ヒルベルト流の証明系で使われる公理を証明してみます(Rautenbergの教科書から持ってきました):

• $(P\to Q \to R) \to (P\to Q)\to P\to R$
• $P\to Q \to P\land Q$
• $P\land Q \to P$
• $(P\to\lnot Q)\to Q\to\lnot P$ ＜古典論理＞

Goal (P -> Q -> R) -> (P -> Q) -> P -> R.
intros. apply H. exact H1. apply H0. exact H1. Qed.

Goal P -> Q -> P /\ Q.
intros. split. assumption. assumption. Qed.

Goal P /\ Q -> P.
intros. destruct H. assumption. Qed.

Goal (P -> ~Q) -> Q -> ~P.
intros. apply imply_to_or in H. destruct H. assumption. contradiction. Qed.

ひとこと: ヒルベルト流の証明系の公理が証明でき、ヒルベルト流の推論規則がビルトインされているということは、Coqの証明能力はヒルベルト流と同等かそれ以上であることがわかります。

2-6. ややこしい奴ら

古典論理でしか証明できない定理を整理し証明します。

• $P\lor \lnot P$ : 排中律
• $P\lor (P\to Q)$ : 一般化された排中律
• $(P\to Q)\land(\lnot P \to Q)\to Q$ : 場合分け推論
• $\lnot\lnot P \to P$ : 二重否定除去
• $((P \to Q) \to P) \to P$ : パースの法則
• $(\lnot P \to \bot)\to P$ :否定型の背理法
• $\lnot(P\land Q) \to(\lnot P\lor \lnot Q)$ :ドモルガン則の1つ

Goal P \/ ~P.
apply classic. Qed.

Goal P \/ (P -> Q).
destruct (classic P). left. assumption. right. intro. contradiction. Qed.

Goal (P->Q) /\ (~P->Q) -> Q.
intros H. destruct H as [H1 H2]. destruct (classic P).
apply H1. assumption. apply H2. assumption. Qed.

Goal ~~P -> P.
intros. apply NNPP. assumption. Qed.

Goal ((P -> Q) -> P) -> P.
intros H. apply imply_to_or in H. destruct H.
apply not_imply_elim in H. assumption. assumption. Qed.

Goal (~P -> False) -> P.
intro H. apply imply_to_or in H. destruct H. apply NNPP. assumption. contradiction. Qed.

Goal ~(P /\ Q) -> ~P \/ ~Q.
intros. apply not_and_or in H. assumption. Qed.

3. おわりに

お勧めする参考書があれば教えてくれるとうれしいです。数学方面よりも 様相論理 関連に興味があります。