ハフマン符号を実装してみた（JavaScript）

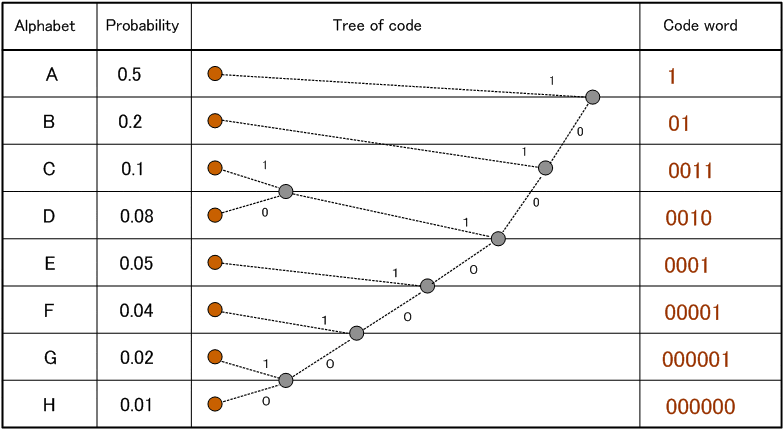
勉強したので習作。計算効率は完全に無視。

1. 概念理解

解きたい課題: N種類の値を取りうる事象があり、それぞれの値が生成される確率（≒頻度）がわかっている。できるだけ圧縮効率をあげて 0/1で構成されるビット列にエンコード/デコードしたい。

具体例1: サイコロを何度も振る。6種類の値がありえて、それぞれの値が生成される確率がわかっている（どの値も同じ頻度 1で生成される）。できるだけ圧縮効率を上げてサイコロ目を出た順にビット列にエンコード・デコードしたい。

具体例2: 野鳥観察。一匹ずつ鳥が横切る。鳥の種類は 4種類。それぞれの鳥がくる頻度がわかっている(スズメは10, ハトが5, ツバメが2, カラスが 1) 。できるだけ圧縮効率を上げて鳥が来た順序をビット列にエンコード・デコードしたい。

イメージ図:

ABAACBBAC --- [エンコーダ] ---> 010010010111000111000111 --- [デコーダ] ---> ABAACBBAC

2. FAQ

ビット列のどこで区切るの？区切り文字みたいのあるの？: ハフマン符号では区切り文字はない。なくてもどこで区切ればよいのかわかる（ように作る）。

ハフマン符号のアルゴリズムは一種類なの？: 事前に必要となる統計値（＝頻度分布）が一緒なら、誰が作っても同じ圧縮効率になる。ただ、どのようなビット列になるかには任意性がある（実装の際に詳細を言及する）。

ハフマン符号より高圧縮にできないの？: 「1事象ごとにビット列に変換する」という枠組みではハフマン符号が最高圧縮。ただ、「N事象ごとにビット列に変換する」という より柔軟な枠組みで考えればもっと圧縮できる。

3. ハフマン木を作る

最初の一歩は、頻度を入力としてハフマン木を作ること。以下の図がわかりやすい。「頻度が一番小さい二つの事象をまとめて一つの木にする（その木の頻度は二つの頻度の和）」という手順を、全部が一つの木になるまで続ける。

出典: http://www.mnc.toho-u.ac.jp/v-lab/yobology/Huffman_code/Huffman_code.htm

木構造を配列で表現する方向で素直にコードに落とすとこうなった:

const DATA = [
  ['A', 50],
  ['B', 20],
  ['C', 10],
  ['D', 8],
  ['E', 5],
  ['F', 4],
  ['G', 2],
  ['H', 1],
];

function treeOf (stats) {
  const arr = stats.map(x => [...x]); // copy
  while (arr.length !== 1) {
    arr.sort((a, b) => a[1] < b[1]); // by freq
    const [a, b] = arr.splice(-2); // pop 2 nodes
    arr.push([[a[0], b[0]], a[1] + b[1]]); // push 1 node
  }
  return arr[0][0];
}

console.log(JSON.stringify(treeOf(DATA)));
// -> ["A",[[["C","D"],[["F",["G","H"]],"E"]],"B"]]

4. エンコーダを作る

木を作れば、先ほどの図のように各事象に対応するビット列が得られる。これを連想記憶（ハッシュテーブル）で保持しておきたい。

木の左側（私の実装では配列の0番目の要素）に行くときには 0 を割り当て、木の右側（私の実装では配列の1番目の要素）に行くときには 1 を割り当てる。再帰的に木を下っていき、末端に突き当たったら（私の実装では string に突き当たったら）、その事象の符号語がわかる。

function dictOf(tree) {
  const result = {};
  const rfn = (obj, ctx) => {
    if (typeof obj === 'string') {
      result[obj] = ctx;
      return;
    }
    rfn(obj[0], ctx + '0');
    rfn(obj[1], ctx + '1');
  };
  rfn(tree, '');
  return result;
}

console.log(dictOf(treeOf(DATA)));
/* output
{ A: '0',
  C: '1000',
  D: '1001',
  F: '10100',
  G: '101010',
  H: '101011',
  E: '1011',
  B: '11' }
*/

木の構造がちょっと違う（トポロジー的には同じ）ので、上記の図とは違う形でエンコードされる。

使いやすいように仕上げておく:

const encoder = dict => ids => ids.map(id => dict[id]).join('');

const encode = encoder(dictOf(treeOf(DATA)));
console.log(encode(['A', 'B', 'C'])); // -> 0111000

5. デコーダをつくる

デコーダは、ストリームから 1ビットずつ読み込んでいき、それが 0 なら木の左側に行き、それが 1 なら木の右側に行く。行った先が末端だったら、その場所にある事象が復号される。行った先が末端でない場合は、まだ復号できないので次の 1ビットを読み込んで、以下同様。

素直に実装するとこんな感じになった:

const decoder = tree => bits => {
  let current = tree;
  // define 1-bit decoder
  const _decode = bit => {
    current = bit === '0' ? current[0] : current[1];
    if (typeof current === 'string') { // decoded!
      const result = current;
      current = tree;
      return result;
    }
    return null; // needs more to decode
  };
  // do the work
  const result = [];
  for (const bit of bits) {
    const val = _decode(bit);
    if (val) {
      result.push(val);
    }
  }
  return result;
};

const tree = treeOf(DATA);
const decode = decoder(tree);
console.log(decode('0111000')); // -> [ 'A', 'B', 'C' ]

6. 遊んでみる

エンコーダとデコーダを再掲

const tree = treeOf(DATA);
const encode = encoder(dictOf(tree));
const decode = decoder(tree);

まずは全ての事象が符号化できることを確認:

console.log(encode([...'ABCDEFGH']))
// 以下の出力だが、スペースは手動でいれた
// 0 11 1000 1001 1011 10100 101010 101011

符号化して復号して元に戻ることを確認:

console.log(decode(encode([...'ABCDEFGH'])).join(''));
// -> 'ABCDEFGH'
console.log(decode(encode([...'AHBBCEFAC'])).join(''));
// -> AHBBCEFAC

10000事象をエンコードして平均ビット長を確認:

const observe = num => {
  const result = [];
  [...Array(num).keys()].forEach(() => { // num times
    const rval = Math.random();
    const total = DATA.reduce((a, x) => a + x[1], 0);
    let acc = 0;
    for (const [id, freq] of DATA) {
      acc += freq / total;
      if (acc > rval) {
        result.push(id);
        return;
      }
    }
  });
  return result;
};

const input = observe(10000);
const stats = {}
input.forEach(x => stats[x] = (stats[x] || 0) + 1);
console.log(stats)
console.log(encode(input).length / 10000);

/*output
{ A: 5009, B: 2034, D: 819, C: 998, E: 494, G: 177, H: 101, F: 368 }
2.1829
*/

平均ビット長は 2.18 だが、これは期待値 2.2 と同程度。情報源のエントロピーを計算してみる

const total = DATA.reduce((a, x) => a + x[1], 0);
console.log(DATA.reduce((a, x) => a + (x[1]/total * (Math.log2(x[1]/total))), 0));
// -> 2.1692

理論限界との比較:

const dict = dictOf(tree);
const total = DATA.reduce((a, x) => a + x[1], 0);
const entoropy = DATA.reduce((a, x) => a + (x[1]/total * (-Math.log2(x[1]/total))), 0);
const average = DATA.reduce((a, x) => a + x[1]/total * dict[x[0]].length, 0);

console.log(entoropy, average, average / entoropy * 100);
// -> 2.1692532616767854 2.2 101.41738813380638

この事例でのハフマン符号は、理論限界よりも 1.4 % だけ平均ビット長が長くなるということ。ほとんど最適といっていい。