はじめに
基本情報技術者試験の学習中なので、学んだことをメモします
誤り等ございましたらご教示いただけますと幸いです🙇
n進数
n進数とは、1桁の数をn個の記号で数値を表現する方法のことです。
n進数の足し算
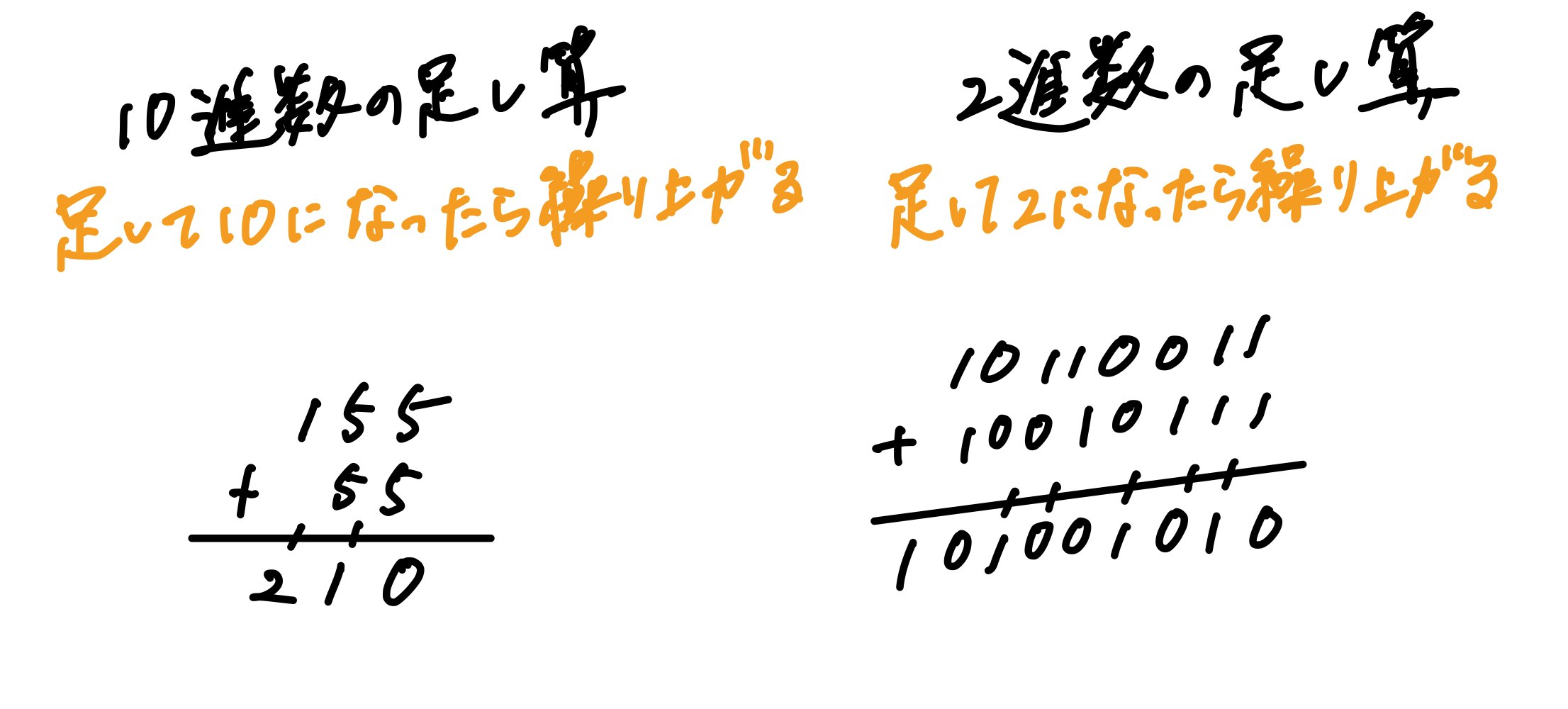
n進数の引き算
コンピューターは引き算ができない為、負の数の足し算を行う
負の数はnの補数で表現することができる
補数

2進数で2の補数を表現
2進数2の補数を利用して引き算

符号ビット
-(マイナス)を表現する場合に、符号ビットを利用することがあります。
先頭ビットを符号ビットとして代用します。
見た目では符号ビットを利用しているかわからないため、
利用している場合は、「符号ビットを利用している旨の」前置きが必ずあります。
1:負の数
0:正の数
シフト演算
2進数を表すビット列を左右にずらすこと
10進数の場合
615 左にずらす(*10)← 61.5 →右にずらす(*1/10) 6.15
桁がズレると10倍となる(基数)
2進数の場合
10進数と同様、左にn個ズレると元の数値の2ⁿ倍になる
右にn個ズレると下の数値の2⁻ⁿ倍になる
桁をズラすシフト演算は、論理シフトと算術シフトがある
論理シフト(左シフト:かけ算)
符号を考慮せずに単純に桁をずらすことを論理シフトという
論理シフトのやり方は、nビット左シフトし、溢れた数値は無視、空いたスペースに0を格納します
例)8ビット2進数の数値を左に2ビット論理シフトする
8ビットで表せる範囲の数値は計算できない!
272になるはずが、16になってしまいました。。
これは、8ビットで表せる0~255を超えてしまっているからです!
こういった現象をオーバーフローと言います
論理シフト(右シフト:割り算)
例)8ビット2進数の数値を右に2ビット論理シフトする
算術シフト(左シフト:かけ算)
算術シフトでは、符号付き8ビット2進数で表せる-128~127を超えると
論理シフト同様オーバーフローを起こします
算術シフト(右シフト:割り算)
論理シフト・算術シフトまとめ
| 論理シフト(符号を考慮しない) | 算術シフト(符号を考慮する) | |
|---|---|---|
| 左シフト(かけ算) | ・空いたスペースに0を入れる ・1がはみ出るとオーバーフロー |
・空いたスペースに0を入れる ・符号ビットと異なる数字がはみ出るとオーバーフロー |
| 右シフト (割り算) | ・空いたスペースに0を入れる ・はみ出た分は割り算の余り |
・空いたスペースに符号ビットを入れる ・はみ出た分は割り算の余り |






