この記事の前の話はこちら
この記事の続きはこちら
サイクロイド振り子
単振り子をやったので、次にサイクロイド振り子をやってみた。
一様重力場の中で、1個の質点が鉛直面内でサイクロイド曲線の軌道上に束縛されながら自由に運動する系。
単振り子では「振り子の等時性」が成り立たないのであったが、サイクロイド振り子では厳密に成り立つことが知られている。
果たして本当にそうなるのだろうか。
結果を楽しみにしながら、やってみた。
理屈
運動方程式
サイクロイド軌道のある鉛直面内に、鉛直上向きの$z$軸と水平方向の$x$軸をとる。
軌道は、媒介変数 $\theta$ と 定数 $L$ を用いて
$$
x = L \hspace{0.1em} ( \hspace{0.1em} \theta + \sin \theta \hspace{0.1em} )
$$
$$
z = - L \hspace{0.1em} \cos \theta
$$
で表されるとする。
質点には、その位置・速度によらず、一定の方向(鉛直下向き)に一定の 大きさ $m \hspace{0.1em} g$ ( $m$ : 質点の質量、 $g$ : 重力加速度の大きさ)の重力がはたらく。
サイクロイド振り子の運動方程式は、Lagrange形式で記述すれば簡単に得られるのだが、敢えてここではNewton形式で行く。
この重力場の中で質点がサイクロイド軌道上を自由に運動するとき、質点が受ける力は、重力と運動をサイクロイド軌道上に束縛するための束縛力の2つである。
束縛力は必ず軌道に垂直な方向にはたらく。
その方向の束縛力を $R$ とおく。
$R$ は軌道より上に向かう向きを正とする。
振り子の運動方程式は、
質点の位置における $\displaystyle \frac{dz}{dx}$ を $\tan \phi$ とおく(つまり、 $\phi$ は軌道の接線が水平面となす角で、 $\displaystyle - \frac{\pi}{2} \leq \phi \leq \frac{\pi}{2}$ を満たす)と
$$
m \hspace{0.1em} \ddot{x} = - R \hspace{0.1em} \sin \phi
$$
$$
m \hspace{0.1em} \ddot{z} = R \hspace{0.1em} \cos \phi - m \hspace{0.1em} g
$$
$$
\tan \phi = \frac{dz}{dx}
$$
である。
この方程式を解いて $x \hspace{0.1em} , \hspace{0.1em} z$ を $t$ の関数として求めるには、 $R$ を既知の量で表さなければならない。
$R$ は、この運動方程式の解が「与えられた軌道上を進む」という解にならなければならない、という条件により定まる。
つまり、与えられた軌道の式とそれより導かれる式を用いれば、運動方程式を解くことができるはずだ。
与えられた軌道の式より導かれる式とは
$$
\dot{x} = L \hspace{0.1em} \dot{\theta} \hspace{0.1em} ( \hspace{0.1em} 1 + \cos \theta \hspace{0.1em} )
$$
$$
\dot{z} = L \hspace{0.1em} \dot{\theta} \hspace{0.1em} \sin \theta
$$
$$
\ddot{x} = L \hspace{0.1em} \left( \hspace{0.1em} \ddot{\theta} \hspace{0.1em} ( \hspace{0.1em} 1 + \cos \theta \hspace{0.1em} ) - \dot{\theta}^{2} \hspace{0.1em} \sin \theta \hspace{0.1em} \right)
$$
$$
\ddot{z} = L \hspace{0.1em} \left( \hspace{0.1em} \ddot{\theta} \hspace{0.1em} \sin \theta + \dot{\theta}^{2} \hspace{0.1em} \cos \theta \hspace{0.1em} \right)
$$
の4本である。
ここまでに書いた9本の式をすべてまとめて、連立方程式とみなす。
すると、 $\dot{x} \hspace{0.1em} , \hspace{0.1em} \dot{z}$ を既知として
$$
\phi = \frac{\theta}{2}
$$
$$
\theta = 2 \hspace{0.1em} \tan^{-1} \frac{\dot{z}}{\dot{x}}
$$
$$
\dot{\theta} = \frac{\dot{z}}{L \hspace{0.1em} \sin \theta}
$$
$$
R = m \hspace{0.1em} \left( \hspace{0.1em} L \hspace{0.1em} \dot{\theta}^{2} + g \hspace{0.1em} \right) \hspace{0.1em} \cos \frac{\theta}{2}
$$
$$
\ddot{x} = - \frac{1}{2} \hspace{0.1em} \left( \hspace{0.1em} L \hspace{0.1em} \dot{\theta}^{2} + g \hspace{0.1em} \right) \hspace{0.1em} \sin \theta
$$
$$
\ddot{z} = \frac{1}{2} \hspace{0.1em} \left( \hspace{0.1em} L \hspace{0.1em} \dot{\theta}^{2} + g \hspace{0.1em} \right) \hspace{0.1em} ( \hspace{0.1em} 1 + \cos \theta \hspace{0.1em} ) - g
$$
が得られる。
この最後の2本の式が運動方程式を既知の量だけで書いたものになっているので、これを解けばよい。
(ちなみに、この他に $x \hspace{0.1em} , \hspace{0.1em} z \hspace{0.1em} , \hspace{0.1em} \ddot{\theta}$ を $\dot{x} \hspace{0.1em} , \hspace{0.1em} \dot{z}$ で表す式も得られるので、9本の方程式から解ける未知数の数は9個であり、ちゃんと9元連立方程式になっている。)
プログラム
運動方程式の関数 f
f <- function(f.t,f.rv) {
f.theta <- 2.0 * atan( f.rv$vz / f.rv$vx )
f.theta[which( f.rv$vx == 0 )] = acos( - ( z0 + v0^2 / ( 2.0 * g ) ) / L ) * sign( f.rv$x )
f.thetadot <- f.rv$vz / ( L * sin( f.theta ) )
f.ax <- - ( L * f.thetadot^2 + g ) * sin( f.theta ) / 2.0
f.az <- ( L * f.thetadot^2 + g ) * ( 1.0 + cos( f.theta ) ) / 2.0 - g
return( data.frame( x=f.rv$vx , y=f.rv$vy , z=f.rv$vz , vx=f.ax , vy=0.0 , vz=f.az ) )
}
4行目の f.theta[which( f.rv$vx == 0 )] = acos( - ( z0 + v0^2 / ( 2.0 * g ) ) / L ) * sign( f.rv$x ) は、 $\dot{x} = 0$ の場合に限り $\displaystyle \theta = 2 \hspace{0.1em} \tan^{-1} \frac{\dot{z}}{\dot{x}}$ を計算できないことへの対応。
$\dot{x} = 0$ となるのは振り子の速度が 0 になるときだけなので、そのときの $z$ を力学的エネルギー保存則で求め、 $z = - L \hspace{0.1em} \cos \theta$ を使って $\theta$ を求めている( z0 : 初期位置の $z$ , v0 : 初速度の大きさ)。
$z$ の値は f.rv$z に格納されているので、わざわざそんな方法で求める必要は、本当は、ない。
しかし、 f.theta[which( f.rv$vx == 0 )] = acos( -f.rv$z / L ) * sign( f.rv$x ) とプログラムすると、実行時に
警告メッセージ:
acos(-f.rv$z/L) で: 計算結果が NaN になりました
なる警告が出る。(ただし計算結果は問題なく正しい。)
どうやら、 which( f.rv$vx == 0 ) の条件を満たす要素が f.rv$vx に無い場合でも右辺の値は計算されているらしく、振り子が最下点にきた瞬間あたりで f.rv$z の絶対値が計算機の誤差のせいで $L$ よりもわずかに大きくなってしまう(本来なら最下点で $z = - L$ となるはず)ことによる acos の「値なし」を教えてくれているようだ。
実際にはその NaN はどこにも代入されないので、計算結果に影響は与えないため、この警告が出ても特に害はない。
が、なんとなく気持ち悪いので、警告を出さない方法としてここでは $z$ を z0 + v0^2 / ( 2.0 * g ) で与えることにしたのである。
いちおう、理論上も、こうすることで「 $\dot{x} \hspace{0.1em} , \hspace{0.1em} \dot{z}$ から他のすべての量を求める」という方針にちゃんと沿っていることになり、筋が通っている(と思う)。
境界条件の関数 boundary.condition
境界条件は、とくにない。
運動がサイクロイド軌道上に束縛されているという束縛条件は、運動方程式を定式化するときに考慮したので、運動方程式にすでに含まれている。
boundary.condition <- function(boundary.condition.t,boundary.condition.rv) {
return( boundary.condition.rv )
}
パラメータ
n <- 1
g <- 9.8
L <- 1.0
m <- c( 1.0 )
t0 <- 0.0
theta0 <- 90.0 / 180.0 * pi
v0 <- 0.0
x0 <- L * ( theta0 + sin( theta0 ) )
y0 <- 0.0
z0 <- - L * cos( theta0 )
vx0 <- v0 * cos( theta0 / 2.0 )
vy0 <- 0.0
vz0 <- v0 * sin( theta0 / 2.0 )
tend <- 10.0
Deltat <- 2.0e-4
draw.step <- 100
xmin <- - L * 2.6
xmax <- L * 2.6
ymin <- - L
ymax <- L
n : 質点数 今回は 1
g : 重力加速度の大きさ $g$
L : $L$
m : 質点の質量 $m$
t0 : 初期状態の時刻
theta0 : 初期状態での $\theta$
v0 : 初期状態での質点の速度の大きさ
x0 y0 z0 : 初期状態での質点の座標
vx0 vy0 vz0 : 初期状態での質点の速度の各成分
tend : 終状態の時刻
結果を出力するコード
前回(単振り子)と同じ。
全リスト
################################################################
## parameters
## modify this section to change condition
################################################################
n <- 1
g <- 9.8
L <- 1.0
m <- c( 1.0 )
t0 <- 0.0
theta0 <- 90.0 / 180.0 * pi
v0 <- 0.0
x0 <- L * ( theta0 + sin( theta0 ) )
y0 <- 0.0
z0 <- - L * cos( theta0 )
vx0 <- v0 * cos( theta0 / 2.0 )
vy0 <- 0.0
vz0 <- v0 * sin( theta0 / 2.0 )
tend <- 10.0
Deltat <- 2.0e-4
draw.step <- 100
xmin <- - L * 2.6
xmax <- L * 2.6
ymin <- - L
ymax <- L
################################################################
## output
## modify this section to change the method to output
################################################################
output <- function() {
plot(rv$x,rv$z,xlim=c(xmin,xmax),ylim=c(ymin,ymax),xlab="x",ylab="z",tcl=0.5,las=1,mgp=c(2.5,0.3,0),text(0.5,0.8,labels=paste("t =",as.character(round(t,digits=3)))))
output.e <- m / 2.0 * ( rv$vx^2 + rv$vy^2 + rv$vz^2 ) + m * g * rv$z
return( rbind( results , c( t , rv$x , rv$z , output.e ) ) )
}
################################################################
## models
## modify this section to change physical model
################################################################
f <- function(f.t,f.rv) {
f.theta <- 2.0 * atan( f.rv$vz / f.rv$vx )
f.theta[which( f.rv$vx == 0 )] = acos( - ( z0 + v0^2 / ( 2.0 * g ) ) / L ) * sign( f.rv$x )
f.thetadot <- f.rv$vz / ( L * sin( f.theta ) )
f.ax <- - ( L * f.thetadot^2 + g ) * sin( f.theta ) / 2.0
f.az <- ( L * f.thetadot^2 + g ) * ( 1.0 + cos( f.theta ) ) / 2.0 - g
return( data.frame( x=f.rv$vx , y=f.rv$vy , z=f.rv$vz , vx=f.ax , vy=0.0 , vz=f.az ) )
}
boundary.condition <- function(boundary.condition.t,boundary.condition.rv) {
return( boundary.condition.rv )
}
################################################################
## engines
## do not modify this section
################################################################
runge.kutta.4th <- function(runge.kutta.4th.t,runge.kutta.4th.rv) {
runge.kutta.4th.k0 <- f( runge.kutta.4th.t , runge.kutta.4th.rv ) * Deltat
runge.kutta.4th.k1 <- f( runge.kutta.4th.t + Deltat / 2.0 , runge.kutta.4th.rv + runge.kutta.4th.k0 / 2.0 ) * Deltat
runge.kutta.4th.k2 <- f( runge.kutta.4th.t + Deltat / 2.0 , runge.kutta.4th.rv + runge.kutta.4th.k1 / 2.0 ) * Deltat
runge.kutta.4th.k3 <- f( runge.kutta.4th.t + Deltat , runge.kutta.4th.rv + runge.kutta.4th.k2 ) * Deltat
runge.kutta.4th.Deltarv <- ( runge.kutta.4th.k0 + 2.0 * ( runge.kutta.4th.k1 + runge.kutta.4th.k2 ) + runge.kutta.4th.k3 ) / 6.0
return( runge.kutta.4th.rv + runge.kutta.4th.Deltarv )
}
### preparation to output
png(filename="%04d.png",width=960,height=960,units="px",res=192)
results <- matrix( c( 0 , 0 , 0 , 0 ) , nrow=1 , ncol=4 )
colnames(results) <- c( "t" , "x" , "z" , "E" )
###
t <- t0
rv <- data.frame( x=x0 , y=y0 , z=z0 , vx=vx0 , vy=vy0 , vz=vz0 )
while(t<=tend) {
results <- output()
for(i in 1:draw.step) {
rv <- runge.kutta.4th(t,rv)
rv <- boundary.condition(t,rv)
t <- t + Deltat
}
}
### post-processing to output
graphics.off()
write.table(as.data.frame(results[-1,]),file="results",sep=" ",row.names=FALSE,col.names=TRUE)
###
実行結果
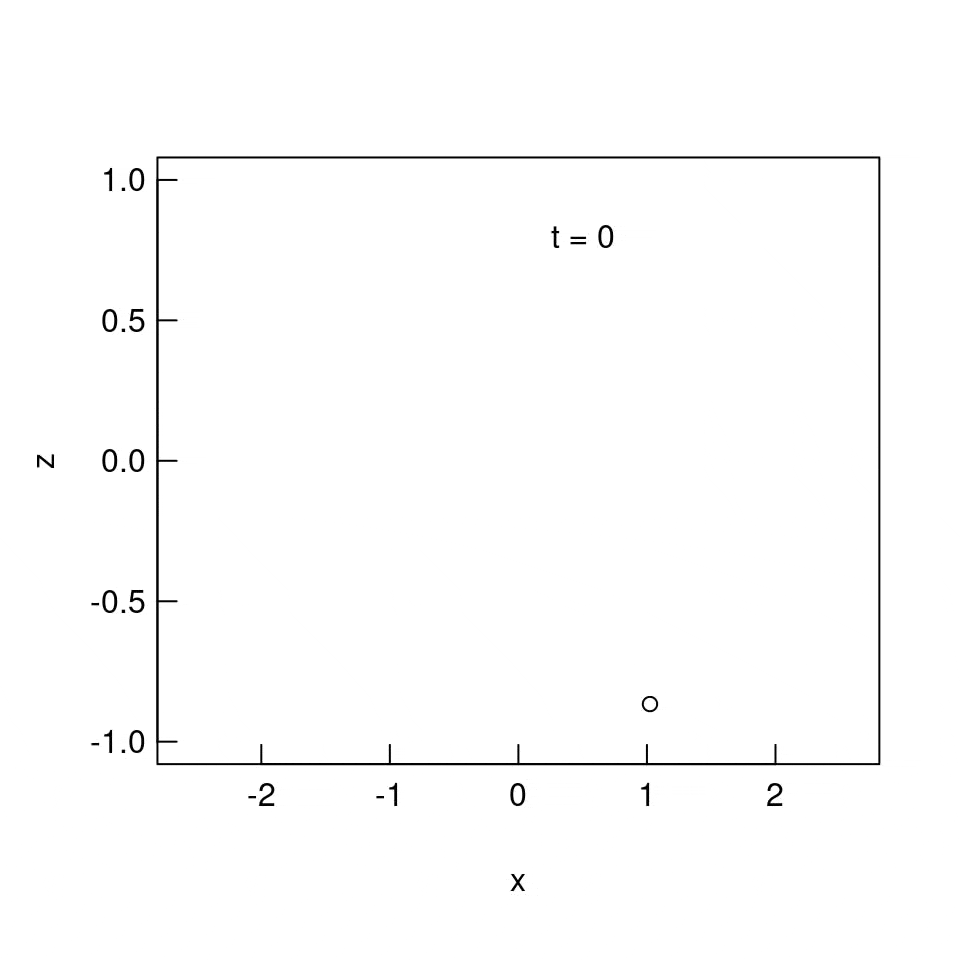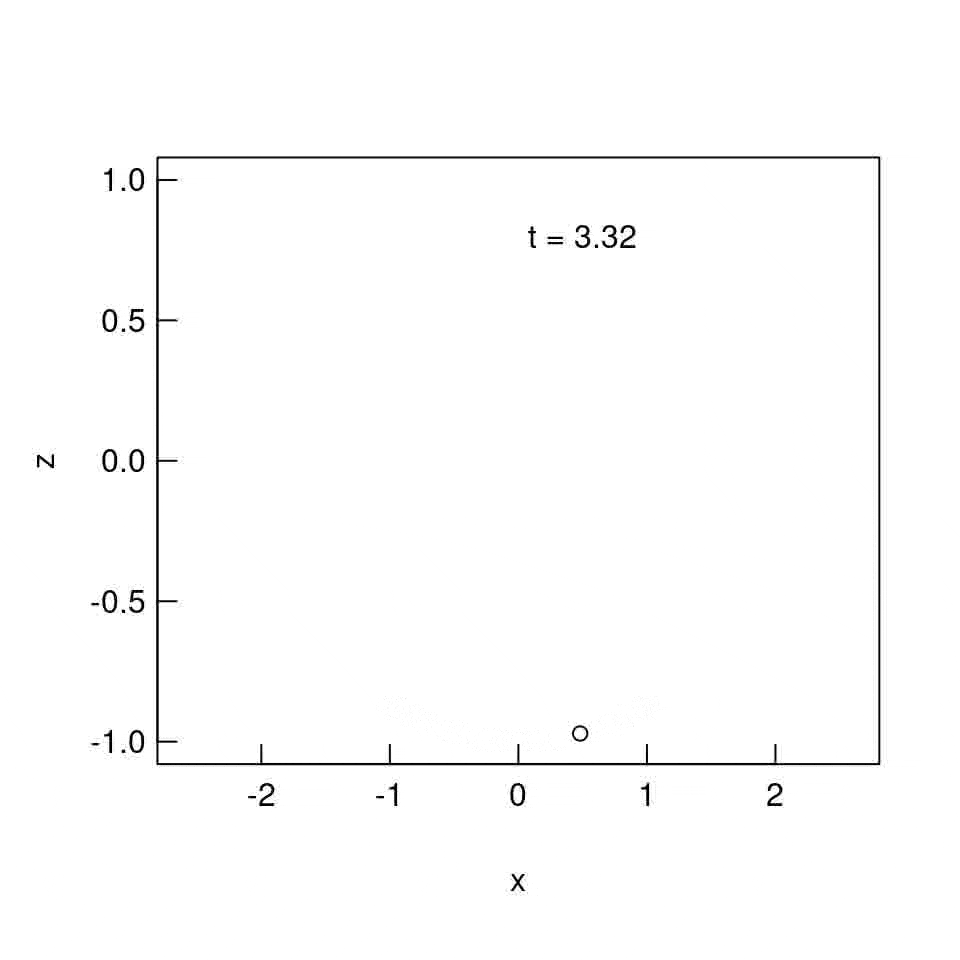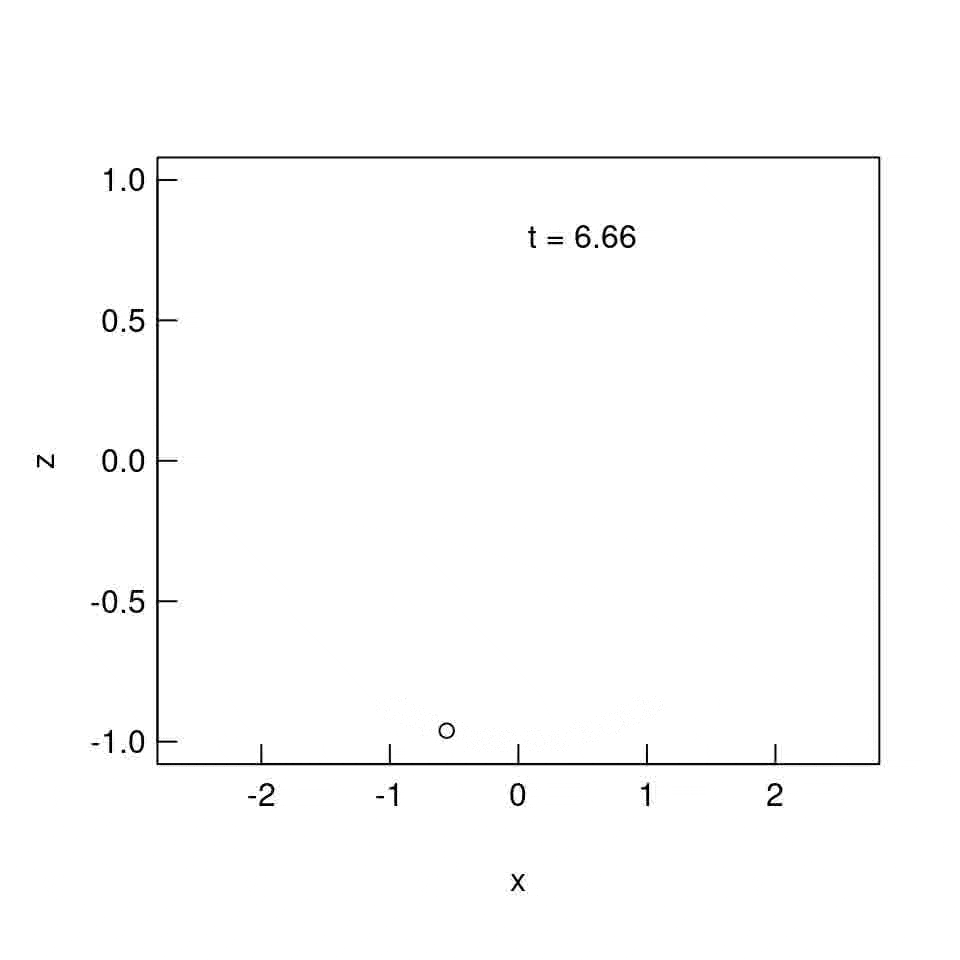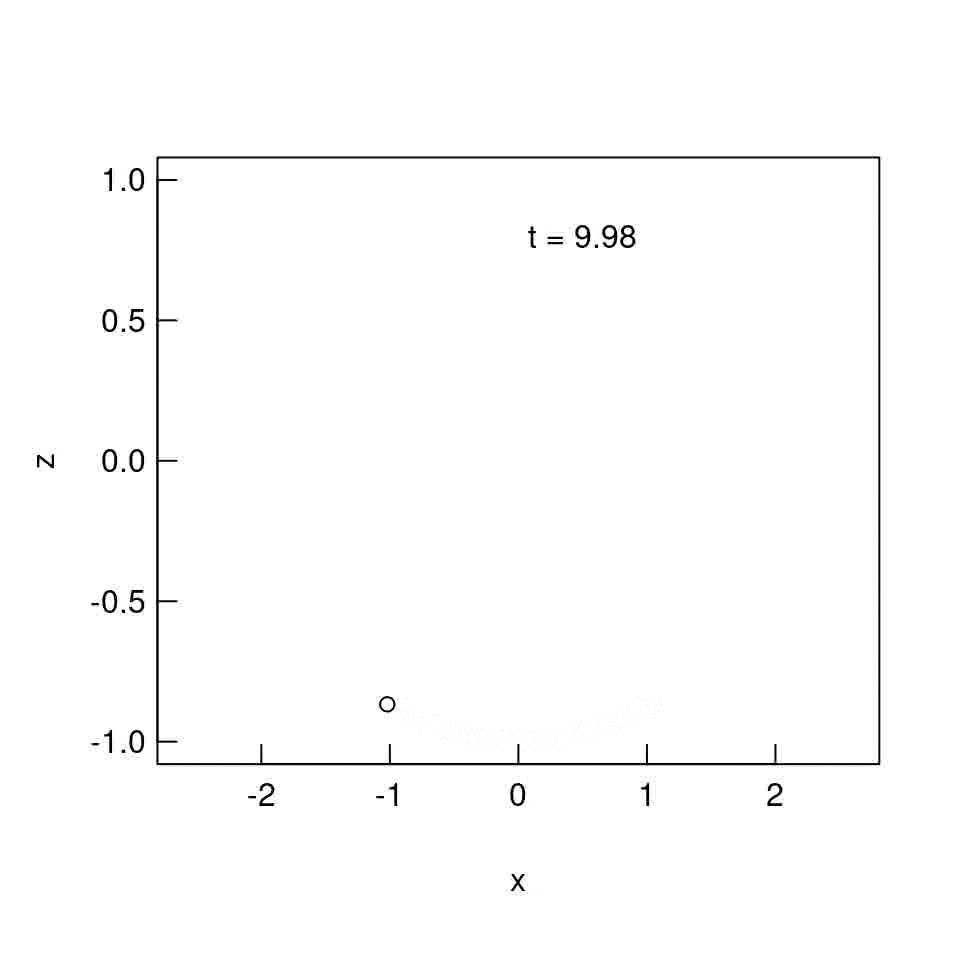
$\theta_{0} = 90^{\circ}$ の場合
$\theta_{0} = 60^{\circ}$ の場合
$\theta_{0} = 30^{\circ}$ の場合
$\theta_{0} = 5^{\circ}$ の場合
数値出力をチェック
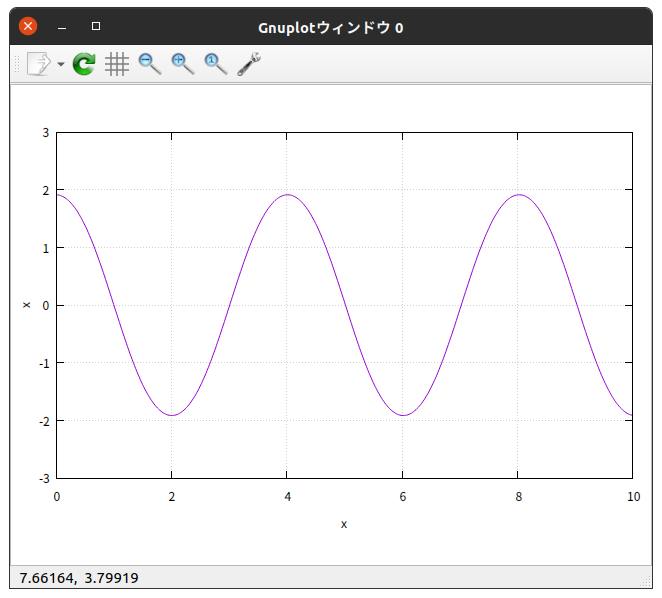
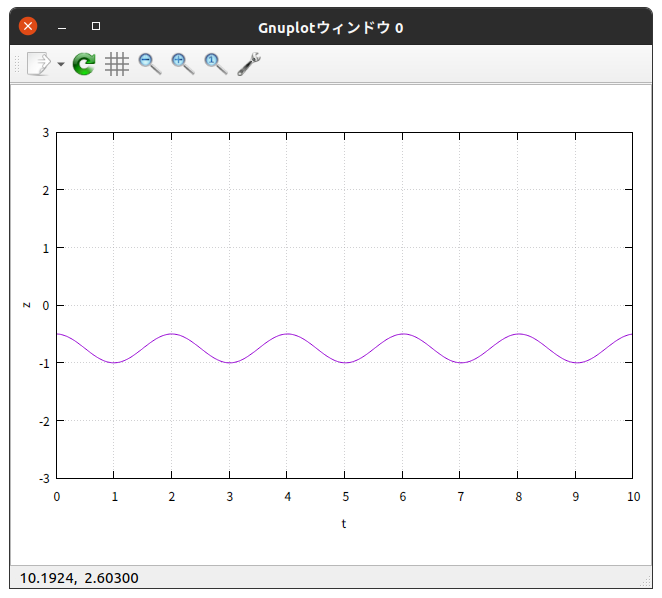
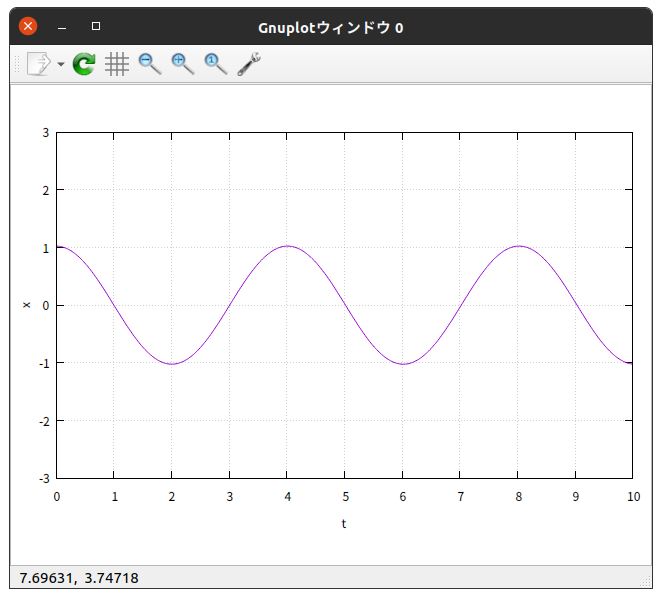
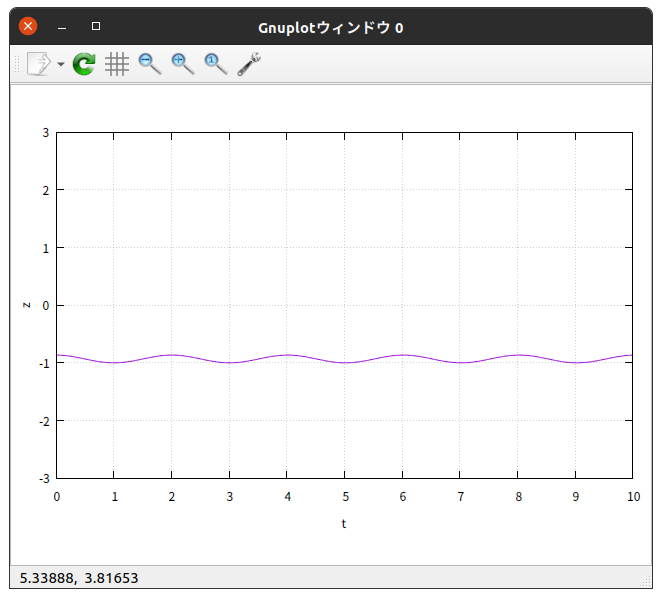
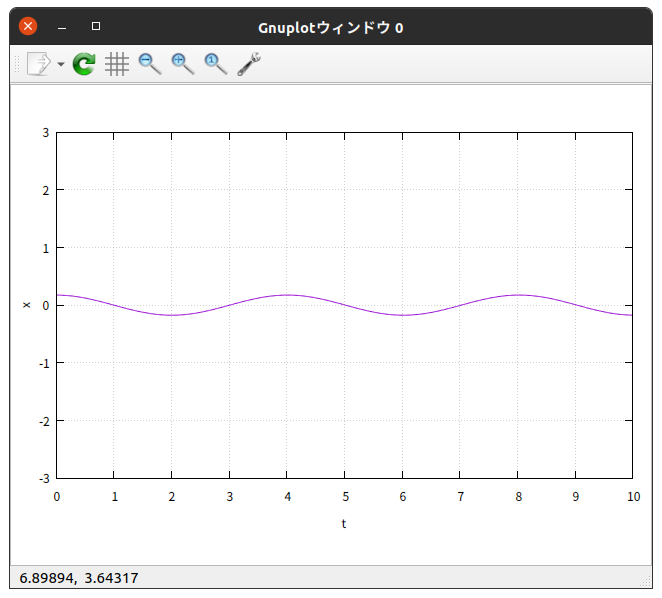
$\theta_{0} = 90^{\circ}$ の結果を、 gnuplot を使って $x$-$t$ グラフと $z$-$t$ グラフに描いてみると
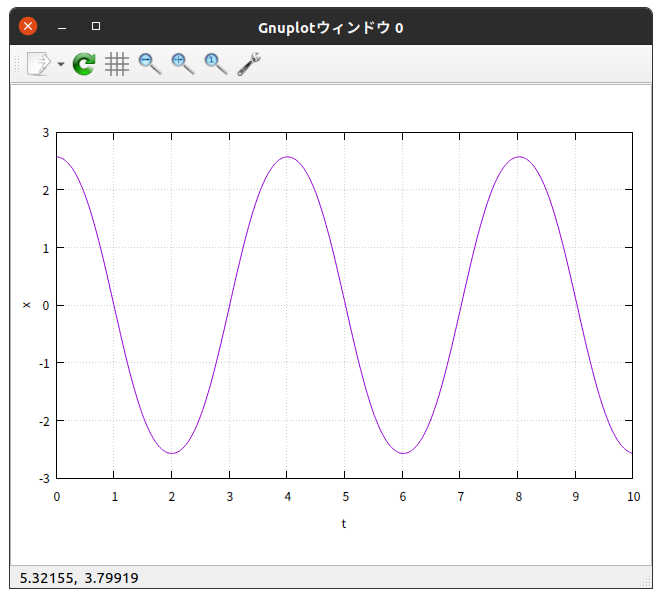
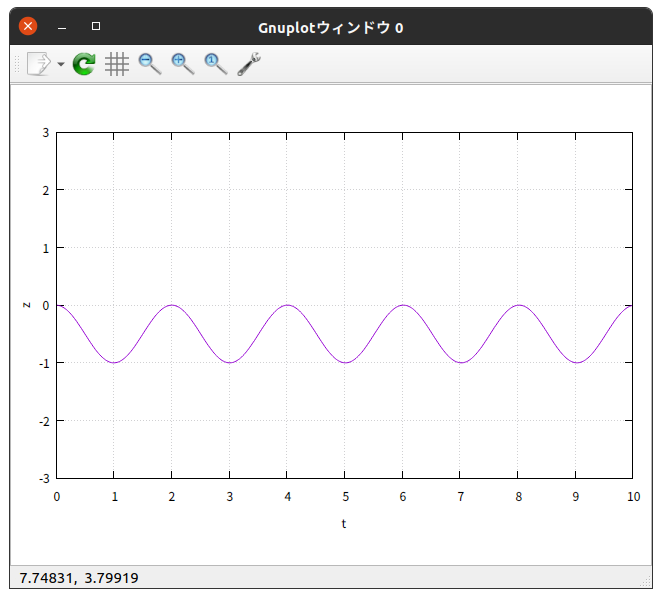
綺麗に振動している。
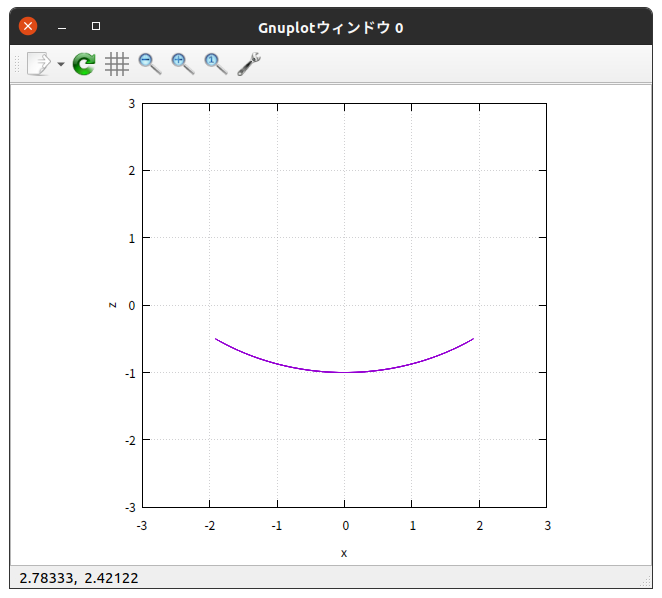
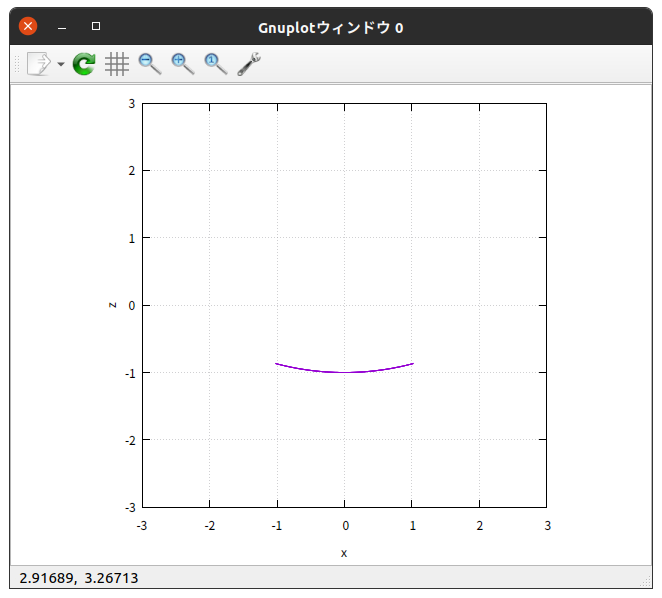
$z$-$x$ グラフにしてみると
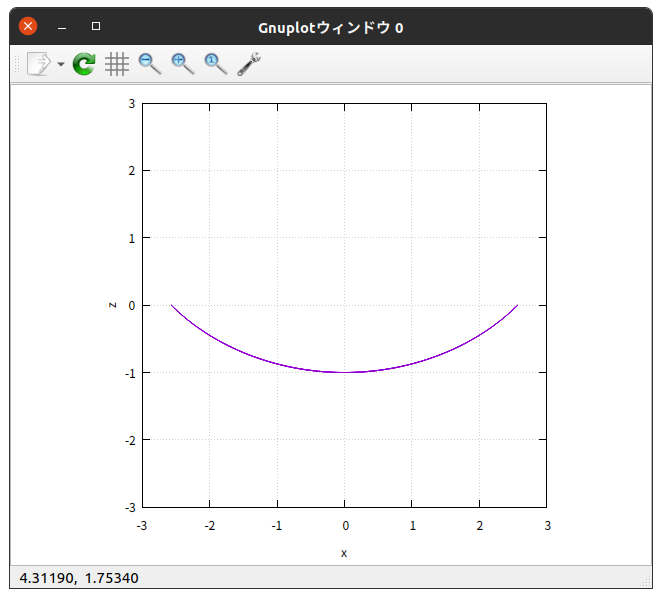
サイクロイド軌道を描いている。
(パッと見ただけではわからないが。笑)
$\theta_{0} = 60^{\circ}$ の場合の結果は、以下の通り。
$\theta_{0} = 30^{\circ}$ の場合の結果は、以下の通り。
$\theta_{0} = 5^{\circ}$ の場合の結果は、以下の通り。
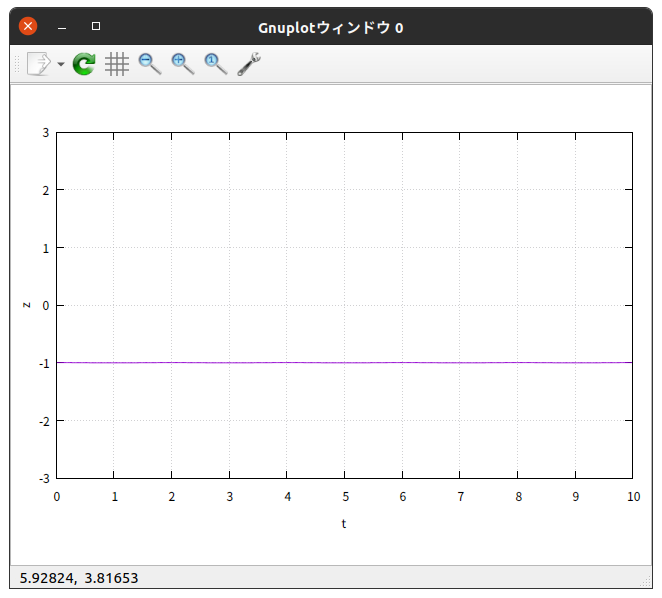
力学的エネルギーの保存
縦軸に 力学的エネルギー $E$ 、横軸に 時刻 $t$ をとってグラフに描いた。
$\theta_{0} = 90^{\circ}$ の場合では
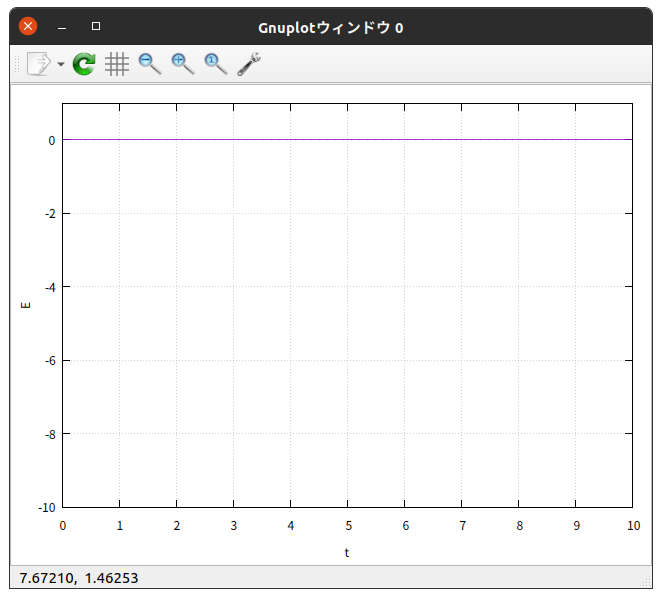
となった。力学的エネルギーは保存しているようである。
$\theta_{0} = 60^{\circ}$ の場合では
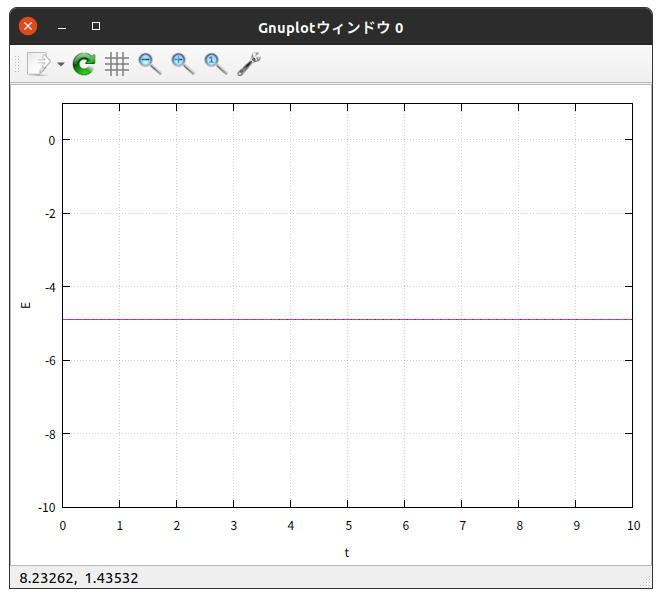
$\theta_{0} = 30^{\circ}$ の場合では
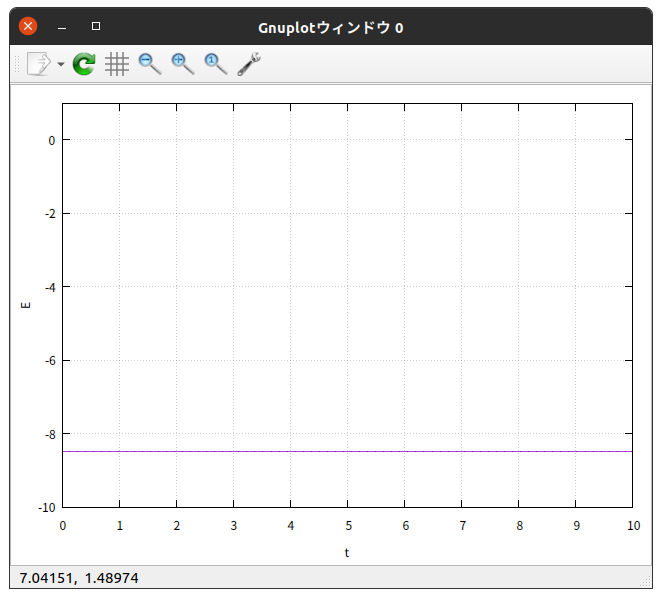
$\theta_{0} = 5^{\circ}$ の場合では
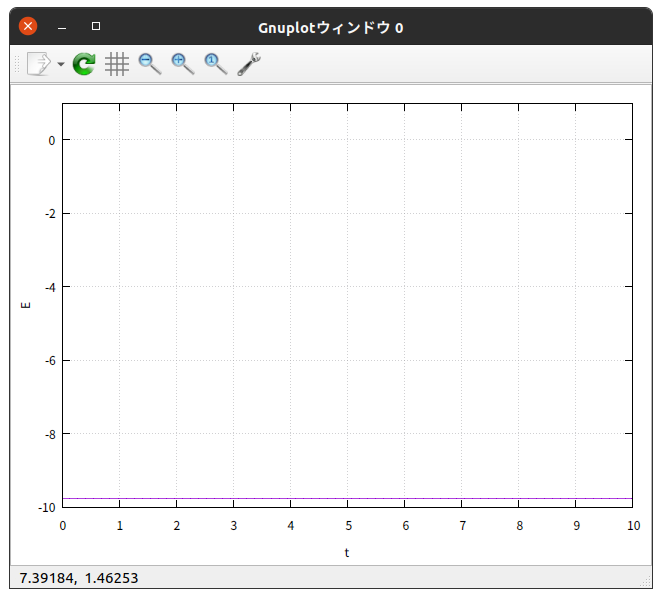
どれもちゃんと $E$ が保存している。
この計算結果は信用できる可能性が高くなった。
等時性の確認
上に示したグラフからもわかるが、はっきり比較するために上の4つの $x$-$t$グラフ を重ねてみると
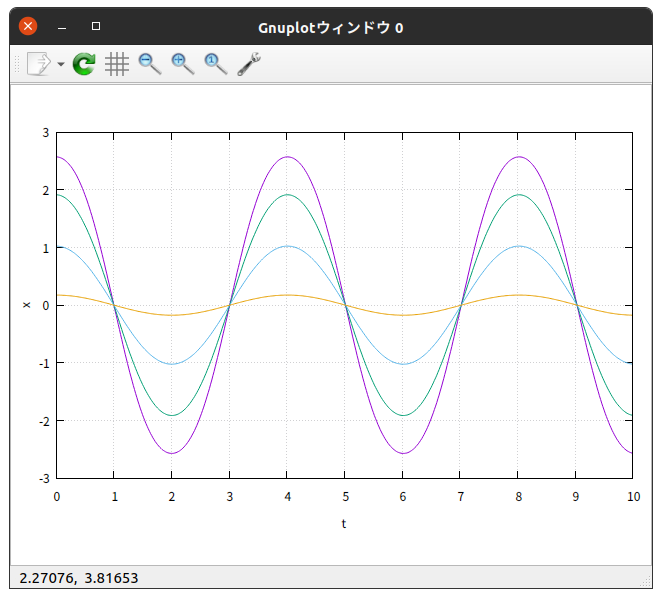
となる。
4つの場合の周期はぴったり一致している。
サイクロイド振り子において等時性が成り立つことが、見事に確かめられた!