この記事の前の話はこちら
この記事の続きはこちら
太陽系の惑星
Newtonの運動方程式が如何に凄いかを実感するには、やはり、実際の歴史と同じ、惑星の運動だろう。
ということで、まずは地球の運動、それからHalley彗星の運動をやってみた。
理屈
運動方程式
$x$-$y$平面 の原点に太陽があり、
1個の惑星が太陽からの万有引力を受けて $x$-$y$面 内で運動する。
太陽は動かないとする。
万有引力定数を $G$ 、
太陽の質量を $M$ 、
惑星の質量を $m$ 、
惑星の位置を ${\mathbf r}$ とすると、
太陽が惑星におよぼす 万有引力 ${\mathbf F}$ は
$$
{\mathbf F} = - G \hspace{0.1em} \frac{M \hspace{0.1em} m}{\left| {\mathbf r} \right|^{3}} \hspace{0.1em} {\mathbf r}
$$
である。
したがって、惑星の運動方程式は
$$
m \hspace{0.1em} \ddot{\mathbf r} = - G \hspace{0.1em} \frac{M \hspace{0.1em} m}{\left| {\mathbf r} \right|^{3}} \hspace{0.1em} {\mathbf r}
$$
である。
ある瞬間の惑星の 位置 と 速度 を初期条件として与え、この運動方程式を解けば、惑星の運動を知ることができる。
初期条件
今回は、惑星が近日点を通過する瞬間を初期状態(時刻 $t = 0$ )とする場合だけを扱う。
つまり、惑星の近日点の 位置 $\mathbf r_{0}$ と惑星が近日点を通過するときの 速度 $\mathbf v_{0}$ を初期条件として与えて、惑星の運動を調べようということである。
数値を与えるとき便利なように $\mathbf r_{0}$ と $\mathbf v_{0}$ を極座標で書く。
すなわち、 $\mathbf r_{0}$ をその 大きさ $r_{0}$ と 偏角 $\theta_{0}$ で、 $\mathbf v_{0}$ をその 大きさ $v_{0}$ と 偏角 $\phi_{0}$ で与える。
このとき、 $x$軸 を「遠日点と近日点を通る直線上に、近日点が正の側になるように」とれば、必然的に $\theta_{0} = 0$ となり、また $\mathbf v_{0}$ は $\mathbf r_{0}$ に直交するので $\phi_{0} = \frac{\pi}{2}$ とできる。
そして、 $r_{0}$ は(地球の場合もHalley彗星の場合も)文献から簡単に値を知ることができる。
問題は、 $v_{0}$ である。
これの値は、手近な文献には載っていない。
この値は得られるだろうか?
近日点での速度の大きさ
太陽から遠日点までの距離を $r_{1}$ とすると、
幾何学により楕円軌道の 半長軸 $a$ と 半短軸 $b$ が
$$
a = \frac{r_{0} + r_{1}}{2}
$$
$$
b = \sqrt{{r_{0}}^{2} - ( \hspace{0.1em} a - r_{0} \hspace{0.1em} )^{2}} = \sqrt{r_{0} \hspace{0.1em} r_{1}}
$$
であることが導かれる。
$a$ と $b$ が決まると楕円軌道の形は一意に定まるから、結局、 $r_{0}$ と $r_{1}$ が決まると軌道全体が定まると言える。
遠日点での惑星の速度の大きさを $v_{1}$ とすると、
力学的エネルギー保存則とケプラーの第2法則より
$$
\frac{1}{2} \hspace{0.1em} m \hspace{0.1em} {v_{0}}^{2} - \frac{G \hspace{0.1em} M \hspace{0.1em} m}{r_{0}} = \frac{1}{2} \hspace{0.1em} m \hspace{0.1em} {v_{1}}^{2} - \frac{G \hspace{0.1em} M \hspace{0.1em} m}{r_{1}}
$$
$$
\frac{1}{2} \hspace{0.1em} r_{0} \hspace{0.1em} v_{0} = \frac{1}{2} \hspace{0.1em} r_{1} \hspace{0.1em} v_{1}
$$
が成り立つ。
この2つの方程式より、初期条件( $r_{0} \hspace{0.1em} , \hspace{0.1em} v_{0}$ )が与えられれば $r_{1}$ と $v_{1}$ が定まる。
したがって、 $r_{0}$ と $v_{0}$ の2つから $r_{1} \hspace{0.1em} , \hspace{0.1em} v_{1}$ および楕円軌道全体が定まるのだと言える。
この因果関係により、 $r_{1}$ は $r_{0} \hspace{0.1em} , \hspace{0.1em} v_{0}$ の関数という形で表されるはずである。
ここで、手近な文献に、地球やHalley彗星の 近日点距離 ($r_{0}$)と 遠日点距離 ($r_{1}$)が記載されていることに留意しよう。
$r_{1}$ を $r_{0} \hspace{0.1em} , \hspace{0.1em} v_{0}$ の関数として表す式を $v_{0}$ について解けば、 $r_{0}$ と $r_{1}$ から $v_{0}$ を得る式になる。それを使えば文献の近日点距離と遠日点距離から $v_{0}$ を求められるのである。
実際の式は次のようになる。
力学的エネルギー保存則とケプラーの第2法則から $v_{1}$ を消去し $r_{1}$ について解くと
$$
r_{1} = r_{0} \hspace{1em} または \hspace{1em} r_{0} \cdot \frac{r_{0} \hspace{0.1em} {v_{0}}^{2}}{2 \hspace{0.1em} G \hspace{0.1em} M - r_{0} \hspace{0.1em} {v_{0}}^{2}}
$$
が導かれる。
$r_{1} = r_{0}$ はここで求める解ではないので、 $r_{1} = r_{0} \cdot \frac{r_{0} \hspace{0.1em} {v_{0}}^{2}}{2 \hspace{0.1em} G \hspace{0.1em} M - r_{0} \hspace{0.1em} {v_{0}}^{2}}$ を選ぶと
$$
r_{1} = \frac{r_{0}}{\frac{2 \hspace{0.1em} G \hspace{0.1em} M}{r_{0} \hspace{0.1em} {v_{0}}^{2}} - 1}
$$
が得られる。
これを $v_{0}$ について解くと
$$
v_{0} = \sqrt{\frac{2 \hspace{0.1em} G \hspace{0.1em} M \hspace{0.1em} r_{1}}{\left( \hspace{0.1em} r_{0} + r_{1} \hspace{0.1em} \right) \hspace{0.1em} r_{0}}}
$$
を得る。
この式を利用すれば、文献のデータから $v_{0}$ の値を知り、初期条件として与えることができる。
公転周期
ケプラーの第2法則より公転の面積速度が一定であるから、楕円軌道の面積を面積速度で割れば公転周期が求まる。
楕円の面積は $\pi \hspace{0.1em} a \hspace{0.1em} b$ であるから
$$
\pi \hspace{0.1em} a \hspace{0.1em} b = \pi \cdot \frac{r_{0} + r_{1}}{2} \cdot \sqrt{r_{0} \hspace{0.1em} r_{1}}
$$
が軌道の面積である。
面積速度は $\frac{1}{2} \hspace{0.1em} r_{0} \hspace{0.1em} v_{0}$ であるから
$$
\frac{1}{2} \hspace{0.1em} r_{0} \hspace{0.1em} v_{0} = \frac{1}{2} \cdot r_{0} \cdot \sqrt{\frac{2 \hspace{0.1em} G \hspace{0.1em} M \hspace{0.1em} r_{1}}{\left( \hspace{0.1em} r_{0} + r_{1} \hspace{0.1em} \right) \hspace{0.1em} r_{0}}}
$$
が公転の面積速度である。
よって、 公転周期 $T$ は
$$
T = \frac{\pi \cdot \frac{r_{0} + r_{1}}{2} \cdot \sqrt{r_{0} \hspace{0.1em} r_{1}}}{\frac{1}{2} \cdot r_{0} \cdot \sqrt{\frac{2 \hspace{0.1em} G \hspace{0.1em} M \hspace{0.1em} r_{1}}{\left( \hspace{0.1em} r_{0} + r_{1} \hspace{0.1em} \right) \hspace{0.1em} r_{0}}}
} = \pi \hspace{0.1em} \sqrt{\frac{\left( \hspace{0.1em} r_{0} + r_{1} \hspace{0.1em} \right)^{3}}{2 \hspace{0.1em} G \hspace{0.1em} M}}
$$
である。
$a$ を用いて表せば
$$
T = 2 \hspace{0.1em} \pi \hspace{0.1em} \sqrt{\frac{a^{3}}{G \hspace{0.1em} M}}
$$
である。
プログラム
運動方程式の関数 f
f <- function(f.t,f.rv) {
f.r <- sqrt( f.rv$x * f.rv$x + f.rv$y * f.rv$y + f.rv$z * f.rv$z )
f.F <- G * M * m / f.r / f.r
f.Fx <- - f.F / f.r * f.rv$x
f.Fy <- - f.F / f.r * f.rv$y
f.Fz <- - f.F / f.r * f.rv$z
f.ax <- f.Fx / m
f.ay <- f.Fy / m
f.az <- f.Fz / m
return( data.frame( x=f.rv$vx , y=f.rv$vy , z=f.rv$vz , vx=f.ax , vy=f.ay , vz=f.az ) )
}
G : 万有引力定数 $\hspace{0.5em} G$
M : 太陽の質量 $\hspace{0.5em} M$
m : 惑星の質量 $\hspace{0.5em} m$
f.t : 時刻 $\hspace{0.5em} t$
f.rv : 惑星の 位置 ${\mathbf r}$ と 速度 ${\mathbf v}$ を格納するデータフレーム
$\hspace{1em}$ 列 x y z : ${\mathbf r}$ の $x$成分 , $y$成分 , $z$成分
$\hspace{1em}$ 列 vx vy vz : ${\mathbf v}$ の $x$成分 , $y$成分 , $z$成分
f.r : ${\mathbf r}$ の大きさ $\hspace{0.5em} r$
f.F : 太陽と惑星がおよぼしあう 万有引力 ${\mathbf F}$ の大きさ $\hspace{0.5em} F$
f.Fx : ${\mathbf F}$ の $x$成分
f.Fy : ${\mathbf F}$ の $y$成分
f.Fz : ${\mathbf F}$ の $z$成分
f.ax : 惑星の 加速度 ${\mathbf a}$ の $x$成分
f.ay : ${\mathbf a}$ の $y$成分
f.az : ${\mathbf a}$ の $z$成分
境界条件の関数 boundary.condition
boundary.condition <- function(boundary.condition.t,boundary.condition.rv) {
return( boundary.condition.rv )
}
境界条件は、とくにない。
パラメータ
n <- 1
G <- 6.67430e-11
M <- 1.9884e30
m <- c( 5.9724e24 )
r0 <- 1.471e11
theta0.by.deg <- 0.0
theta0 <- theta0.by.deg / 180.0 * pi
v0 <- 30286.3692512291
phi0.by.deg <- 90.0
phi0 <- phi0.by.deg / 180.0 * pi
tunit <- 86400.0 * 50.0
t0 <- 0.0 * tunit
x0 <- r0 * cos(theta0)
y0 <- r0 * sin(theta0)
z0 <- 0.0
vx0 <- v0 * cos(phi0)
vy0 <- v0 * sin(phi0)
vz0 <- 0.0
tend <- 10.0 * tunit
Deltat <- 2.0e-4 * tunit
draw.step <- 100
xmin <- - 4.0 / 3.0 * r0
xmax <- 4.0 / 3.0 * r0
ymin <- - 4.0 / 3.0 * r0
ymax <- 4.0 / 3.0 * r0
n : 質点数 今回は 1
G : 万有引力定数 $\hspace{0.5em} G = 6.67430 \times 10^{-11} \hspace{0.2em} \textrm{m}^{3} \cdot \textrm{kg}^{-1} \cdot \textrm{s}^{-2}$
M : 太陽の質量 $\hspace{0.5em} M = 1.9884 \times 10^{30} \hspace{0.2em} \textrm{kg}$
m : 惑星の質量 $\hspace{0.5em} m$
r0 : 初期状態での 太陽-惑星 間の距離 $\hspace{0.5em} r_{0}$
theta0.by.deg : 初期状態での惑星の $x$-$y$平面 上の位置を極座標で表した場合の角度の値 $\hspace{0.5em} \theta_{0}$ (度)
theta0 : $\hspace{0.5em} \theta_{0}$ (rad)
v0 : 初期状態での惑星の速度の大きさ $\hspace{0.5em} v_{0}$
phi0.by.deg : 初期状態での惑星の $x$-$y$平面 内の速度を極座標で表した場合の角度の値 $\hspace{0.5em} \phi_{0}$ (度)
phi0 : $\hspace{0.5em} \phi_{0}$ (rad)
tunit : t0 , tend , Deltat を指定する際に単位として使う値
t0 : 初期状態の時刻
x0 y0 z0 : 初期状態での惑星の座標
vx0 vy0 vz0 : 初期状態での惑星の速度の各成分
tend : 終状態の時刻
Deltat : Runge-Kutta法の計算において1ステップで進める時間
draw.step : Runge-Kutta法で何ステップか計算するたびに画像を出力する、そのステップ数
時間に関するパラメータ t0 tend Deltat を指定するのに tunit という新たなパラメータをわざわざ用いたのは、単に数値を決めるときの便宜のためだ。 t0 から tend までの時間幅に対して Deltat をどれくらい細かくすれば十分な精度の計算結果が得られるのか、をよく考慮して適切な値に設定しなければならないのだが、前の「単振り子」のシミュレーションの経験から大体の目安が得られる( t0 $= 0 \hspace{0.2em} \mathrm{s}$ , tend $= 10 \hspace{0.2em}
\mathrm{s}$ に対して Deltat $= \frac{1}{5000} \hspace{0.2em} \mathrm{s}$ )ので、それらすべてに共通の tunit を掛けることで無難に今回の値を決めた、という経緯である。
結果を出力するコード
output <- function() {
plot(rv$x,rv$y,xlim=c(xmin,xmax),ylim=c(ymin,ymax),xlab="x",ylab="y",tcl=0.5,las=1,mgp=c(2.5,0.3,0),text(0.9*r0,1.2*r0,labels=paste("day ",as.character(round(t/86400,digits=3)))))
output.e <- m / 2.0 * ( rv$vx^2 + rv$vy^2 + rv$vz^2 ) - G * M * m / sqrt( rv$x * rv$x + rv$y * rv$y + rv$z * rv$z )
return( rbind( results , c( t/86400 , rv$x , rv$y , output.e ) ) )
}
単振り子やサイクロイド振り子のときと内容的には同じ。
数値データの $t$ (時刻)は「日」を単位として出力するようにしている。座標は $x$ と $y$ しか出力していない( $z$ を省略)。
力学的エネルギーは 運動エネルギー $\frac{1}{2} \hspace{0.1em} m \hspace{0.1em} v^{2}$ と ポテンシャルエネルギー $- \frac{G \hspace{0.1em} M \hspace{0.1em} m}{r}$ の和として計算している。
全リスト
################################################################
## parameters
## modify this section to change condition
################################################################
n <- 1
G <- 6.67430e-11
M <- 1.9884e30
m <- c( 5.9724e24 )
r0 <- 1.471e11
theta0.by.deg <- 0.0
theta0 <- theta0.by.deg / 180.0 * pi
v0 <- 30286.3692512291
phi0.by.deg <- 90.0
phi0 <- phi0.by.deg / 180.0 * pi
tunit <- 86400.0 * 50.0
t0 <- 0.0 * tunit
x0 <- r0 * cos(theta0)
y0 <- r0 * sin(theta0)
z0 <- 0.0
vx0 <- v0 * cos(phi0)
vy0 <- v0 * sin(phi0)
vz0 <- 0.0
tend <- 10.0 * tunit
Deltat <- 2.0e-4 * tunit
draw.step <- 100
xmin <- - 4.0 / 3.0 * r0
xmax <- 4.0 / 3.0 * r0
ymin <- - 4.0 / 3.0 * r0
ymax <- 4.0 / 3.0 * r0
################################################################
## output
## modify this section to change the method to output
################################################################
output <- function() {
plot(rv$x,rv$y,xlim=c(xmin,xmax),ylim=c(ymin,ymax),xlab="x",ylab="y",tcl=0.5,las=1,mgp=c(2.5,0.3,0),text(0.9*r0,1.2*r0,labels=paste("day ",as.character(round(t/86400,digits=3)))))
output.e <- m / 2.0 * ( rv$vx^2 + rv$vy^2 + rv$vz^2 ) - G * M * m / sqrt( rv$x * rv$x + rv$y * rv$y + rv$z * rv$z )
return( rbind( results , c( t/86400 , rv$x , rv$y , output.e ) ) )
}
################################################################
## models
## modify this section to change physical model
################################################################
f <- function(f.t,f.rv) {
f.r <- sqrt( f.rv$x * f.rv$x + f \hspace{0.2em} \mathrm{m}.rv$y * f.rv$y + f.rv$z * f.rv$z )
f.F <- G * M * m / f.r / f.r
f.Fx <- - f.F / f.r * f.rv$x
f.Fy <- - f.F / f.r * f.rv$y
f.Fz <- - f.F / f.r * f.rv$z
f.ax <- f.Fx / m
f.ay <- f.Fy / m
f.az <- f.Fz / m
return( data.frame( x=f.rv$vx , y=f.rv$vy , z=f.rv$vz , vx=f.ax , vy=f.ay , vz=f.az ) )
}
boundary.condition <- function(boundary.condition.t,boundary.condition.rv) {
return( boundary.condition.rv )
}
################################################################
## engines
## do not modify this section
################################################################
runge.kutta.4th <- function(runge.kutta.4th.t,runge.kutta.4th.rv) {
runge.kutta.4th.k0 <- f( runge.kutta.4th.t , runge.kutta.4th.rv ) * Deltat
runge.kutta.4th.k1 <- f( runge.kutta.4th.t + Deltat / 2.0 , runge.kutta.4th.rv + runge.kutta.4th.k0 / 2.0 ) * Deltat
runge.kutta.4th.k2 <- f( runge.kutta.4th.t + Deltat / 2.0 , runge.kutta.4th.rv + runge.kutta.4th.k1 / 2.0 ) * Deltat
runge.kutta.4th.k3 <- f( runge.kutta.4th.t + Deltat , runge.kutta.4th.rv + runge.kutta.4th.k2 ) * Deltat
runge.kutta.4th.Deltarv <- ( runge.kutta.4th.k0 + 2.0 * ( runge.kutta.4th.k1 + runge.kutta.4th.k2 ) + runge.kutta.4th.k3 ) / 6.0
return( runge.kutta.4th.rv + runge.kutta.4th.Deltarv )
}
### preparation to output
png(filename="%04d.png",width=960,height=960,units="px",res=192)
results <- matrix( c( 0 , 0 , 0 , 0 ) , nrow=1 , ncol=4 )
colnames(results) <- c( "t" , "x" , "y" , "E" )
###
t <- t0
rv <- data.frame( x=x0 , y=y0 , z=z0 , vx=vx0 , vy=vy0 , vz=vz0 )
while(t<=tend) {
results <- output()
for(i in 1:draw.step) {
rv <- runge.kutta.4th(t,rv)
rv <- boundary.condition(t,rv)
t <- t + Deltat
}
}
### post-processing to output
graphics.off()
write.table(as.data.frame(results[-1,]),file="results",sep=" ",row.names=FALSE,col.names=TRUE)
###
地球
質量
地球の質量は $\hspace{0.5em} m = 5.9724 \times 10^{24} \hspace{0.2em} \textrm{kg}$ である。
初期状態
地球が近日点にいる瞬間の時刻を $0 \hspace{0.2em} \mathrm{s}$ とした。
初期状態での位置
$r_{0}$ と $\theta_{0}$ を与えなければいけない。
座標軸を適切にとって、 $\theta_{0} = 0$ とした。
$r_{0}$ は、 wikipedia に記載の値を使って $1.471 \times 10^{11} \hspace{0.2em} \mathrm{m}$ とした。
初期状態での速度
$v_{0}$ と $\phi_{0}$ を与えなければいけない。
座標軸を適切にとって、 $\phi_{0} = \frac{\pi}{2}$ ( $90^{\circ}$ )とした。
$v_{0}$ は、『理屈』で説明した方法で決めた。
wikipedia に記載の 値 $r_{0} = 1.471 \times 10^{11} \hspace{0.2em} \mathrm{m}$ 、 $r_{1} = 1.521 \times 10^{11} \hspace{0.2em} \mathrm{m}$ を使って
$$
v_{0} = \sqrt{\frac{2 \hspace{0.1em} G \hspace{0.1em} M \hspace{0.1em} r_{1}}{\left( \hspace{0.1em} r_{0} + r_{1} \hspace{0.1em} \right) \hspace{0.1em} r_{0}}}
$$
を計算すると、 $v_{0} = 30286.3692512291 \hspace{0.2em} \mathrm{m}/\mathrm{s}$ となる。
この値を $v_{0}$ に設定した。
計算開始と終了の時刻、ステップの時間刻み幅、画像出力の頻度
t0 は 0、 tunit は $50 \hspace{0.2em} 日$ 、 tend はその $10 \hspace{0.2em} 倍$ の $500 \hspace{0.2em} 日$ 、 Deltat は tunit の $\frac{1}{5000}$ すなわち $\frac{1}{100}$日 とした。そして、 draw.step を 100 としたから画像の出力は $1 \hspace{0.2em} 日$ ごとである。
実行結果
計算にかかった時間は 4分56秒 。
結果は次のようになった。
ほぼ円に近い軌道で、周期 $365 \hspace{0.2em} 日$ で公転しているように見える。
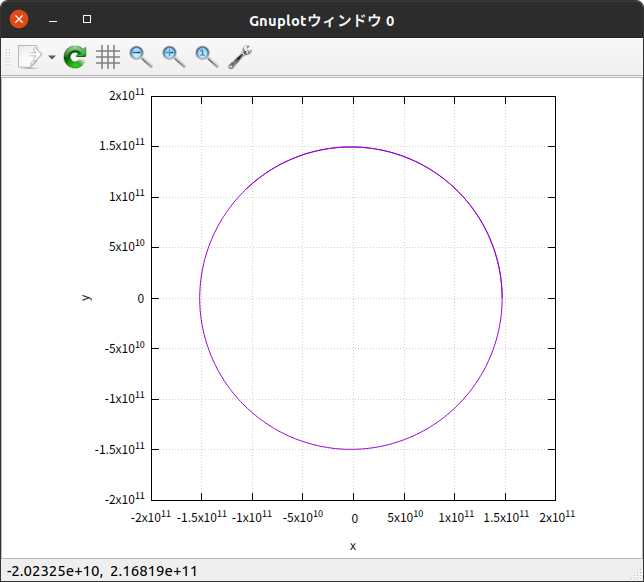
出力した数値データを使って $x$-$y$平面 上に軌道をプロットしてみると
かなり円に近いが、完全な円ではない。
右端の $y = 0$ になる点での 太陽-地球 間の距離が $1.5 \times 10^{11} \hspace{0.2em} \mathrm{m}$ よりも小さく(初期値で設定した $r_{0}$ であるはず)、左端の $y = 0$ になる点での 太陽-地球 間の距離が $1.5 \times 10^{11} \hspace{0.2em} \mathrm{m}$ よりも大きくなっており、右端が近日点、左端が遠日点になっている。
つまり、この軌道は円ではなく楕円と考えられる。
公転周期
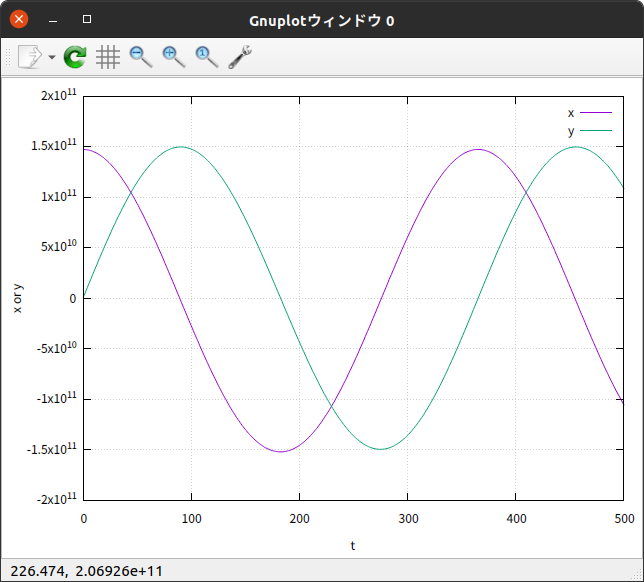
横軸に $t$ 、縦軸に $x$ および $y$ をプロットしたグラフを描いてみた。
周期はほぼ $365 \hspace{0.2em} 日$ くらいに見えるが…。
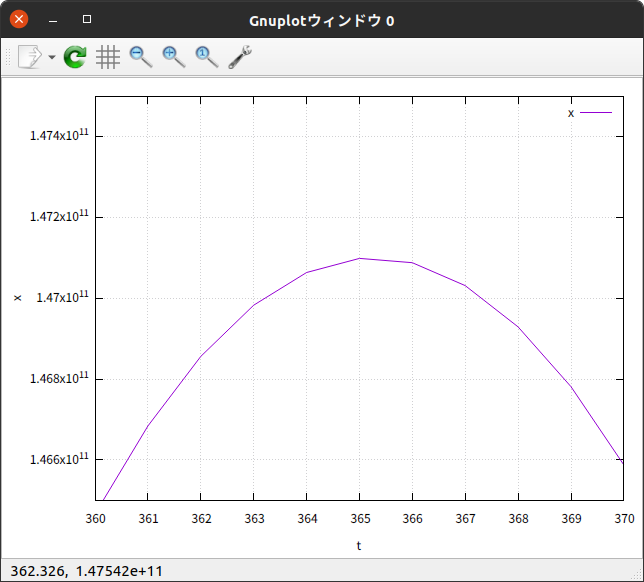
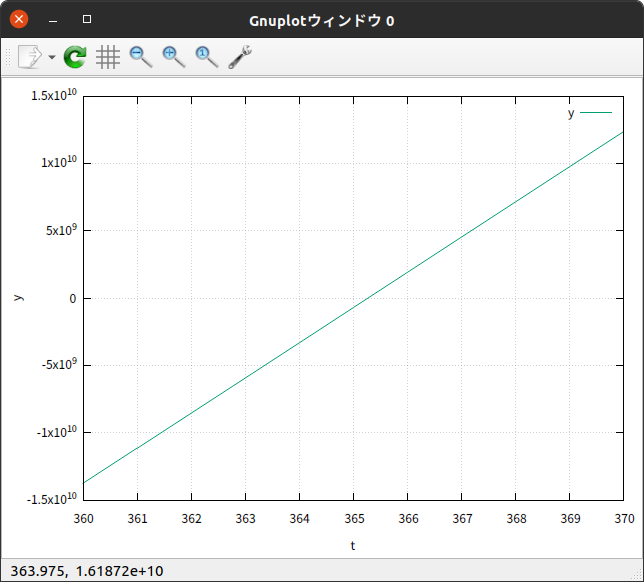
気になる部分を拡大して見ると
$x$-$t$グラフ を見ると、きっちり $365 \hspace{0.2em} 日$ になっている。
さらに、 $y$-$t$グラフ からは、もっと細かく読み取ることができて、だいたい $365.25 \hspace{0.2em} 日$ くらいである。
現実の地球の公転周期に、ものすごく近い。
遠日点の距離
出力した数値データを確認すると
"t" "x" "y" "E"
181 -152042919258.211 4131649936.23367 -2.64909038114596e+33
182 -152091426070.661 1601414925.19038 -2.64909038114596e+33
183 -152097112987.773 -929270950.063884 -2.64909038114595e+33
184 -152059978488.708 -3459695197.79002 -2.64909038114595e+33
185 -151980032504.376 -5989145388.83149 -2.64909038114595e+33
$t = 183 \hspace{0.2em} 日$ の $x = -152097112987.773 \hspace{0.2em} \mathrm{m}$ が最も遠日点に近い値だと考えられる。
つまり、「シミュレーションの結果、遠日点の太陽からの距離が $1.521 \times 10^{11} \hspace{0.2em} \mathrm{m}$ であった」と言える。
wikipedia に記載されている遠日点距離は $1.521 \times 10^{11} \hspace{0.2em} \mathrm{m}$ である。見事に一致している。
力学的エネルギーの保存
縦軸に地球の力学的エネルギー $E$ 、横軸に時刻 $t$ をとったグラフは
となった。
$E$ はちゃんと保存している。
離心率
シミュレーションの結果として得られた楕円軌道の離心率を測ってみる。
楕円の離心率 $e$ は
$$
e = \sqrt{1 - \frac{b^{2}}{a^{2}}}
$$
で与えられる。
$a$ は太陽から近日点までの距離と太陽から遠日点までの距離の和の $\frac{1}{2}$ 倍 に等しく、 $b$ は軌道上で最大の $y$ の絶対値に等しい。
出力した数値データから、これらの値を読み取る。
太陽から近日点までの距離は $1.471 \times 10^{11} \hspace{0.2em} \mathrm{m}$ 、太陽から遠日点までの距離は $1.52097112987773 \times 10^{11} \hspace{0.2em} \mathrm{m}$ である。
よって、 $a = 1.4959855649 \times 10^{11} \hspace{0.2em} \mathrm{m}$ である。
軌道上で最大の $y$ の絶対値は
"t" "x" "y" "E"
88 3534732303.84971 149457359057.022 -2.64909038114596e+33
89 961322963.283309 149539067100.047 -2.64909038114596e+33
90 -1612371263.75905 149576476543.792 -2.64909038114596e+33
91 -4185588372.48145 149569614512.07 -2.64909038114596e+33
92 -6757567812.53559 149518521188.947 -2.64909038114597e+33
273 -7440389768.01516 -149497522939.654 -2.64909038114597e+33
274 -4868866678.25398 -149560355835.917 -2.64909038114598e+33
275 -2295904187.6895 -149578970301.753 -2.64909038114598e+33
276 277737576.89991 -149553322693.667 -2.64909038114597e+33
277 2851296975.33677 -149483382413.654 -2.64909038114597e+33
より、
$t = 90 \hspace{0.2em} 日$ における $149576476543.792 \hspace{0.2em} \mathrm{m}$
あるいは
$t = 275 \hspace{0.2em} 日$ における $149578970301.753 \hspace{0.2em} \mathrm{m}$
である。
ここでは、両者の平均をとって $b = 1.4957772342 \times 10^{11} \hspace{0.2em} \mathrm{m}$ としてみよう。
この $a$ と $b$ の値より、 $e = 0.0166883274$ が得られる。
wikipedia に記載されている地球の軌道の離心率は $0.01671022$ である。 0.2 % 以下の精度で一致している。
Halley彗星
質量
Halley彗星の質量は $\hspace{0.5em} m = 2.2 \times 10^{14} \hspace{0.2em} \textrm{kg}$ である(wikipedia に記載されている値)。
初期状態
Halley彗星が近日点にいる瞬間の時刻を $0 \hspace{0.2em} \mathrm{s}$ とした。
初期状態での位置
$\theta_{0} = 0$ とした。
$r_{0}$ は、 wikipedia に記載されている値が $0.58597811 \hspace{0.2em} \mathrm{au}$ で $1 \hspace{0.2em} \mathrm{au} = 1.49597870700 \times 10^{11} \hspace{0.2em} \mathrm{m}$ であるから、 $8.76610775328 \times 10^{10} \hspace{0.2em} \mathrm{m}$ とした。
初期状態での速度
$\phi_{0} = \frac{\pi}{2}$ とした。
$v_{0}$ は次のとおり。
wikipedia に記載の値より得られる $r_{0} = 8.76610775328 \times 10^{10} \hspace{0.2em} \mathrm{m}$ 、 $r_{1} = 5.2482389455 \times 10^{12} \hspace{0.2em} \mathrm{m}$ を使って
$$
v_{0} = \sqrt{\frac{2 \hspace{0.1em} G \hspace{0.1em} M \hspace{0.1em} r_{1}}{\left( \hspace{0.1em} r_{0} + r_{1} \hspace{0.1em} \right) \hspace{0.1em} r_{0}}}
$$
を計算すると、 $v_{0} = 54571.9273756948 \hspace{0.2em} \mathrm{m}/\mathrm{s}$ となる。
この値を $v_{0}$ に設定した。
計算開始と終了の時刻、ステップの時間刻み幅、画像出力の頻度
t0 は 0、 tunit は $50 \hspace{0.2em} 日$ 、 tend はその $600 \hspace{0.2em} 倍$ の $30000 \hspace{0.2em} 日$ 、 Deltat は tunit の $\frac{1}{5000}$ すなわち $\frac{1}{100} \hspace{0.2em} 日$ とした。そして、 draw.step を 3000 としたから画像の出力は $30 \hspace{0.2em} 日$ ごとである。
画像の出力
細かい点だが、画像を出力するコードを次のように修正(日数を表示する位置の修正)。
plot(rv$x,rv$y,xlim=c(xmin,xmax),ylim=c(ymin,ymax),xlab="x",ylab="y",tcl=0.5,las
=1,mgp=c(2.5,0.3,0),text(35.0*r0,55.0*r0,labels=paste("day ",as.character(round(
t/86400,digits=1)))))
実行結果
計算にかかった時間は 4時間52分8秒 。
結果は次のようになった(アニメーションは30日1コマでなく60日1コマに間引きしてある)。
周期 およそ $27500 \hspace{0.2em} 日$ で公転しているように見える。
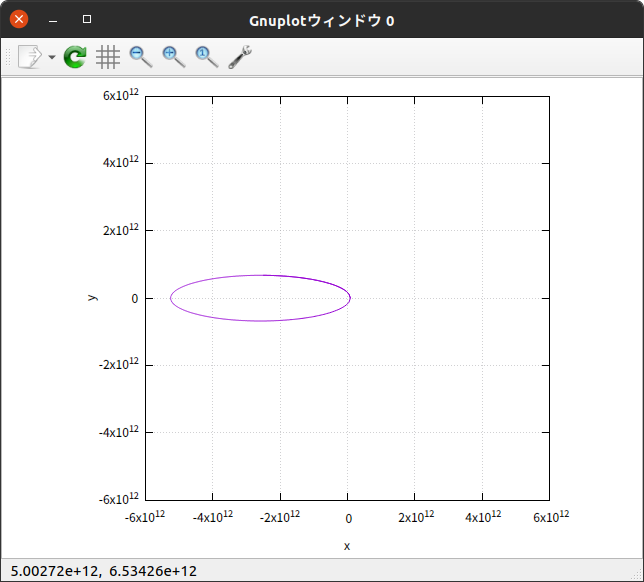
出力した数値データを使って $x$-$y$平面 上に軌道をプロットしてみると
かなり離心率の大きい楕円軌道である。
公転周期
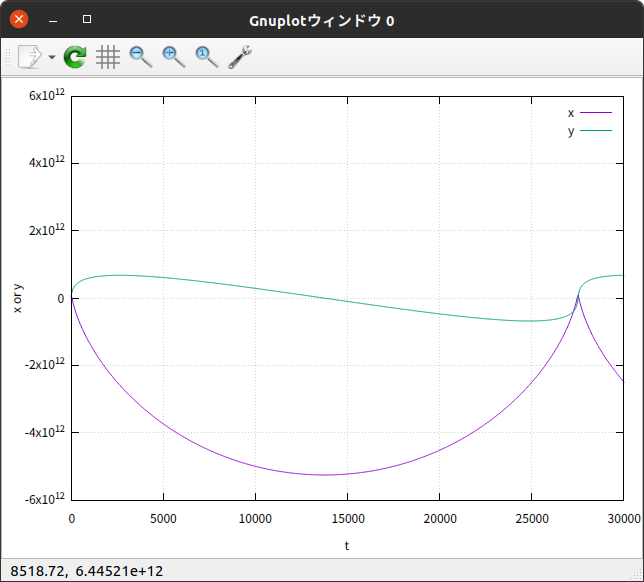
横軸に $t$ 、縦軸に $x$ および $y$ をプロットしたグラフを描いてみた。
周期はやはりほぼ $27500 \hspace{0.2em} 日$ くらいに見える。
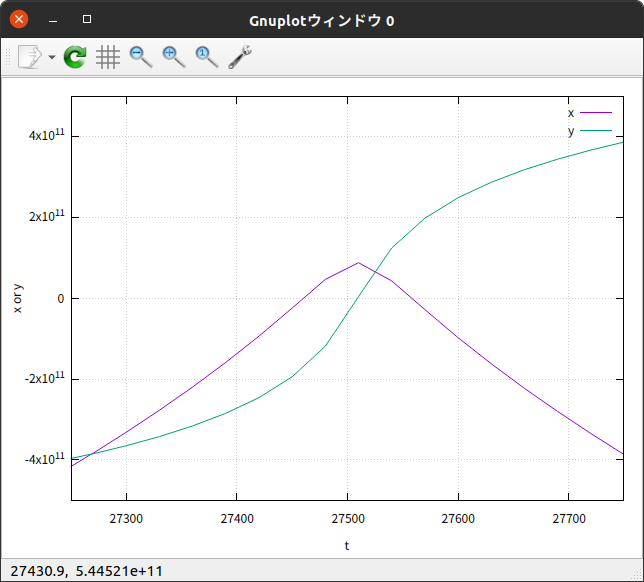
気になる部分を拡大して見ると
データの出力が $30 \hspace{0.2em} 日$ ごとであることに留意すると、公転周期が $27510 \hspace{0.2em} 日$ になっていることがわかる。
年に直すと $75.3169630605 \hspace{0.2em} 年$ であり、よく知られているHalley彗星の公転周期( wikipedia には箇所によって $75.3 \hspace{0.2em} 年$ あるいは $75.32 \hspace{0.2em} 年$ と記載されている)とほぼ一致している。
遠日点の距離
出力した数値データを確認すると
"t" "x" "y" "E"
13680 -5248138866114.95 5874955689.22595 -5.47172768192346e+21
13710 -5248203175030.85 3512345367.14299 -5.47172768192345e+21
13740 -5248235112781.99 1149713380.6835 -5.47172768192346e+21
13770 -5248234679742.96 -1212925697.15829 -5.47172768192346e+21
13800 -5248201875908.69 -3575557293.72515 -5.47172768192346e+21
$t = 13740 \hspace{0.2em} 日$ の $x = -5248235112781.99 \hspace{0.2em} \mathrm{m}$ が最も遠日点に近い値だと考えられる。
つまり、「シミュレーションの結果、遠日点の太陽からの距離が $5.24823511278199 \times 10^{12} \hspace{0.2em} \mathrm{m}$ であった」と言える。
wikipedia に記載されている値によると遠日点距離は $r_{1} = 5.2482389455 \times 10^{12} \hspace{0.2em} \mathrm{m}$ である。
$6 \hspace{0.2em} 桁$ 目まで一致している。
力学的エネルギーの保存
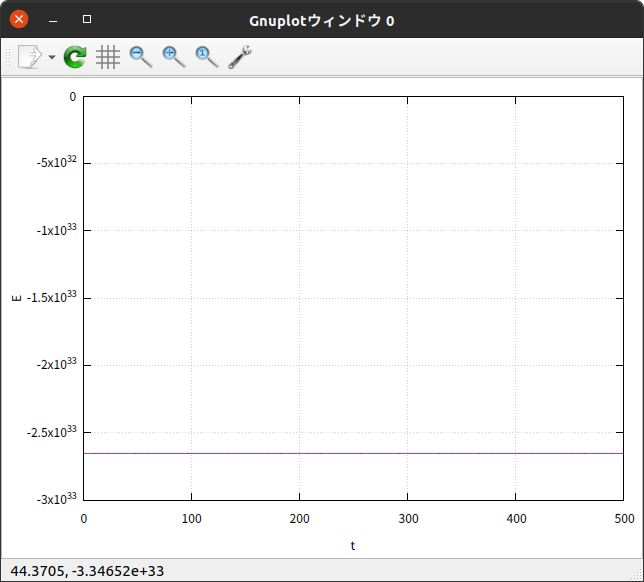
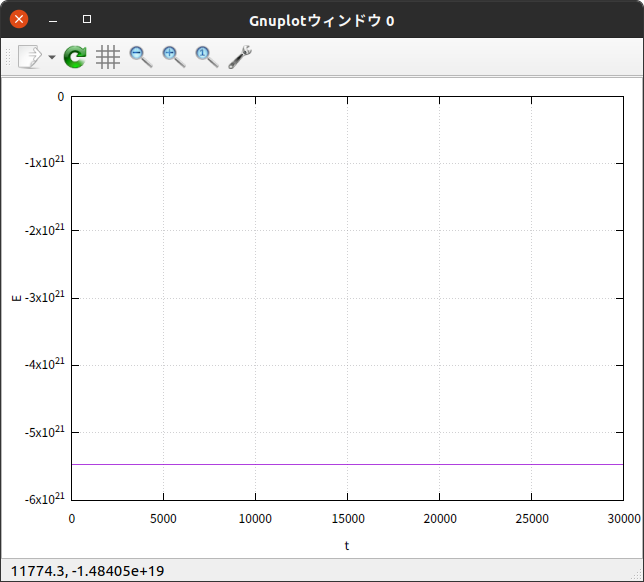
縦軸にHalley彗星の力学的エネルギー $E$ 、横軸に時刻 $t$ をとったグラフは
となった。
$E$ はちゃんと保存している。
離心率
シミュレーションの結果として得られた楕円軌道の離心率を測ってみる。
楕円の離心率 $e$ は
$$
e = \sqrt{1 - \frac{b^{2}}{a^{2}}}
$$
で与えられ、 $a$ は太陽から近日点までの距離と太陽から遠日点までの距離の和の $\frac{1}{2}$ 倍 に等しく、 $b$ は軌道上で最大の $y$ の絶対値に等しい。
出力した数値データから、これらの値を読み取る。
太陽から近日点までの距離は $8.76610775328 \times 10^{10} \hspace{0.2em} \mathrm{m}$ 、太陽から遠日点までの距離は $5.24823511278199 \times 10^{12} \hspace{0.2em} \mathrm{m}$ である。
よって、 $a = 2.6679480952 \times 10^{12} \hspace{0.2em} \mathrm{m}$ である。
軌道上で最大の $y$ の絶対値は
"t" "x" "y" "E"
2580 -2541672248059.29 678210804156.36 -5.47172768192358e+21
2610 -2560148915987.01 678262533247.143 -5.47172768192358e+21
2640 -2578502706817.51 678281707617.426 -5.47172768192362e+21
2670 -2596735195110.89 678268972295.589 -5.47172768192353e+21
2700 -2614847915280.66 678224952738.478 -5.47172768192359e+21
24810 -2614364856347.68 -678226532552.352 -5.47172768192393e+21
24840 -2596248951427.73 -678269723081.317 -5.47172768192391e+21
24870 -2578013237841.09 -678281612888.727 -5.47172768192386e+21
24900 -2559656180119.34 -678261576004.806 -5.47172768192379e+21
24930 -2541176202607.63 -678208966866.042 -5.47172768192378e+21
より、
$t = 2640 \hspace{0.2em} 日$ における $678281707617.426 \hspace{0.2em} \mathrm{m}$
あるいは
$t = 24870 \hspace{0.2em} 日$ における $678281612888.727 \hspace{0.2em} \mathrm{m}$
である。
ここでは、両者の平均をとって $b = 6.782816602531 \times 10^{11} \hspace{0.2em} \mathrm{m}$ としてみよう。
この $a$ と $b$ の値より、 $e = 0.9671428802$ が得られる。
wikipedia に記載されているHalley彗星の軌道の離心率は $0.96714291$ である。 $3 \times 10^{-8}$ 程度の精度で一致している。
Deltat への計算結果の依存性
地球についてもHalley彗星についても、かなりの精度で文献値を再現する結果となった。
このプログラムが運動方程式を数値的に解くツールとして有効だということで喜ばしい。
当然このことは Deltat をどれくらいの大きさにとるか、に依存するはずである。
Deltat をいくらにすると結果の精度がどれくらいになるのか、今後のために、調べてみた。
上のHalley彗星のシミュレーションでは、 Deltat を tunit の $\frac{1}{5000}$ にした。
そこで、 Deltat を tunit の $\frac{1}{2000} \hspace{0.1em} , \hspace{0.1em} \frac{1}{1000} \hspace{0.1em} , \hspace{0.1em} \frac{1}{500} \hspace{0.1em} , \hspace{0.1em} \frac{1}{200} \hspace{0.1em} , \hspace{0.1em} \frac{1}{100} \hspace{0.1em} , \hspace{0.1em} \frac{1}{50} \hspace{0.1em} , \hspace{0.1em} \frac{1}{20} \hspace{0.1em} , \hspace{0.1em} \frac{1}{10} \hspace{0.1em} , \hspace{0.1em} \frac{1}{5} \hspace{0.1em} , \hspace{0.1em} \frac{1}{2} \hspace{0.1em} , \hspace{0.1em} 1 \hspace{0.2em} 倍$ にして計算し、結果を比較してみた。
次のようになった。
Deltat / tunit
|
$計算時間$ / $分$ | $T$ / $日$ | $r_{0}$ / $\mathrm{m}$ | $r_{1}$ / $\mathrm{m}$ | $a$ / $\mathrm{m}$ | $b$ / $\mathrm{m}$ | $e$ |
|---|---|---|---|---|---|---|---|
| $\frac{1}{5000}$ | 292.1375 | 27510 | 8.76610775328e10 | 5248235112781.99 | 2667948095157.4 | 678281611966.553 | 0.96714288494146 |
| $\frac{1}{2000}$ | 117.0565 | 27510 | 8.76610775328e10 | 5248235112780.21 | 2667948095156.5 | 678281611966.438 | 0.967142884941449 |
| $\frac{1}{1000}$ | 59.04795 | 27510 | 8.76610775328e10 | 5248235112745.39 | 2667948095139.09 | 678281611964.188 | 0.967142884941234 |
| $\frac{1}{500}$ | 29.56077 | 27510 | 8.76610775328e10 | 5248235112172.63 | 2667948094852.71 | 678281611927.176 | 0.967142884937707 |
| $\frac{1}{200}$ | 12.09343 | 27510 | 8.76610775328e10 | 5248235088456.18 | 2667948082994.49 | 678281610394.62 | 0.967142884791667 |
| $\frac{1}{100}$ | 6.236133 | 27510 | 8.76610775328e10 | 5248234710742.79 | 2667947894137.79 | 678281585986.791 | 0.967142882465803 |
| $\frac{1}{50}$ | 3.210033 | 27510 | 8.76610775328e10 | 5248228266977.65 | 2667944672255.23 | 678281169590.724 | 0.967142842786654 |
| $\frac{1}{20}$ | 1.499567 | 27510 | 8.76610775328e10 | 5247918535412.44 | 2667789806472.62 | 678261154437.292 | 0.96714093542148 |
| $\frac{1}{10}$ | 0.925967 | 27450 | 8.76610775328e10 | 5241837031393.42 | 2664749054463.11 | 677868042043.052 | 0.967103439858256 |
| $\frac{1}{5}$ | 0.643283 | 26430 | 8.76610775328e10 | 5107619735250.75 | 2597640406391.77 | 669133357126.87 | 0.966253574853124 |
| $\frac{1}{2}$ | 0.540167 | 7125 | 8.76610775328e10 | 2079165806284.22 | 1083413441908.51 | 426921438848.212 | 0.919088065421841 |
| $1$ | 0.275533 | 測定不能 | 8.76610775328e10 | 測定不能 | 測定不能 | 測定不能 | 測定不能 |
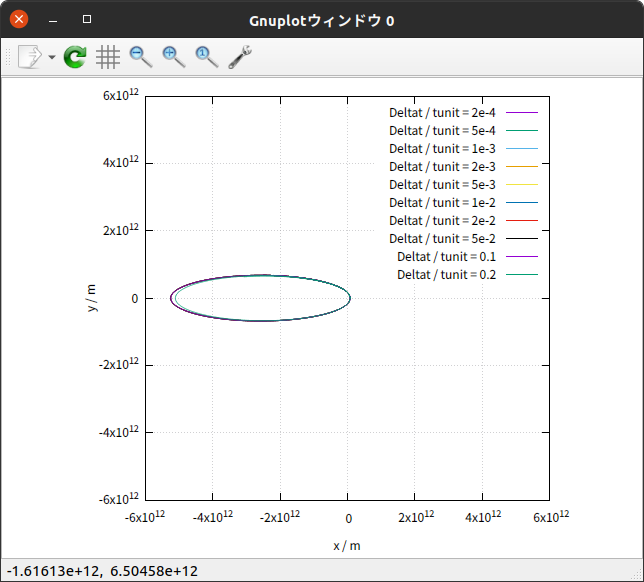
軌道については、 Deltat が tunit の $\frac{1}{10} \hspace{0.2em} 倍$ 以下の場合は、グラフソフトで描くと区別できないくらいの、どれもほぼ同じ楕円という結果であった。
Deltat が tunit の $\frac{1}{5} \hspace{0.2em} 倍$ の場合は、 $\frac{1}{10} \hspace{0.1em} 倍$ 以下の場合と似た楕円であるものの半長軸が少し小さいという結果であった。
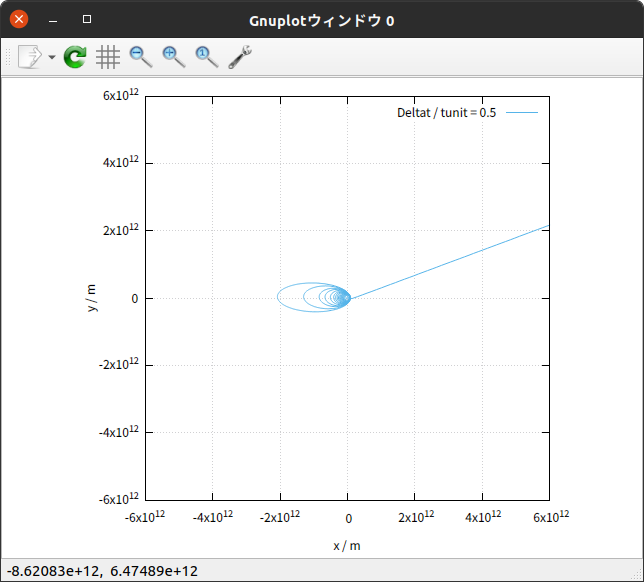
Deltat が tunit の $\frac{1}{2} \hspace{0.2em} 倍$ の場合は、一定の軌道を周期的に回る結果にならず、螺線(渦巻)を描いて太陽へ落下していくような結果となった。
上の表では、これについて、太陽の周りを1回りして最初に $x$ が極大となる(このとき同時に $\theta$ が最も $0$ に近い値となった)までの時間を $T$ とした。また、 $r_{0}$ は初期状態での $x$ の値、 $r_{1}$ は $x$ が最初に極小(負で絶対値が極大)となるときの $x$ の絶対値とした。
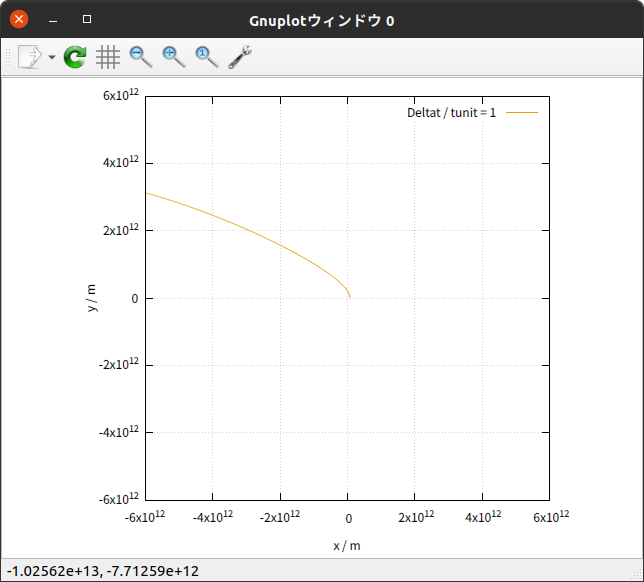
Deltat が tunit の $1 \hspace{0.2em} 倍$ の場合は、太陽の周りを回りすらせず、楕円でも何でもない軌道を描く結果となった。
上の表では、これについて、 $T \hspace{0.1em} , \hspace{0.1em} r_{1} \hspace{0.1em} , \hspace{0.1em} a \hspace{0.1em} , \hspace{0.1em} b \hspace{0.1em} , \hspace{0.1em} e$ は定義できないため「測定不能」とした。 $r_{0}$ は初期状態での $x$ の値とした。
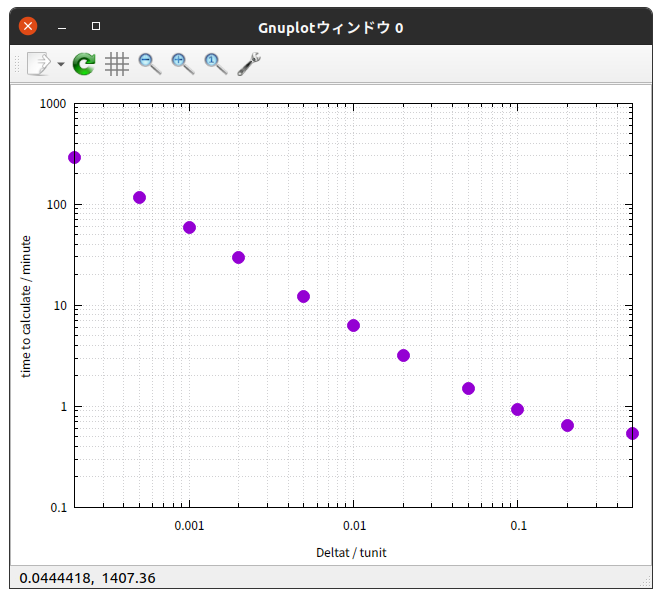
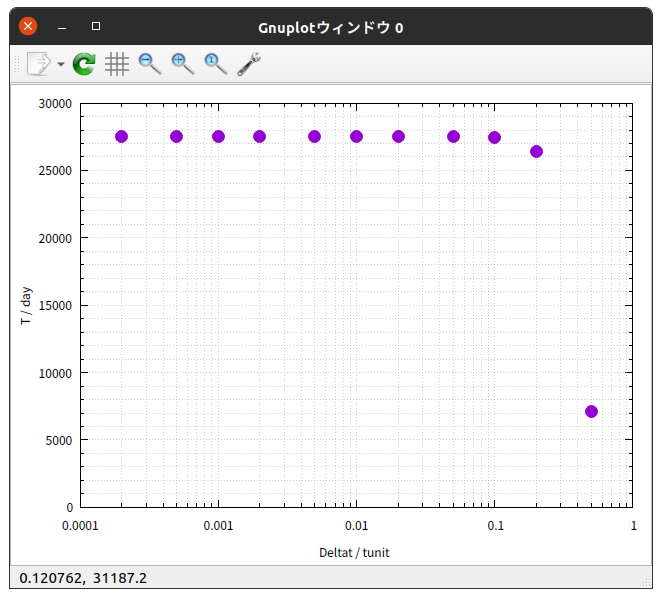
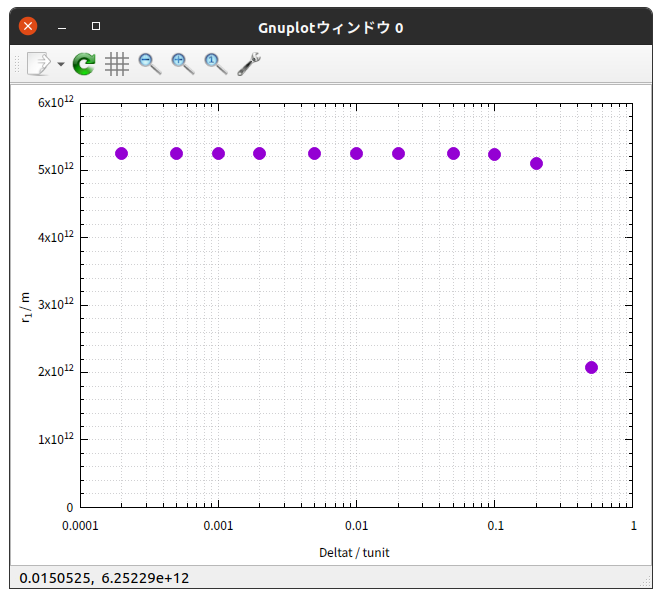
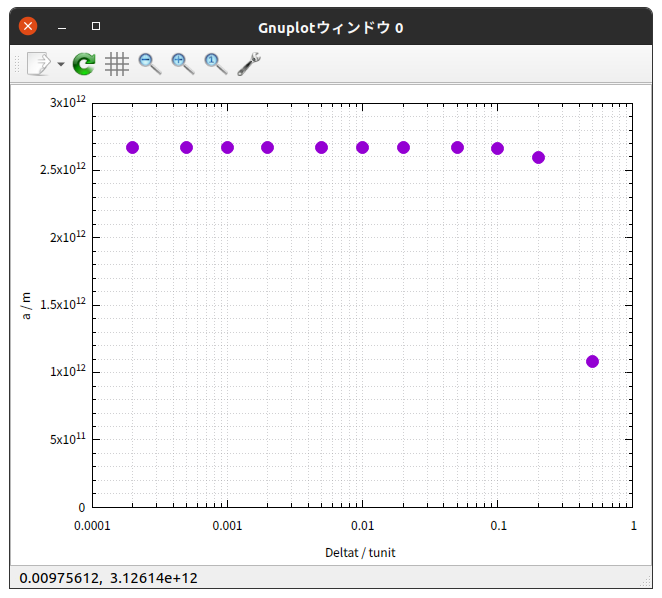
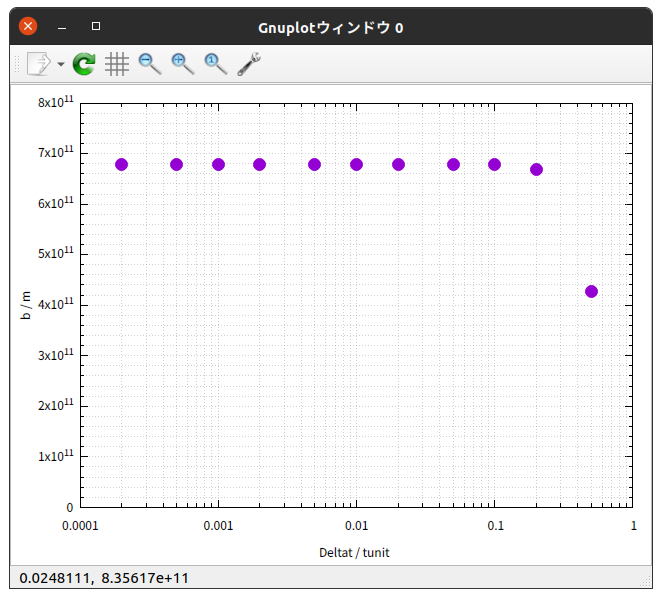
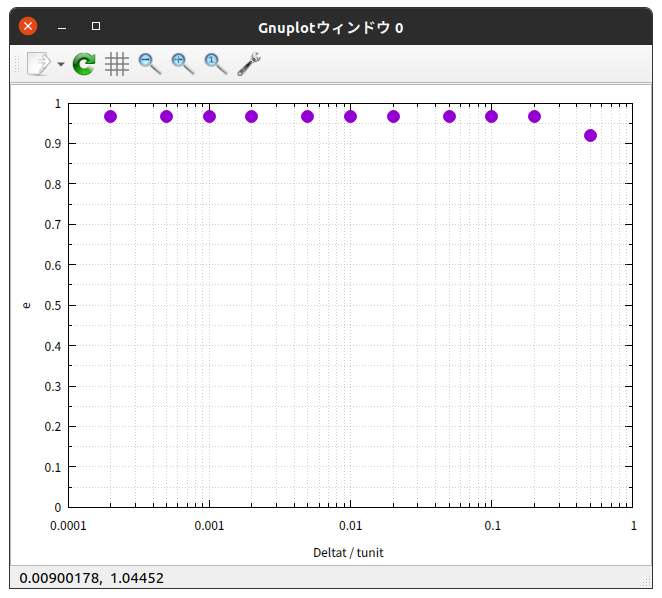
上の表の内容をグラフで表すと次のようになる。
これらのグラフから、次のように言えそうだ。
まず、 Deltat / tunit が 1 の場合では、軌道らしきものすら描けないほど、まったく計算できていない。
Deltat / tunit が $\frac{1}{2}$ の場合では、「軌道らしきもの」は描かれるものの、現実とはかけ離れた意味のないものであり、やはりまったく計算できていないと言える。
Deltat / tunit が $\frac{1}{5}$ の場合では、正しい値( Deltat / tunit $= \frac{1}{5000}$ の場合の値)から、 $T$ と $r_{1}$ ははっきりずれており、 $a$ と $b$ は少しずれている。
Deltat / tunit が $\frac{1}{10}$ の場合では、 $T \hspace{0.1em} , \hspace{0.1em} r_{1} \hspace{0.1em} , \hspace{0.1em} a \hspace{0.1em} , \hspace{0.1em} b$ が、正しい値からほんの僅かにずれている。
Deltat / tunit が $\frac{1}{20}$ 以下の場合では、 $T \hspace{0.1em} , \hspace{0.1em} r_{1} \hspace{0.1em} , \hspace{0.1em} a \hspace{0.1em} , \hspace{0.1em} b \hspace{0.1em} , \hspace{0.1em} e$ のいずれも、正しい値からのずれはほとんど無い。
総合すると、 Deltat / tunit が $\frac{1}{20}$ 以下であれば、今回のRunge-Kutta法によるシミュレーションは正確と考えていいと判断できそうである。
数値の表を見ると、 $r_{1} \hspace{0.1em} , \hspace{0.1em} a \hspace{0.1em} , \hspace{0.1em} b$ が、 Deltat / tunit $= \frac{1}{20}$ だと $4 \hspace{0.2em} 桁$ 、 Deltat / tunit $= \frac{1}{10}$ だと $3 \hspace{0.2em} 桁$ の精度で正確に計算されていることがわかる。 $e$ はそれぞれ $5 \hspace{0.2em} 桁$ と $4 \hspace{0.2em} 桁$ 。
なんとなく興味本位で計算してみるくらいなら $4 \hspace{0.2em} 桁$ の精度で満足できるので、やはり Deltat / tunit $= \frac{1}{20}$ 以下でよい。
Deltat / tunit $= \frac{1}{20}$ なら、わずか $1.5 \hspace{0.1em} 分$ 程度で計算が終わる。
最初の計算では $5 \hspace{0.1em} 時間$ もの時間をかけて計算したわけだが、どうやら無駄だったと言える。トホホだ。