はじめに
非エンジニアの界隈も含めて世間一般で、「ディープラーニングって、すっごーい」、と言われるようになって2年ほどが経過しました。あえて、「ニューラルネット」「ディープラーニング」に冷水を浴びせてみようということで、NIPS 2017の論文 On the Complexity of Learning Neural Networksについて、触れてみます。「だって、ニューラルネットなんだから、なんだって、できるでしょ」と、無茶振りをしてくる近所のおじさん&おばさん、に出会った時に撃退する話のネタになります。(冗談です。)
結論は何?
結論:SGDのような局所的な情報を「問い合わせる」手法では、ユニット数が入力次元のルートぐらいのNNを学習するための問い合わせの回数が膨大になってしまう。
実際には、ユニット数が入力次元のルートぐらいの単層のNNで生成されるデータ構造は複雑すぎて、局所的な情報を少ない回数問い合わせただけでは、fittingに必要な情報が取得できないということを述べています。
より形式的な記述
Statistical Query Algorithm a.k.a SQ Algorithmは、ある固定された確率分布上での計算問題です。
損失関数が少なくなる方向へ向かって、勾配を求めてパラメータに足しこむプロセスを抽象的に表現しています。
任意の整数 $t>0$と$X$上の分布$D$に対して、VSTAT(t)というオラクル(クエリに対して、答えを返すデータベースのようなもの)は、期待値$p=E_{D}[ f(X)]$を満たすクエリ関数 $f: X \rightarrow [0,1]$を入力として受け取ります。返答として、以下の(1)を満たすような実数$v$を返します。$| v - p| \leq \max ${$ \frac{1}{t} , \sqrt{ \frac{p(1-p)}{t} } $} (1)
ある$\gamma > 0, m : (\delta, \gamma) \rightarrow \mathbb{N}$と、アルゴリズムが存在して、 すべての$\delta \in (0, 1]$に対してそのアルゴリズムが$m(\delta, \gamma)$個のサンプルを$X \times Y$上の分布$D$から見た後に,$h \in H$を計算できて、条件$ error(h) \leq 0.5 -\gamma $を確率$1 - \delta$で満たすような学習問題を、弱学習が可能な問題であると定義します。
以下の数学定理で表現されます。
任意に$n \in \mathbb{N}, \lambda, s \geq 1$をとる。
このときある関数族 $\mathcal{C} \in { f : f:\mathbb{R} \rightarrow [-1,1] }$が存在して、この関数は中間層が$O(s\sqrt{n} \log (\lambda sn))$個数のsigmoidで、 sharpnessがsで、出力次元が1であり、重み行列の特異値の最小値と最大値の比が$(n, s, \lambda)$のたかだか多項式オーダーであり、 整数$t = \Omega (s^2 n)$
どんな (randomized) SQ アルゴリズム Aで、
$\lambda $-Lipschitz クエリをVSTAT(t)へ入力して、 $\mathcal{C}$を少なくとも確率$1/2$で弱学習し、回帰の誤差$1/\sqrt{t}$以下であり、入力が分散1の$\mathbb{R}$上のlog-concaveな分布からi.i.dでサンプルされるとき、問い合わせ回数として、$2^{\Omega (n)}/\lambda s^2 $個が必要.
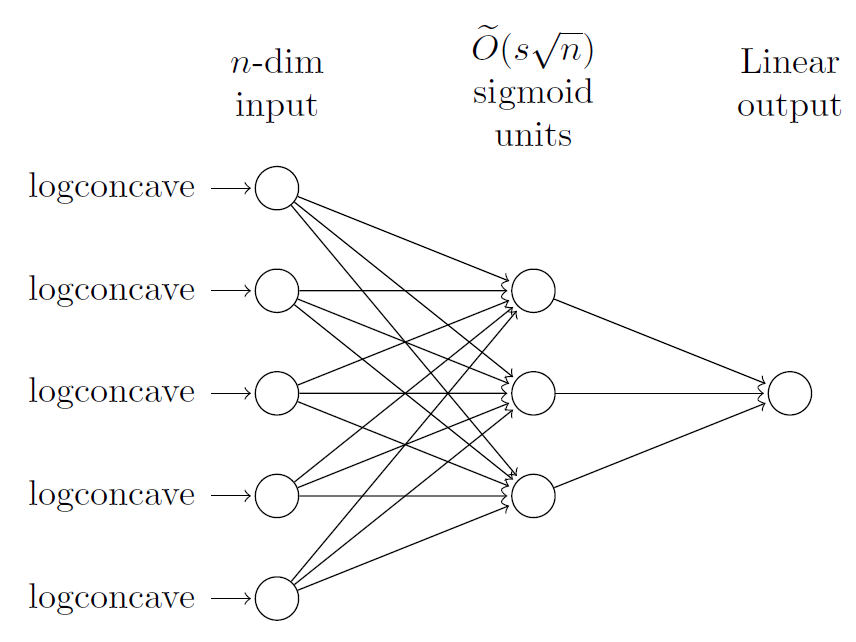
データを生成するNN
おのおのの入力次元について、i.i.dで[0,1]の実数値が入力されて、複雑なデータが生成される。
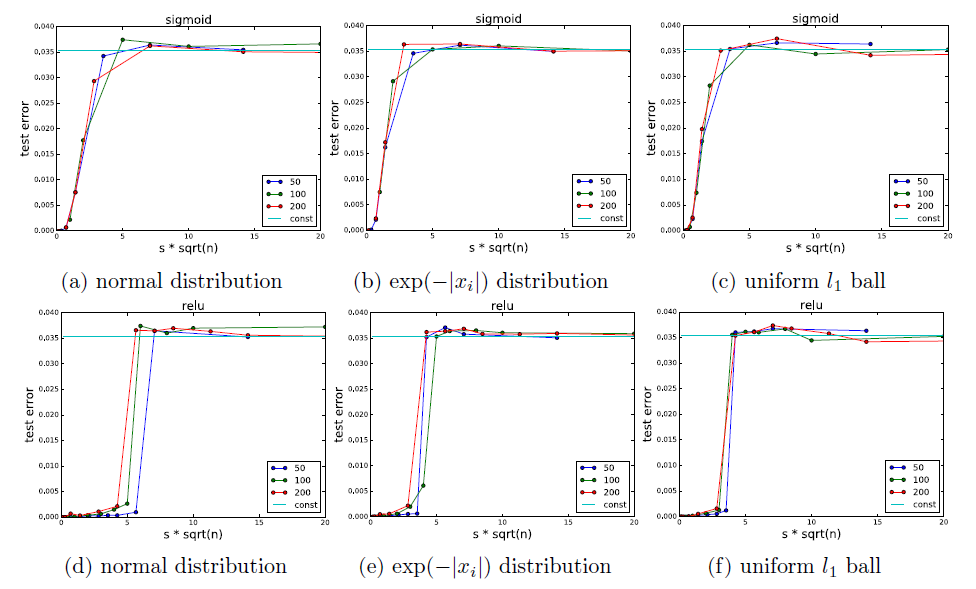
実験
理論上のテスト誤差の限界が緑の線です。ユニット数がある大きさになると、急激に学習ができなくなることが見て取れます!