【Unity2D】2点間の角度を求める

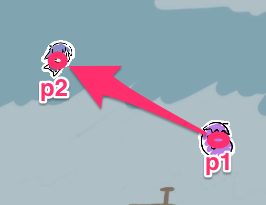
シューティングゲームでは必須となる狙い撃ち弾の角度の求め方です。

// p2からp1への角度を求める
// @param p1 自分の座標
// @param p2 相手の座標
// @return 2点の角度(Degree)
public float GetAim(Vector2 p1, Vector2 p2) {
  float dx = p2.x - p1.x;
  float dy = p2.y - p1.y;
  float rad = Mathf.Atan2(dy, dx);
  return rad * Mathf.Rad2Deg;
}

これで狙い撃ち弾を撃てるようになりました。

Vector2.Angleを使う

(2014/7/27 追記)
コメント欄で指摘頂いたのですが、Vector2.Angleという便利な関数があるので、それを使えば三角関数は不要になりそうです。

• Vector2.Angleの起点は、(0.0)です
  • http://d.hatena.ne.jp/shoji_hibino/20130531/1369973246

ただし、上記ページにあるように使用するには若干のクセがあるので注意が必要そうです。

仕様から察するに、たぶんこんな書き方で動くはず……。

// p2からp1への角度を求める
// @param p1 自分の座標
// @param p2 相手の座標
// @return 2点の角度(Degree)
public float GetAim(Vector2 p1, Vector2 p2) {
  Vector2 a = new Vector2(1, 0);
  Vector2 b = p2 - p1; // p1を原点に持ってくる
  return Vector2.Angle(a, b);
}

(2014/8/6 追記)
どうやらVector2.Angleは差を求めるだけなので、狙い撃ちの角度を取得するのには使えなさそうな感じです。

おまけ

取得した角度を元に rigidbody2Dに速度を設定する方法です

Bullet.cs

  // 速度を設定
  // @param 角度
  // @param 速さ
  public void SetVelocityForRigidbody2D(float direction, float speed) {
    // Setting velocity.
    Vector2 v;
    v.x = Mathf.Cos (Mathf.Deg2Rad * direction) * speed;
    v.y = Mathf.Sin (Mathf.Deg2Rad * direction) * speed;
    rigidbody2D.velocity = v;
  }

おまけ2

狙い撃つ相手を探すために GameObject.Find() や GameObject.FindWithTag() を使用することになると思いますが、この関数は全オブジェクトを走査することとなるため、弾幕STGのようなオブジェクトが大量にあるゲームでは処理が重くなります。そのため以下のようにキャッシュさせて使用すると処理を軽くすることができます。（ただしPlayerは1つのみであることが前提)

Enemy.cs

  // キャッシュ用変数
  private GameObject _target = null;

  // 狙い撃ち角度を取得する
  public float GetAim() {
    if(_target == null) {
      // 未取得であればキャッシュする
      _target = GameObject.FindWithTag ("Player");
    }
    Vector2 p1 = transform.position;
    Vector2 p2 = _target.transform.position;
    float dx = p2.x - p1.x;
    float dy = p2.y - p1.y;
    float rad = Mathf.Atan2(dy, dx);

    return rad * Mathf.Rad2Deg;
  }