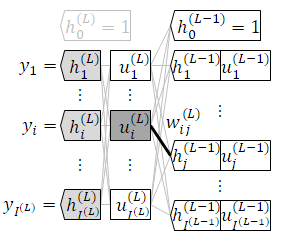なるべく簡単な数学で、ニューラルネットワークの数学を確認します。
入力値 $(x_1, x_2, x_3, \cdots x_{I^{(0)}})$ に対する 目標値 $(t_1, t_2, \cdots , t_{I^{(L)}})$ のデータ $N$ 件が与えられているとします。
ニューラルネットワークは入力値から 出力値 $(y_1, y_2, \cdots , y_{I^{(L)}})$ を計算し、出力値が目標値のよい近似になることを目指します。
\require{cancel}
\begin{bmatrix} t_1 \\ t_2 \\ \vdots \\ t_{I^{(L)}} \end{bmatrix} \quad
\Leftrightarrow \quad \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_{I^{(L)}} \end{bmatrix}
= \boxed{\begin{array}{c} \\ \\ \qquad \text{ニューラルネットワーク} \qquad \\ \\ \\ \end{array}} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_{I^{(0)}} \end{bmatrix} \\
ニューラルネットワークの構造
ノード
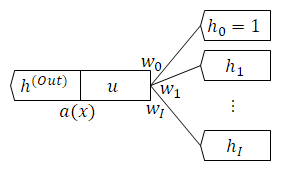
ニューラルネットワークの最小の構成要素は ノード です。
入力値の組 $(h_1, h_2, \cdots , h_I)$ に $h_0 = 1$ を追加した $(h_0, h_1, h_2, \cdots , h_I)$ から出力値 $h^{(Out)}$ を計算します。
ノード自体は各入力値の 重み付け $(w_0, w_1, w_2, \cdots , w_I)$ と 活性化関数 $a(x)$ を持ちます。
計算は次の $2$ 段階です。
\begin{array}{lc}
1. & u = w_0 h_0 + w_1 h_1 + w_2 h_2 + \cdots + w_j h_j + \cdots + w_I h_I \\
2. & h^{(Out)} = a(u) \\
\end{array}
今回は活性化関数にReLU (正規化線形関数) を用います。
関数と微分を示します。
\begin{array}{ccccc}
a(u) &=& \text{max}(u,0) &=& \left\{ \begin{array}{lc} 0 & (u \lt 0) \\ u & (0 \leq u) \\ \end{array} \right. \\
a'(u) &=& \displaystyle{ \frac{\partial}{\partial u} a(u) } &=& \left\{ \begin{array}{lc} 0 & (u \lt 0) \\ 1 & (0 \leq u) \\ \end{array} \right. \\
\end{array}
層
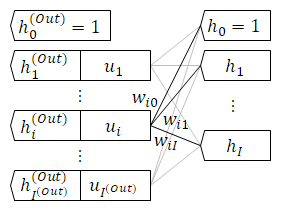
層 はノードを複数集めたものです。
同じ層のノードは入力値の組 $(h_0, h_1, h_2, \cdots , h_I)$ と活性化関数 $a(x)$ は同じです。
一方、重み付けはノードで異なります。
$i$ 番目のノードが持つ重み付けを $(w_{i0}, w_{i1}, w_{i2} , \cdots , w_{ij} , \cdots , w_{iI})$ と書きます。
$w_{ij}$ は $i$ 番目のノードが受け取る $j$ 番目の入力値の重みです。
層全体では入力値の組から出力値の組 $(h_1^{(Out)}, h_2^{(Out)}, \cdots , h_{I^{(Out)}}^{(Out)} )$ を返します。
ここでも出力値に $h_0^{(Out)} = 1$ を追加します。
ニューラルネットワーク
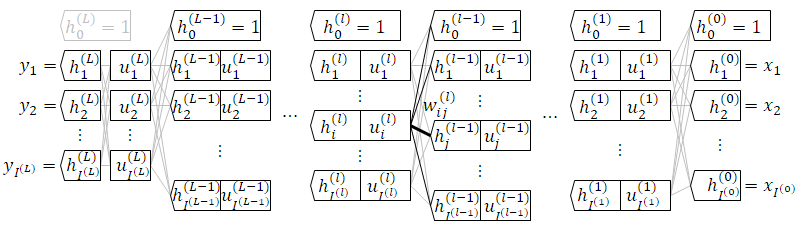
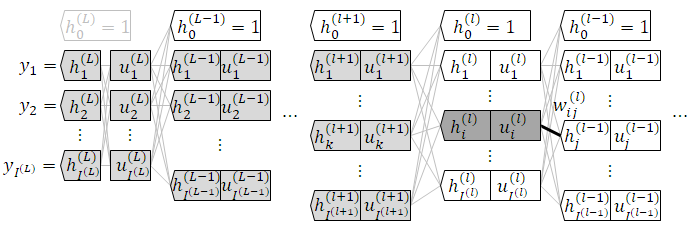
ニューラルネットワークは層を重ねた構造です。
前の層の出力が、次の層の入力です。
最初を 入力層 (第 $0$ 層) 、最後を 出力層 (第 $L$ 層) 、間を 中間層 (第 $l$ 層) または 隠れ層 と呼びます。
変数の表記を整理します。
層番号は変数右肩にかっこ書き、着目する層のノード番号は $i$ 、前の層のノード番号は $j$ とします。
\begin{array}{ccl}
w_{ij}^{(l)} & : & \text{ 第 } l \text{ 層の } i \text{ 番目のノードが、 } 1 \text{ つ前の層の } j \text{ 番目のノードから受け取る値の重み付け } \\
u_i^{(l)} & : & \text{ 第 } l \text{ 層の } i \text{ 番目のノードが計算した入力値の重み付けの和 } \\
h_i^{(l)} & : & \text{ 第 } l \text{ 層の } i \text{ 番目のノードの出力値 } \\
\end{array}
順伝播の数式
入力層
\begin{array}{lc}
1. & \cancel{ \phantom{ aaaaaaaa } } & \\
2. & h_0^{(0)} = 1 \quad , \quad h_i^{(0)} = x_i \\
\end{array}
中間層
\begin{array}{lc}
1. & u_i^{(l)} = w_{i0}^{(l)} h_0^{(l-1)} + w_{i1}^{(l)} h_1^{(l-1)} + \cdots + w_{ij}^{(l)} h_j^{(l-1)} + \cdots + w_{iI^{(l-1)}} h_{I^{(l-1)}}^{(l-1)} \\
2. & h_0^{(l)} = 1 \quad , \quad h_i^{(l)} = a(u_i^{(l)}) \\
\end{array}
出力層
\begin{array}{lc}
1. & u_i^{(L)} = w_{i0}^{(L)} h_0^{(L-1)} + w_{i1}^{(L)} h_1^{(L-1)} + \cdots + w_{ij}^{(L)} h_j^{(L-1)} + \cdots + w_{iI^{(L-1)}}^{(L)} h_{I^{(L-1)}}^{(L-1)} \\
2. & \cancel{ h_0^{(L)} = 1 } \quad , \quad h_i^{(L)} = a_i^{(L)}(u_1^{(L)}, u_2^{(L)}, \cdots , u_i^{(L)} , \cdots , u_{I^{(L)}}^{(L)}) \\
\end{array}
入力値の組から出力値の組を計算することを 順伝播 と呼びます。
出力層に $h_0^{(L)} = 1$ は追加しません。
出力層の活性化関数 $a_i^{(L)}(\cdots)$ は問題に応じて中間層とは異なる関数を使います。
$a_i^{(L)}(\cdots)$ は一般的にすべての $u_i^{(L)}$ の関数です。
$h_i^{(L)}$ はニューラルネットワークの最終的な出力値で、冒頭の $y_i$ と同じものです。
目的関数
出力値の組 $(y_1, y_2, \cdots , y_{I^{(L)}})$ と目標値の組 $(t_1, t_2, \cdots, t_{I^{(L)}})$ の不一致さを 目的関数 $L$ で定量化します。
出力値が目標値に近いほど $L$ は小さくなります。
L = L(y_1, y_2, \cdots , y_{I^{(L)}}, t_1, t_2, \cdots, t_{I^{(L)}}) \\
ニューラルネットワークの最適化
中間層の層の数とノード数、目的関数と出力層の活性化関数の具体形を与えれば、ニューラルネットワークの変数は $w_{ij}^{(l)}$ のみです。
$w_{ij}^{(l)}$ に乱数で値を与えれば、$1$ 件の入力値の組から $1$ 件の出力値の組を得て、目的関数が計算できます。
ここで偏微分値 $\frac{\partial L}{\partial w_{ij}^{(l)}}$ が計算できたとします。
この偏微分値は $w_{ij}^{(l)}$ を微小変化させたときの $L$ の増加の度合いです。
偏微分値と逆方向に $w_{ij}^{(l)}$ を微小変化させれば $L$ の減少が見込めます。
$$
w_{ij}^{(l)} \leftarrow w_{ij}^{(l)} - r \cdot \frac{\partial L}{\partial w_{ij}^{(l)}}
$$
$r$ を 学習率 と呼びます。
改善のきめ細かさを決める小さな正の数です。
誤差逆伝播の導出
$w_{ij}^{(l)}$ の改善式を微分の連鎖律を用いて確認します。
出力層
\begin{align}
w_{ij}^{(L)} & \leftarrow w_{ij}^{(L)} - r \cdot \frac{\partial L}{\partial w_{ij}^{(L)}} \\
& = w_{ij}^{(L)} - r \cdot \frac{\partial L}{\partial u_i^{(L)}} \cdot \frac{\partial u_i^{(L)}}{\partial w_{ij}^{(L)}} \\
& = w_{ij}^{(L)} - r \cdot \boxed{ \frac{\partial L}{\partial u_i^{(L)}} } \cdot h_j^{(L-1)} \\
\end{align}
\because \frac{\partial u_i^{(L)}}{\partial w_{ij}^{(L)}} = \frac{\partial}{\partial w_{ij}^{(L)}} (w_{i0}^{(L)} h_0^{(L-1)} + w_{i1}^{(L)} h_1^{(L-1)} + \cdots + w_{ij}^{(L)} h_j^{(L-1)} + \cdots + w_{iI^{(L-1)}} h_{I^{(L-1)}}^{(L-1)}) = h_j^{(L-1)}
中間層
\begin{align}
w_{ij}^{(l)} & \leftarrow w_{ij}^{(l)} - r \cdot \frac{\partial L}{\partial w_{ij}^{(l)}} \\
& = w_{ij}^{(l)} - r \cdot \frac{\partial L}{\partial u_i^{(l)}} \cdot \frac{\partial u_i^{(l)}}{\partial w_{ij}^{(l)}} \\
& = w_{ij}^{(l)} - r \cdot \boxed{ \frac{\partial L}{\partial u_i^{(l)}} } \cdot h_j^{(l-1)} \\
& = w_{ij}^{(l)} - r \cdot \boxed{ \frac{\partial L}{\partial h_i^{(l)}} \cdot \frac{\partial h_i^{(l)}}{\partial u_i^{(l)}} } \cdot h_j^{(l-1)} \\
& = w_{ij}^{(l)} - r \cdot \boxed{ \sum_{k=1}^{I^{(l+1)}} \biggl( \frac{\partial L}{\partial u_k^{(l+1)}} \cdot \frac{\partial u_k^{(l+1)}}{\partial h_i^{(l)}} \biggr) \cdot \frac{\partial h_i^{(l)}}{\partial u_i^{(l)}} } \cdot h_j^{(l-1)} \\
& = w_{ij}^{(l)} - r \cdot \boxed{ \sum_{k=1}^{I^{(l+1)}} \biggl( \boxed{ \frac{\partial L}{\partial u_k^{(l+1)}} } \cdot w_{ki}^{(l+1)} \biggr) \cdot a'(u_i^{(l)}) } \cdot h_j^{(l-1)} \\
\end{align}
\because \frac{\partial u_k^{(l+1)}}{\partial h_i^{(l)}} = \frac{\partial}{\partial h_i^{(l)}} (w_{k0}^{(l+1)} h_0^{(l)} + w_{k1}^{(l+1)} h_1^{(l)} + \cdots + w_{ki}^{(l+1)} h_i^{(l)} + \cdots + w_{kI^{(l)}}^{(l+1)} h_{I^{(l)}}^{(l)}) = w_{ki}^{(l+1)} \\
\because \frac{\partial h_i^{(l)}}{\partial u_i^{(l)}} = \frac{\partial}{\partial u_i^{(l)}} \bigl( a(u_i^{(l)}) \bigr) = a'(u_i^{(l)}) \\
$3$ 行目までは出力層と同じ形です。
囲み枠に注目します。
中間層では $\frac{\partial L}{\partial u_i^{(l)}}$ が $1$ つ出力層側の $\frac{\partial L}{\partial u_k^{(l+1)}}$ で表されます。
起点となる出力層の $\frac{\partial L}{\partial u_i^{(L)}}$ を求めれば、連鎖的にすべての $\frac{\partial L}{\partial u_i^{(l)}}$ を計算可能です。
これを 誤差逆伝播 と呼びます。
誤差逆伝播(まとめ)
\begin{array}{cc}
\displaystyle{ w_{ij}^{(l)} \leftarrow w_{ij}^{(l)} - r \cdot \frac{\partial L}{\partial u_i^{(l)}} \cdot h_j^{(l-1)} } & (l = L, L-1, \cdots , 2, 1) \\
\displaystyle{ \frac{\partial L}{\partial u_i^{(l)}} = \sum_{k=1}^{I^{(l+1)}} \biggl( \frac{\partial L}{\partial u_k^{(l+1)}} \cdot w_{ki}^{(l+1)} \biggr) \cdot a'(u_i^{(l)}) } & (l = \phantom{L,} L-1, \cdots, 2, 1) \\
\end{array}
起点となる出力層の $\frac{\partial L}{\partial u_i^{(L)}}$ は陽に求める必要があります。
$1$ 回の誤差逆伝播は $w_{ij}^{(l)}$ の微小な改善です。
最適化が完了するまで $N$ 件のデータに対して繰り返し適用します。
回帰問題への適用
出力層の活性化関数に 恒等関数 を、目的関数に 二乗誤差 を使います。
h_i^{(L)} = a^{(L)}_i(u_1, u_2, \cdots , u_i , \cdots , u_{I^{(L)}}) = a^{(L)}(u_i^{(L)}) = u_i^{(L)} \\
L = (h_1^{(L)} - t_1)^2 + \cdots + (h_i^{(L)} - t_i)^2 + \cdots + (h_{I^{(L)}}^{(L)} - t_{I^{(L)}})^2 \\
誤差逆伝播の起点 $\frac{\partial L}{\partial u_i^{(L)}}$ を陽に計算します。
\begin{align}
\frac{\partial L}{\partial u_i^{(L)}}
& = \frac{\partial L}{\partial h_i^{(L)}} \cdot \frac{\partial h_i^{(L)}}{\partial u_i^{(L)}} \\
& = \frac{\partial}{\partial h_i^{(L)}} \bigl( (h_1^{(L)} - t_1)^2 + \cdots + (h_i^{(L)} - t_i)^2 + \cdots + (h_{I^{(L)}}^{(L)} - t_{I^{(L)}})^2 \bigr) \cdot \frac{\partial}{\partial u_i^{(L)}} a^{(L)}(u_i^{(L)}) \\
& = \frac{\partial}{\partial h_i^{(L)}} \bigl( (h_i^{(L)} - t_i)^2 \bigr) \cdot \frac{\partial}{\partial u_i^{(L)}} u_i^{(L)} \\
& = \frac{\partial}{\partial h_i^{(L)}} \bigl( (h_i^{(L)})^2 - 2 h_i^{(L)} t_i + t_i^2 \bigr) \cdot 1 \\
& = 2 h_i^{(L)} - 2 t_i \\
& = 2 (h_i^{(L)} - t_i)
\end{align}
分類問題への適用
目標値 $(t_1, t_2, \cdots , t_{I^{(L)}})$ が ワン ホット ベクトル で与えられているとします。
出力層の活性化関数に ソフトマックス関数 を、目的関数に クロスエントロピー を使います。
h_i^{(L)} = a^{(L)}_i(u_1, u_2, \cdots , u_i , \cdots , u_{I^{(L)}}) = \frac{e^{u_i}}{\sum_{k=1}^{I^{(L)}} e^{u_k}} \\
L = -t_1 \log{h_1^{(L)}} - \cdots - t_i \log{h_i^{(L)}} - \cdots - t_{I^{(L)}} \log{h_{I^{(L)}}^{(L)}} \\
誤差逆伝播の起点 $\frac{\partial L}{\partial u_i^{(L)}}$ を陽に計算します。
\begin{align}
\frac{\partial L}{\partial u_i^{(L)}}
& = \sum_{j=1}^{I^{(L)}} \frac{\partial L}{\partial h_j^{(L)}} \cdot \frac{\partial h_j^{(L)}}{\partial u_i^{(L)}} \\
& = \sum_{j=1}^{I^{(L)}} \biggl[ \frac{\partial}{\partial h_j^{(L)}} \Bigl( -t_1 \log{h_1^{(L)}} - \cdots - t_j \log{h_j^{(L)}} - \cdots - t_{I^{(L)}} \log{h_{I^{(L)}}^{(L)}} \Bigr) \biggr] \cdot \biggl[ \frac{\partial}{\partial u_i^{(L)}} \Bigl( \frac{e^{u_j^{(L)}}}{\sum_{k=1}^{I^{(L)}} e^{u_k^{(L)}}} \Bigr) \biggr] \\
& = \sum_{j=1}^{I^{(L)}} \biggl[ \frac{\partial}{\partial h_j^{(L)}} \Bigl( -t_j \log{h_j^{(L)}} \Bigr) \biggr] \cdot \biggl[ \frac{\partial}{\partial u_i^{(L)}} \frac{f}{g} \biggr] \qquad \qquad (f = e^{u_j^{(L)}} \quad , \quad g = \textstyle{ \sum_{k=1}^{I^{(L)}} e^{u_k^{(L)}} } ) \\
& = \sum_{j=1}^{I^{(L)}} \biggl[ \frac{-t_j}{h_j^{(L)}} \biggr] \cdot \biggl[ \frac{1}{g^2} \Bigl( f'g - fg' \Bigr) \biggr] \\
& = \sum_{j=1}^{I^{(L)}} \biggl[ \frac{-t_j}{h_j^{(L)}} \biggr] \cdot \biggl[ \frac{1}{(\sum_{k=1}^{I^{(L)}} e^{u_k^{(L)}})^2} \Bigl( \frac{\partial}{\partial u_i^{(L)}} \bigl( e^{u_j^{(L)}} \bigr) \cdot \sum_{k=1}^{I^{(L)}} e^{u_k^{(L)}} - e^{u_j^{(L)}} \cdot \frac{\partial}{\partial u_i^{(L)}} \bigl( \sum_{k=1}^{I^{(L)}} e^{u_k^{(L)}} \bigr) \Bigr) \biggr] \\
& = \sum_{j=1}^{I^{(L)}} \biggl[ \frac{-t_j}{h_j^{(L)}} \biggr] \cdot \biggl[ \frac{1}{(\sum_{k=1}^{I^{(L)}} e^{u_k^{(L)}})^2} \Bigl( \delta_{ij} e^{u_j^{(L)}} \cdot \sum_{k=1}^{I^{(L)}} e^{u_k^{(L)}} - e^{u_j^{(L)}} \cdot e^{u_i^{(L)}} \Bigr) \biggr] \qquad \qquad \biggl( \delta_{ij} = \left\{ \begin{array}{ll} 1 & (i = j) \\ 0 & (i \neq j) \end{array} \right. \biggr) \\
& = \sum_{j=1}^{I^{(L)}} \biggl[ \frac{-t_j}{h_j^{(L)}} \biggr] \cdot \biggl[ \delta_{ij} \cdot \frac{e^{u_j^{(L)}}}{\sum_{k=1}^{I^{(L)}} e^{u_k^{(L)}}} - \frac{e^{u_j^{(L)}}}{\sum_{k=1}^{I^{(L)}} e^{u_k^{(L)}}} \cdot \frac{e^{u_i^{(L)}}}{\sum_{k=1}^{I^{(L)}} e^{u_k^{(L)}}} \biggr] \\
& = \sum_{j=1}^{I^{(L)}} \biggl[ \frac{-t_j}{h_j^{(L)}} \biggr] \cdot \biggl[ h_j^{(L)} (\delta_{ij} - h_i^{(L)}) \biggr] \qquad \qquad \because h_i^{(L)} = \frac{e^{u_i^{(L)}}}{\sum_{k=1}^{I^{(L)}} e^{u_k^{(L)}}} \\
& = \sum_{j=1}^{I^{(L)}} t_j (h_i^{(L)} - \delta_{ij}) \\
& = h_i^{(L)} \sum_{j=1}^{I^{(L)}}t_j - \sum_{j=1}^{I^{(L)}} \delta_{ij} t_j \\
& = h_i^{(L)} - \sum_{j=i}^{i} t_j \qquad \qquad \because (t_1, t_2, \cdots , t_{I^{(L)}}) \text{ is a one hot vector.} \\
& = h_i^{(L)} - t_i \\
\end{align}