おはようございます。今日も一日リモート日和
今回は2020年4月12日にAtCoderで開催されたAtCoder Beginner Contest 162のE問題について書きます。
この問題はいくつか解法があって、計算量もそれぞれ違います。
高速化パートはまだ書けていません!ごめんなさい 書きあがったらここに→←ここにリンクを入れます
AtCoder Beginner Contest 162 E問題「Sum of gcd of Tuples (Hard)」
$1$ 以上 $K$ 以下の整数からなる長さ $N$ の数列 $\{A_1,\ldots,A_N\}$ を考えます。
そのようなものは $K^N$ 個ありますが、その全てについての $\gcd(A_1,\ldots,A_N)$ の和を求めてください。
ただし、答えは非常に大きくなる可能性があるため、和を $(10^9+7)$ で割ったあまりを出力してください。
なお、$\gcd(A_1,\ldots,A_N)$ は $A_1,\ldots,A_N$ の最大公約数を表します。
(コンテスト問題ページから引用)
たとえば、$K=3,N=2$ とすると、ありえる数列は $(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)$ です。それぞれ最大公約数は $1,1,1,1,2,1,1,1,3$ で、合計は $12$ です。
解法
数列すべてについて毎回最大公約数を計算していると、計算量は $O(K^N(N+\log K))$ 程度になってしまい、$N=K=10^5$ の最大ケースではまったく間に合いません。
なので、なんとかして処理をまとめてしまわないといけません。どの要素に着目してまとめるかによって解法に幅が出ます。
- 長さが $N$ で $1$ 以上 $k$ 以下の整数からなる数列のうち、 $\gcd$ が $1$ になるようなものの個数 $f_N(k)$
- $K^N$ 個の数列すべてのうち、$\gcd$ が $n$ の倍数になるものの個数 $\lfloor K/n\rfloor^N$
- 数学的な式変形をさらに繰り返してがんばる
以下でそれぞれ詳しく解説します。
(公式の解説は解法2で書かれています)
解法 1
解法1では、「長さが $N$ で $1$ 以上 $k$ 以下の整数からなる数列のうち、 $\gcd$ が $1$ になるようなものの個数 $f_N(k)$」を求めて、さらにこれを利用して答えを求めます。
これを一発でぱーんと求めてしまうのは難しそうなので、$k$ の小さいほうから順番に求めていくことを考えます。
今、$k'<k$ が成り立つような $k'$ については好きに $f_N(k')$ の値を参照していいとします。このとき、$f_N(k)$ は
\begin{equation}\begin{split}
f_N(k)&=\left(\text{数列全体の個数}\right)-\left(\gcd\text{が }1\text{ より大きい数列の個数}\right)\\
&=\left(\text{数列全体の個数}\right)-\sum_{i=2}^k\left(\gcd\text{が }i\text{ である数列の個数}\right)
\end{split}\end{equation}
と計算できます。
数列全体の個数は $k^N$ 個と簡単に求めることができます。$\gcd$ が $i$ である数列の個数はすぐに求められるでしょうか。
求められます!
「$\gcd$ が $i$ である数列」の全部の項を $i$ で割ってしまうことで、「長さが $N$ で、 $1$ 以上 $\lfloor k/i\rfloor$ 以下の整数からなる $\gcd$ が $1$ の数列」と一対一に対応させることができます。

なので、結局 $f_N(k)$ はこう書くことができます。
f_N(k)=k^N-\sum_{i=2}^kf_N\left(\left\lfloor\dfrac{k}{i}\right\rfloor\right)
これを愚直に下から計算していくと $O(K^2+K\log N)$ 時間かかってしまいますが、上からメモ化しながら必要なところだけ計算すると、$O(K(\log K+\log N))$ 時間で $f_N(K)$ を求められます(下の方で全体の計算量見積もりと一緒に証明します)。
$f_N(K)$ を求められたので、これを利用して答えを求めたいです。しかし今やそれはとても簡単です!
上で確認したように、列全体を最大公約数で割ることで「要素が $1$ 以上 $K$ 以下で $\gcd$ が $i$ である列」と「要素が $1$ 以上 $\lfloor k/i\rfloor$ 以下で $\gcd$ が $1$ である列」を一対一対応させることができます。なので、答えは
\begin{equation}\begin{split}
&\sum_{i=1}^ki\times\left(\gcd\text{が }i\text{ である数列の個数}\right)\\
=&\sum_{i=1}^ki\times f_N\left(\left\lfloor\dfrac{k}{i}\right\rfloor\right)
\end{split}\end{equation}
と計算できます。全体の計算時間は $O(K(\log K+\log N))$ です。
C++でACする実装はこちらです。
計算時間見積もり
必要なところだけメモ化すると $O(K(\log K+\log N))$ とか、$f_N(\lfloor k/i\rfloor)$ を全部求めても計算量が変わらないとか非自明な事実があります。詳しく考えていきましょう。
重要事実 1
まず、次の重要な事実を証明します。
実は、$f_N(k)$ を計算するときには、$f_N(\lfloor k/i\rfloor)$ の形でしか $f_N$ を必要としません。
???「式の形から自明じゃん」
f_N(k)=k^N-\sum_{i=2}^kf_N\left(\left\lfloor\dfrac{k}{i}\right\rfloor\right)
いいえ!たとえば、この式を計算するのに使う $f_N(\lfloor k/2\rfloor)$ の値を決めるために必要な $f_N$ も上の形になっていることは少し議論が必要です。
では議論をしましょう。もう少し強く、以下を示せば十分です(整数と整数をかけても整数)。
\left\lfloor\dfrac{\lfloor k/i\rfloor}{j}\right\rfloor=\left\lfloor\dfrac{k}{ij}\right\rfloor
$\lfloor k/i\rfloor=n,\lfloor n/j\rfloor=m$ とおきます。示すべきことは、$ni\leq k<(n+1)i,mj\leq n<(m+1)j$ のもとで $mij\leq k<(m+1)ij$ が成り立つことと言い換えられます。
第二式を $i>0$ 倍することで $mij\leq ni\leq k<(n+1)i\leq(m+1)ij$ が示されました。 おしまい。
以上より、$f_N(k)$ を計算するときには $f_N(\lfloor k/i\rfloor)$ の形でしか $f_N$ を使わないことがわかりました。逆に、$f_N(k)$ の計算には $f_N(\lfloor k/i\rfloor),i>1$ の形の全てが必要です(こちらは本当に「式形から明らか」です)。
本編
この事実が証明されたので、
- $f_N(K)$ さえ計算すれば、残りのパートで必要とする値は全て計算されているということ
- $f_N(K)$ を計算する際には、$f_N(\lfloor K/i\rfloor)$ 以外の値は使わないこと
がわかりました。
よって、$\lfloor K/i\rfloor$ の小さいほうから $f_N$ を計算するとしてしまってもかまいません。
再帰先がすべて計算されているなら、$f_N(k)$ の計算は $O(\log N+k)$ 時間しか必要としません。なので、全体の計算時間は
\begin{equation}\begin{split}
&\sum_{i=1}^K\left(f_N\left(\left\lfloor\dfrac{K}{i}\right\rfloor\right)\text{の計算にかかる時間}\right)\\
=&\sum_{i=1}^K\left(\log N+\left\lfloor\dfrac{K}{i}\right\rfloor\right)=O(K\log N+K\log K)
\end{split}\end{equation}
と見積もることができます。ここで、$\dfrac{1}{1}+\cdots+\dfrac{1}{n}=O(\log n)$を利用しました。足したり引いたりするのは $O(K)$ 回なので、全体で計算時間は $O(K(\log K+\log N))$ と見積もることができます。おしまい ハッピーです 何か不明瞭だったりわからないところがあったら質問をください
解法 2
解法2では、「$K^N$ 個の数列すべてのうち、$\gcd$ が $n$ の倍数になるものの個数が $\lfloor K/n\rfloor^N$ 個」であるところから出発して、答えを求めます。
$\gcd$ がちょうど $n$ になるような数列の個数を $v(n)$ と書くことにします。 すると、
\sum_{n|m}v(m)=\left(\gcd\text{が }n\text{ の倍数になる数列の個数}\right)=\left\lfloor\frac{K}{n}\right\rfloor^N
となります。
ところでいっぱい勉強をしている競技プログラマの人はわかるかもしれません、ここで8割がた解けています。
約数集合によるゼータ変換/約数包除
約数集合でのゼータ変換・メビウス変換的なやつと畳み込み
高速ゼータ変換の約数版 O(N log(log(N)))
私の説明がわかりにくかったら↑などを読んでみてください
包除原理ならぬ除原理と呼ばれていたりもします。
\sum_{n|m}g(m)=f(n)
なる関数 $f,g$ を相互に変換したり、あるいは $\displaystyle\sum_{d|n}g(d)=f(n)$ なる $f,g$ を相互に変換するのが高速にできますよ、という話です。
もう少し正確な書き方をすると、「上の式を満たすような $g$ について、$g(1),\ldots,g(N)$ の値から $f(1),\ldots,f(N)$ の値を計算する」ことが、愚直にしたら時間計算量が $O(N\log N)$ のところ、$O(N\log\log N)$ でできます ということです。
愚直に
そもそもこれに $O(N\log N)$ かけても元の問題は解けていますね( $O(K(\log K+\log N))$ になります) まずはこの方法を説明します。
$n\leq K<2n$ のとき、「$\gcd$ が $n$ の倍数」$\iff$「$\gcd$ が $n$」です( $\gcd$ は数列のどの要素よりも大きくなれないので)。
つまり、そこでは $v(n)=\lfloor K/n\rfloor$ が成り立っています。
$2n\leq K<3n$ のとき、「$\gcd$ が $n$ の倍数」$\iff$「$\gcd$ が $n$」か、「$\gcd$ が $2n$」です。後者の数である $v(2n)$ は上で正しい値が求められていたので、$v(n)$ も正しく求められます。
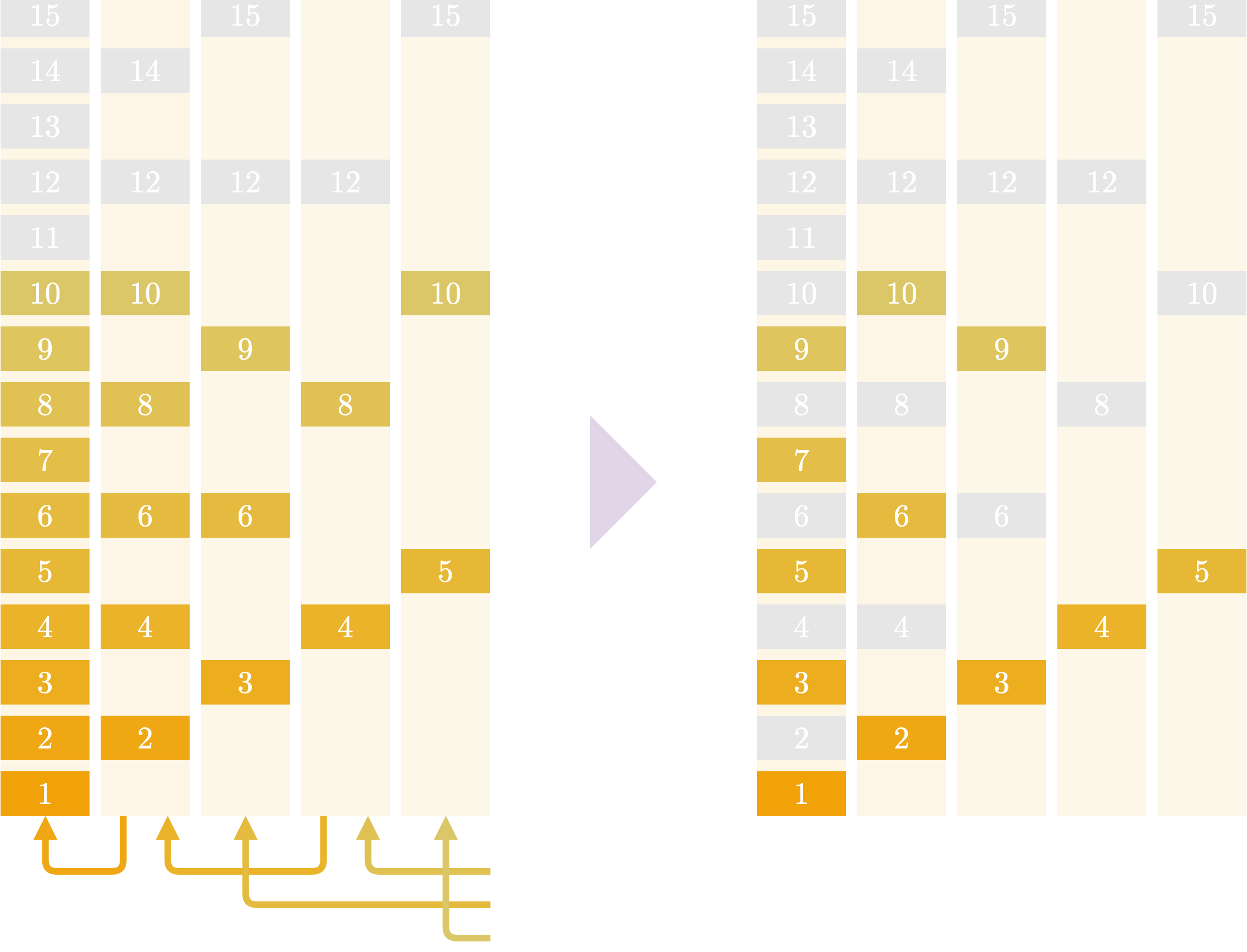
$K=10$ とした模式図を書くと、こんなかんじです
上は $f(n)$ 、倍数全体の和を表しています。$K$ より大きいところは灰色にしてあります。
大きい矢印の順番に $v(n)$ を求めていきます。 $v(10),v(9),v(8),v(7),v(6)$ はそのまま、$v(5)$ を求めるときにはもう $v(10)$ が求まっているので $v(10)$ を引くだけで答えが求められます。
このようにして、$n$ の大きいほうから値を決めていくことで計算をすることができます。計算にかかる時間は $O(\sum_{n=1}^{K}\lfloor K/n\rfloor)=O(K\log K)$ です。
実装する際は $v[i]$ を最初すべて $\lfloor K/n\rfloor^N$ にしておくと楽です。
$\lfloor K/n\rfloor^N$ たちを求めるところで $O(K\log N)$ 、$v[i]$ を求めるところで $O(K\log K)$ 、あわせて $O(K(\log K+\log N))$ となります。
C++でACする実装はこちらです。
高速に
高速にできるなら高速にしたいですよね そうでもないですか? とりあえずこの操作は $O(K\log\log K)$ 時間で実現できます。
したい操作は、「はじめすべて $v[n]=f(n)$ で初期化された配列をなんとかして『 $v[n]$ から最終的な $v[kn]$ の値をすべて引い』て、$v[n]=g(n)$ にする」です。
はじめのうち $v[n]$ には倍数が合計された値が入っているので、あんまりいっぱい引かなくても目的の操作が達成されるかもしれないと思いませんか?実はできます。
まず、すべての $v[i]$ から $v[2i]$ を引きます( $i$ の小さいほうから計算します つまり、$v[2i]$ は古いほうの値を使います)。
すると、$v[2i]$ に入っていた $\sum g(2i$ の倍数$);=\sum g(i$ の偶数倍$)$ が引かれるので、今や $v[i]$ は $i$ の奇数倍についての $g(n)$ を引くだけでよくなります。
次に、$v[i]$ から $v[3i]$ を引くと、残りは(2でも3でも割り切れない数)倍だけになり、$v[5i]$ を引くと残りは(2でも3でも5でも割り切れない数)倍だけになり...
とすると、$p\leq K$ な素数 $p$ について $v[i]$ から $v[pi]$ を引くだけでしたかった操作ができることになります( $2$ 以上 $K$ 以下の整数は $K$ 以下の素数のいずれかで割り切れます)。
「引きすぎる」ことがないのを考えておきましょう。$v[i]$ から $v[pi]$ を引くとき、すでに $v[i]$ から引いたものは $g(qi)$ ($q$ は $p$ より小さい素因数をもつ) で、$v[pi]$ の中にそのようなものがないことを確認したいです。
ここで $v[pi]$ からはすべての $g(pqi)$ ($q$ は $p$ より小さい素因数をもつ) が引かれているので、$v[pi]$ には $g(ri)$ ($r$ は $p$ より小さい素因数をもたない) しか含まれていないことが示されました。
計算量の見積もりは少し難しいですが、$n$ 番目の素数 $p$ が $n\log n$ 程度であることと、素数定理$\pi(x)\sim\dfrac{x}{\log x}$を使うと、
\sum\dfrac{K}{n\log n}=O(K\log\log\pi(K))=O(K\log\log K)
と見積もることができます。
実装する際は素数の列挙と同時にすると綺麗で楽だと思います。
上と同様に、全体の時間計算量は $O(K(\log\log K+\log N))$ となります。
C++でACする実装はこちらです。
解法 3
解法3では、上2つの解法で出てきたような式をさらに変形してあまり難しいことを考えなくても実装して解けてしまえるようにします。
突然ですが、解法2でどのようなことをしたのか振り返ってみます。
解法2は、計算しやすいけれど数え過ぎてしまう式
\sum_{i=1}^Ki\left\lfloor\frac{K}{n}\right\rfloor^N
の「順列の個数」 $\lfloor K/n\rfloor$ の部分を調節して正しい答えを出すようにしました。
とても自然な考え方です。$\gcd$ が $2$ である数列はどう見ても $\gcd$ が $1$ である数列ではないのですから。
しかし、少しだけ不自然(でもとっても便利)な考え方をしてみましょう。
「順列の個数」ではなく「合計するものの大きさ」 $i$ のほうを調節する、と考えます。
これでも、合計は上と同じにできる気がします。$N$ や $K$ がもっと多いときにもこのような調節がうまくいくのでしょうか。実は、できます。
$\gcd$ が $i$ の列は、$i$ の全ての約数 $d$ について1回ずつ見られることになります。$\gcd$ が $d$ の倍数の列の合計するものの大きさを $f(d)$ に調節するとすると、次が成り立つような $f$ があればいいわけです。
\sum_{d|n}f(d)=n
あれ?これは上で見たような約数包除の形式をしています。
なので解法2で使ったようなテクニックを使えば解けますが、こんな綺麗な式ですから $f$ も綺麗かもしれないと思います 思いませんか? 思ったあなたは大正解で、これは有名な関数になります。
f(n)=\varphi(n):=(n\text{ 以下で }n\text{ と互いに素な正の整数の個数})\quad(\text{オイラーのトーシェント関数})
証明を詳しく書くことはしませんが、$\varphi(n/d)$ を「 $n$ 以下の正の整数 $m$ のうち $gcd(n,m)=d$ であるものの個数」と思うと示せます。
この $\varphi$ は有名な関数なので、計算の仕方も有名です。もしかしたらこれを計算するライブラリを持っている人もいるかもしれません。
具体的には、$n$ が異なる素数 $p_1,p_2,\ldots,p_k$ と正整数 $e_1,e_2,\ldots,e_k$ によって $n=p_1^{e_1}\cdots p_k^{e_k}$ と書けるとき、
\varphi(n)=n\prod_{i=0}^k\dfrac{p_i-1}{p_i}
です。
これは素因数分解さえできれば計算できます。
元の問題に戻ってくると、求めるものは結局
\sum_{i=1}^K\varphi(i)\left\lfloor\frac{K}{i}\right\rfloor^N
になりました。
$n$ の素因数分解は $O(\sqrt{n})$ 時間で、$N$ 乗は $O(\log N)$ 時間で実現できるので、全体の計算量は $O\left(K(\sqrt{K}+\log N)\right)$ になって、この問題が解けました。
C++でACする実装はこちらです。
高速化
について書こうと思ったんですけど、一旦ここで公開してしまいます(比較的難しくてニッチですし、そろそろコンテストから1週間も経ってしまいます) 書けたらここにリンクを張りますね
まとめ
私は別解がいくつもある問題が性癖なので、今回の問題はかなり好きな問題でした。
解法1はDPチックでメモ化で高速化で教育的な競技プログラミング感のある解法だと思います
解法2は私が本番で通した解法で、本質は解法1と似ていますけど、愚直にやっても速くて高速にするともっと早いです
解法3はすごいですよね 綺麗な式になって面白いです 組合せ論的な説明はあるんでしょうか? 組合せ論と式変形の海に身を投げる覚悟のある人なら一番実装が楽だと思います(もしかしたらほとんど貼るだけ?)
高速化パートは主に解法3の高速化を書く予定です。
こんな別解があるよ!ここがわかりにくいよ!などぜひぜひコメントしてください〜