2024/11/05 奈佐原顕郎
（書きかけです）
はじめに
合成開口レーダ（SAR）は人工衛星（JAXAのALOSシリーズやESAのSentinel-1シリーズなど）に搭載されて地球や惑星の表面を昼も夜も晴れでも曇りでもおかまいなしに高分解能で観測できるという, 魔法のようなテクノロジーです。その魔法を勉強しようとすると, SARのデータはそもそも複素数だという話にぶち当たります。なぜ複素数? それを本稿では説明しましょう。
なお, 電波工学ではそもそも電波を複素数で表すことが多いようですが, それは数学的な扱いをシンプルにするための便宜上のことであり, むしろそれが初心者を戸惑わせる一因のように私は思うので, 本稿では複素数の登場をできるだけ遅らせます。
1. SARの波長（周波数）は変動する
SARはアンテナから電波（マイクロ波）を地表面に向けて発射します。電波は電場（と磁束密度）が振動しながら空間を伝わる波です。波は上がったり下がったり（あるいは強くなったり弱くなったり）する現象ですから, その波の高さ（電場の強さ）は実数で表されます。だからSARから出る電波は実数（電場の強さ; 単位で言えばV/m）で表されます（上級者への注: ここでは偏波を考えません。特定の方向の直線偏光（直線偏波）に限定した話だと思ってください）。
電波（電磁波）といえば, 波長の短い（数nm）X線から波長の長いラジオ波（数100 m）までいろいろありますが, その中でSARが使うマイクロ波は, 波長が数 mmから数十 cmの電波です。このあたりの電波は「大気の窓」といって, 大気を通過することができます。しかも, 雲粒や塵に邪魔されないので, 雲や煙を透視できます。そういうわけで, 宇宙からの地球観測にぴったりなのです。
具体的にどの波長の電波を使うかは, 個々のSARシステムで決まっています。たとえばALOS-2/PALSAR-2は, 1257.5 MHzの周波数ですから, 波長（=光速/周波数）は23.84 cmです。ところが実際はこれより長い波長になったり短い波長になったりします。それは, PALSAR-2の周波数はいつもぴったり1257.5 MHzなのではなく, それを中心に84 MHzくらいの幅で増減するからです。これを帯域幅といいます（大事なキーワード！）。つまり, PALSAR-2の出す電波の周波数は, 時には1257.5 MHz - 84 MHz/2 = 1215.5 MHzだったり, 1257.5 MHz + 84 MHz/2 = 1299.5 MHzだったりします。1257.5 MHzはあくまでのその中心（中心周波数）です。波長で言えば, 23.07 cmから24.66 cmくらいの幅があるのです。
なぜ波長や周波数に幅がある（幅を持たせる）のでしょう? SARは出した電波が地表面に当たって跳ね返ってくるのを観測し, 往復の時間で距離を出すのですが, もしも波長や周波数が全く変動しないならば, それは正弦波（サインやコサインのカーブ）が延々と続くということです。同じようなパターンが延々と続く信号を地表に当てても, 戻ってくる信号は同じようなパターンが延々続くのですから, それがいつ地表に当たったのかがわからないのです。SARが意味のある観測をするには, 正弦波ではない, 何か特徴的なパターンを信号にしなければならないのです（正弦波の最初の部分が当たって跳ね返ったところを見ればよいだろう? と思うかもしれませんが, 正弦波には「最初」は無いのです。無限の昔から無限の将来まで周期的に続くのが正弦波であり, 正弦波の一部を切り出したものはもはや正弦波ではないのです）。シンプルな正弦波から少しでも違うパターンの波は, 複数の波長の波の重ね合わせとみなされます（フーリエ変換の考え方）から, 必然的に複数の波長（波長に幅のある波）を使うことになるのです。ただし, 以後の話は, このあたりがピンと来なくても大丈夫です。
2. チャープパルス
SARが地表に向けて発射する信号は数学的には以下のように「時刻$t$の2次関数の三角関数」であり, 「チャープパルス」と呼ばれます（より正確には, 次式は「パルス幅」と呼ばれる時間$\tau$について, $-\tau/2<t<τ/2$の間だけで成り立ち, それ以外では0）:
\cos(2\pi f t + \alpha t^2)\tag{1-1}
ここで$f$は中心周波数, $\alpha$は「チャープ率」という定数（SARシステムごとに決まっている）です。$\alpha$は0ではないのですが, もし仮に0なら$\cos 2\pi f t$となって, これはただのコサイン関数ですから正弦波です（正弦はもともとサインを意味するので, 「コサインなのに『正弦』って?」と思うかもしれませんが, コサインのグラフはサインのグラフを平行移動したものですので, サインもコサインも区別せずにまとめて「正弦波」というのです）。0でない$\alpha$があるがために, 式(1-1)は正弦波とは違った形になるのです。
ここで「位相」という言葉を定義しておきます。sinやcosのような周期的な関数において, その変数の部分を位相といいます。とくに, sin( )やcos( )のような関数の( )の中が位相です。
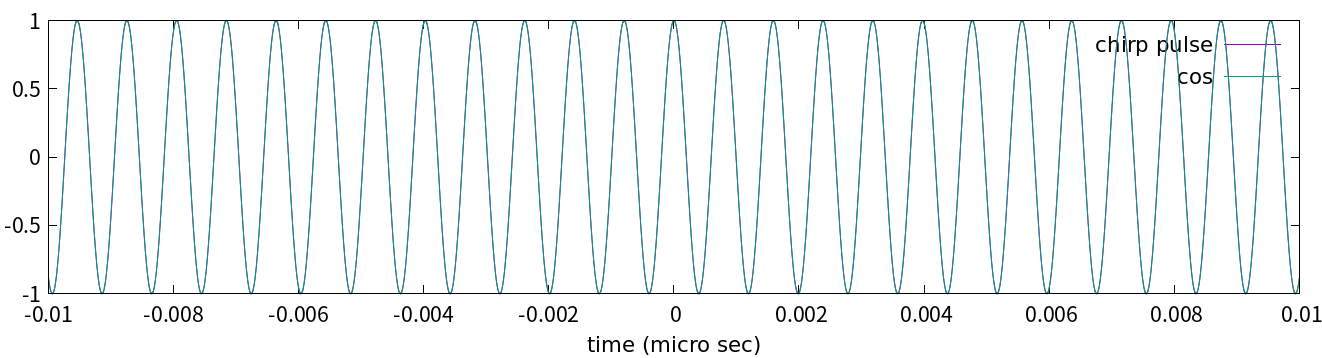
話を戻します。たとえば, PALSAR-2を想定して, $f$=1257.5 MHz, $\alpha$=5 MHz/μsのときの式(1-1)のグラフは以下のようになります:
図1-1: チャープパルスと搬送波（$t=0$付近）
ほとんど正弦波（コサイン）ですね（笑）。参考までに, $\alpha=0$のとき, つまり完全な正弦波もプロットしました。これを搬送波と呼びます（後で説明します）。チャープパルスと搬送波はぴったり重なってしまって区別がつきません。でもわずかに差があるのです。実際, 0.3μ秒ほど後の時刻ではこうなります:
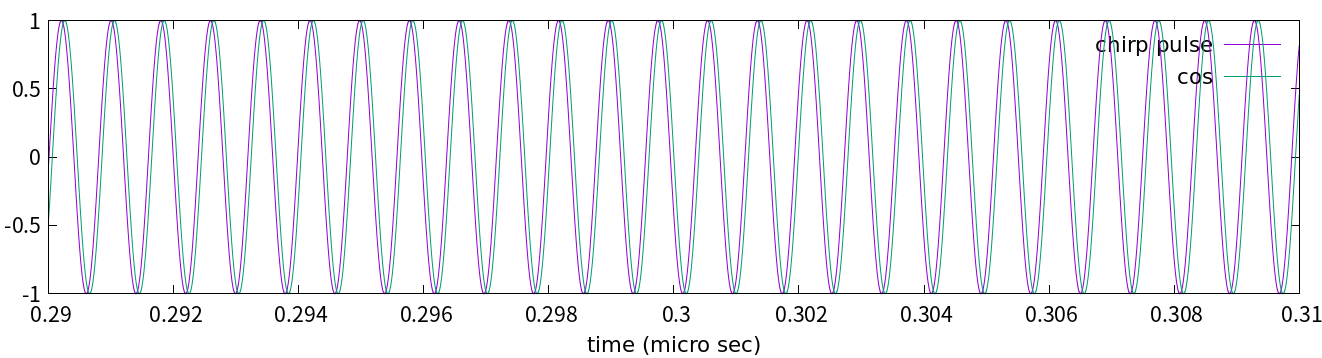
図1-2: チャープパルスと搬送波（$t=0$からちょっと離れたところ）
紫色がチャープパルス, 緑色が（チャープ率0の）正弦波（搬送波）です。時間の原点（パルスの中心）から離れるほど, チャープパルスはだんだん短くなっていくので, 正弦波からズレてくるのです。
さてここで, SARの勉強をしたことのある人は「私の知ってるチャープパルスとは違う!!」と思っているでしょう（そうでない人はそれでOKです）。そういう人は我慢して先を読んで下さい。
3. チャープパルスに正弦波を掛ける
今, 最も簡単なケースとして（現実性はともかく）, 距離0にあるターゲットが, SARから発射された信号をそのまま跳ね返す場合を考えましょう。つまり受信信号はこのチャープパルスとそっくり同じです。その信号は約1.3 GHz（正確には1257.5 MHzを中心に, 84MHzほど幅のある周波数）という, 周波数の高い信号です。1秒間にだいたい13億回も振動する信号です。しかしユーザーは, そんな高周波の信号をそのまま使うのではありません。実はこの信号に搬送波, つまり同じ中心周波数の正弦波（つまり$\alpha=0$）:
\begin{align}
\cos(2\pi f t)\tag{3-1}
\end{align}
を「掛け算」するのです。
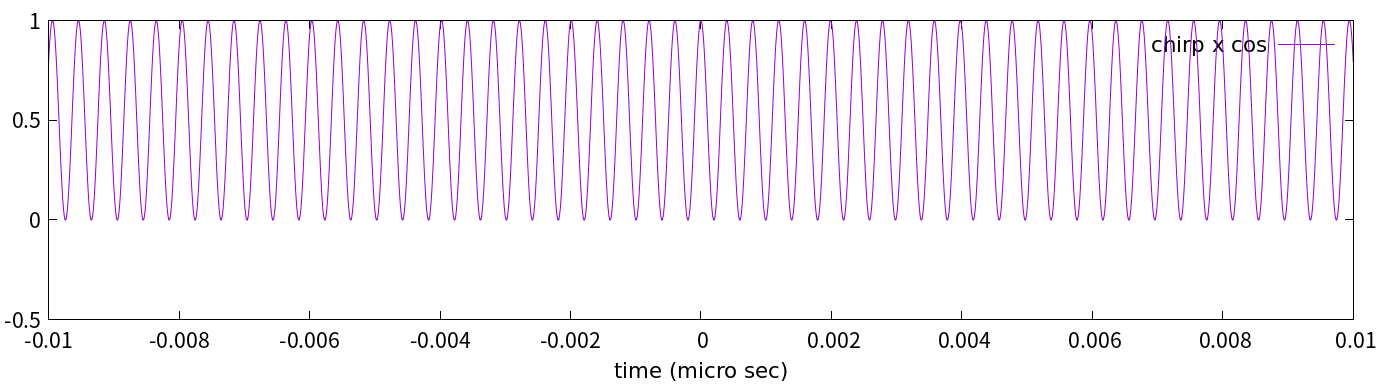
\cos(2\pi f t + \alpha t^2)\cos(2\pi f t)\tag{3-2}\\
すると, 以下のようなグラフになります:
図3-1
... ただの正弦波っぽいですね（笑）。これは$t$の範囲が狭いからそう見えているだけです。思い切って広く見てみましょう。PALSAR-2のパルス継続時間は20μ秒から40μ秒らしいので, その2割程度の±4μ秒間を見るとこうなります:
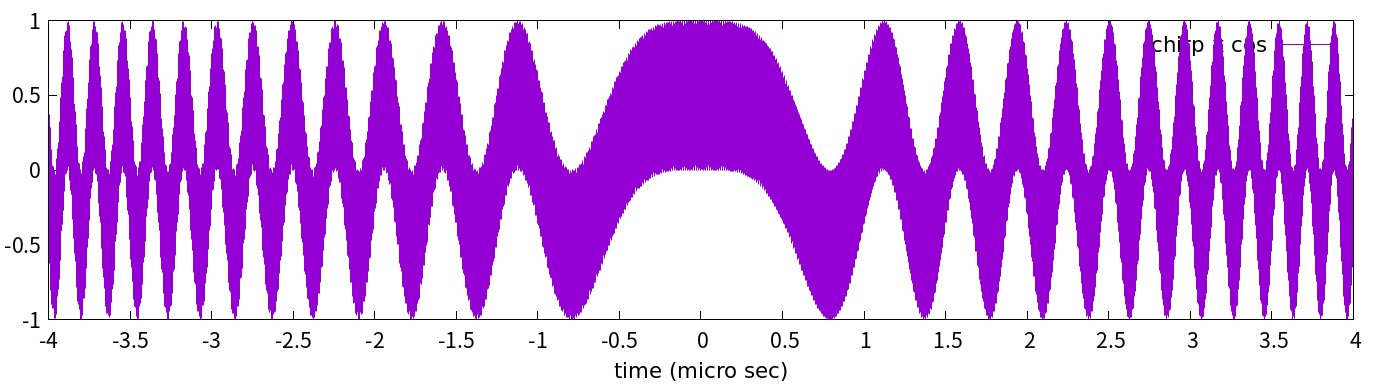
図3-2
何やら思わせぶりな形ですね。べったり帯状になっているのは, 激しい振動のために潰れているからです。この激しい振動は, 概ね中心周波数の2倍の周波数で構成されています（後で導出します）。そこで, それを高周波カットフィルター（低周波通過フィルター）で除去するのです。といっても原理は簡単で, カットしたい周波数の倍の周波数で移動平均すればよろしい（そうすると, 当該周波数の振動は山と谷が打ち消しあって消えます）。つまり, (1/(2x中心周波数))/2の時間間隔で2点の移動平均をするのです。するとこうなります:
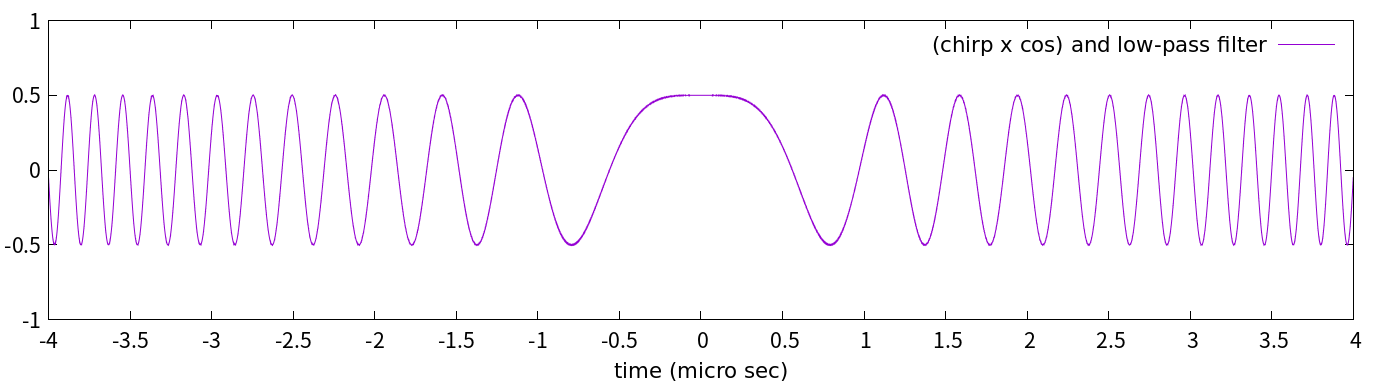
図3-3
これがSARの「生データ」です（先程, 「私の知ってるチャープパルスとは違う!!」と思った人は, これを見て安心したでしょう!!）。
さてこの計算を, 式(2)のようなcosの搬送波だけでなく, sinの搬送波でもやってみましょう。なぜ? cosだけやってsinをやらないのは気持ち悪いじゃないですか（笑）。つまり式(1)に
\sin(2\pi f t)\tag{3-3}\\
を「掛け算」するのです。すると次のようになります:
\cos(2\pi f t + \alpha t^2)\sin(2\pi f t)\tag{3-4}\\
グラフにしてみましょう。まず単に掛け算しただけ(式(3-4))のがこちら:
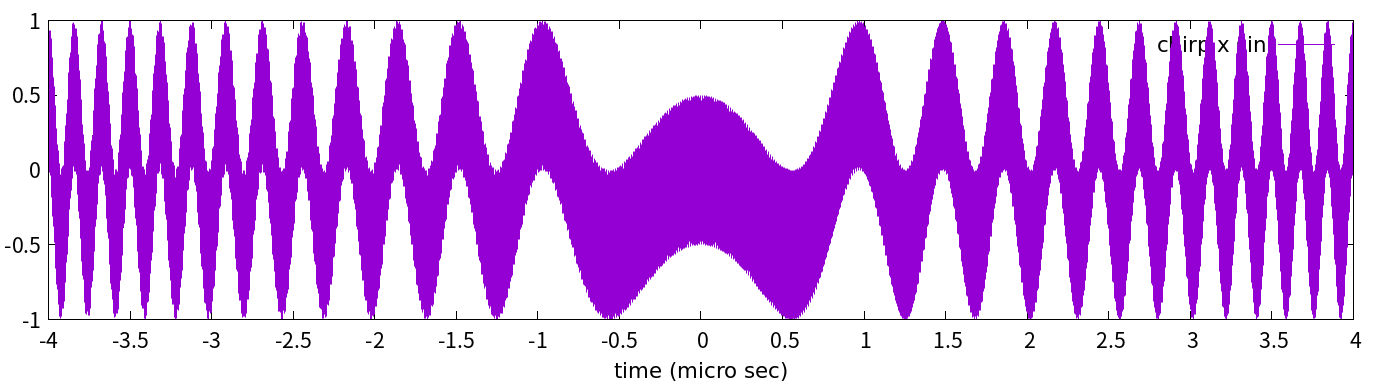
図3-4
そしてそれを低周波通過フィルタにかけたのがこちらです:
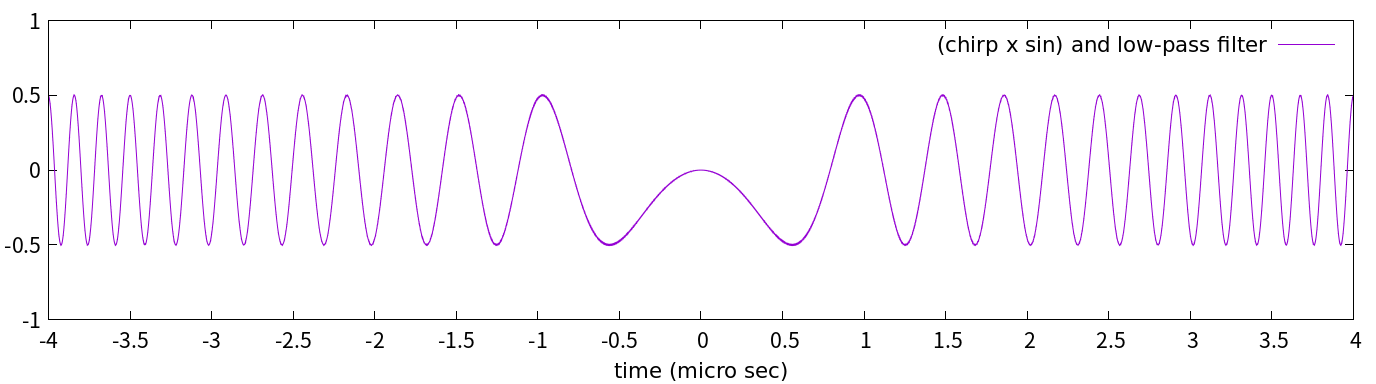
図3-5
4. 複素数出現!!
ここまでで見たような, cosとsinのそれぞれの搬送波を掛けてフィルターをかけた2つの信号を重ねてプロットしたらこうなります:
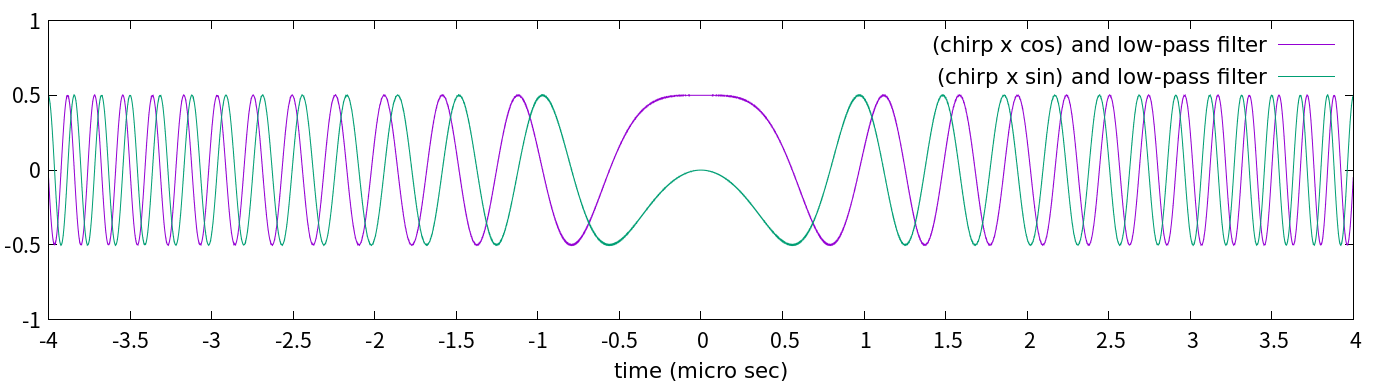
図4-1
この2つの線は, ともに１つのチャープパルス(式(1))から作られたことに注意して下さい。この2つをそれぞれ実部と虚部とみなすことで, 複素数になるのです。
5. 変調と復調
ところで式(1-1)で$f=0$とした関数を考えましょう:
\cos(\alpha t^2)\tag{5-1}
これはいわば「中心周波数0のチャープパルス」です。これのsin版も考えましょう（便宜上, マイナスをつけておきます）:
-\sin(\alpha t^2)\tag{5-2}
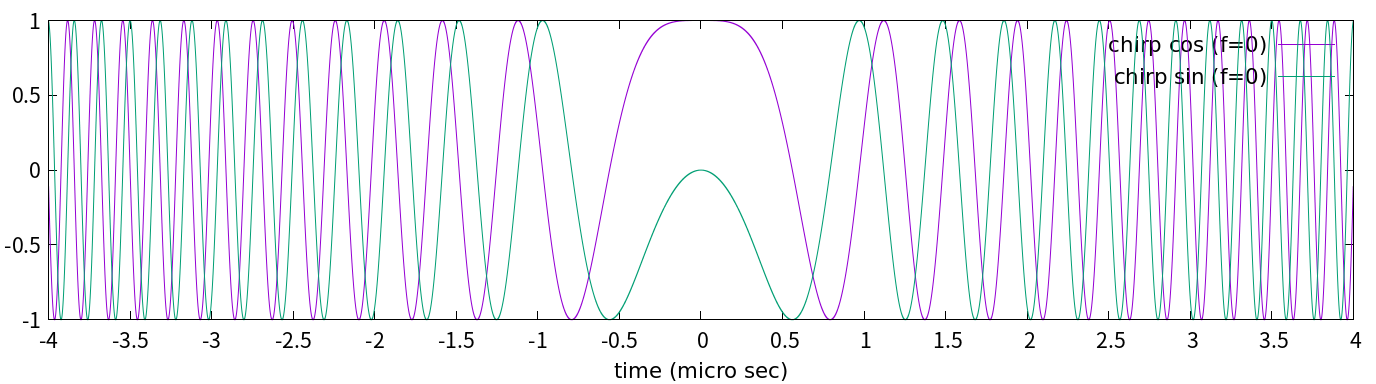
これらを重ねてグラフに描くとこうなります:
図5-1
これを図4-1と比べてみて下さい。振幅は違うけど, 形は全く同じではないですか!!実は, 図4-1は, 図5-1を「変調」し, 「復調」したものなのです。変調とは信号の周波数を変えることで, 復調とはそれを元の周波数に戻すことです。なぜ周波数を変えるのか? それは最初に述べたように, 宇宙から地表を覗ける電波には, 周波数の制約があるからです（他にも理由はありますが割愛）。図5-1の元になった式(5-1)に, 中心周波数$f$の振動を入れ込んで式(1-1)のようにしたのです。これが変調です。変調された電波は衛星と地表の間でキャッチボールされ, 無事に衛星に戻ってきます。それを式(3-2)のように搬送波と掛けてローパスフィルターを通すと元の信号に戻ります。それが復調です。
式(1-1)はcosの中に$ft$という項が付け加わっています。これによって, cosの表す振動の周波数が$f$だけ上がり（中心周波数）, それをもとの$\alpha t$の項で変化させていると見ることができます。このように, 周波数を変化させることで信号を変調するやりかたを周波数変調（frequency modulation; FM）といいます。
ここでひとつ疑問が生じます。式(1-1)はコサインのチャープパルス（式(5-1))を変調したものなのに, それを復調するとコサインのチャープパルス（図4-1の紫線）だけでなくサインのチャープパルス（式(5-2)）が出てくる（図4-1の緑線）ではないですか!なぜでしょう!? 私はずっとこれが不思議でした。でも答えは簡単でした。式(1-1)を加法定理で分解してみましょう:
\cos(2\pi f t + \alpha t^2)=\cos(2\pi f t)\cos(\alpha t^2)-\sin(2\pi f t)\sin(\alpha t^2)
\tag{5-3}
なんと, コサインのチャープパルス（$\cos(\alpha t^2)$）とサインのチャープパルス（$\sin(\alpha t^2)$）の両方が入っているではないですか!!つまり, 式(1-1)（それは式(5-3)の左辺と同じ)で$f=0$とすればコサインのチャープパルスだけだけど, 実際は$f$は0でないし, それどころか大変大きな値（1300 MHz; それにくらべて$\alpha t$は40 MHzくらい）をとるのであり, その$ft$のおかげで, 変調されたチャープパルスの中にはサインのチャープパルスもちゃんと入っているのです。つまり, 式(1-1)は, 「コサインのチャープパルスとサインのチャープパルスの両方を含んで変調されたチャープパルス」なのです。
6. 距離と位相
これまでターゲットへの距離が0だとして考えてきました。実際はそんなことありません（笑）。衛星と地表の距離は700 kmくらいあります。
ここではまずそこまで離さないで, わずかな距離$\Delta x$だけ離れた場合を考えましょう。すると, 衛星に電波が戻ってくるのに, $2\Delta x/c$だけタイムラグが生じます（$c$は光速）。この2は往復で距離が倍になることを意味します。つまり, 時刻$t$に受信する信号は, 時刻$t-2\Delta x/c$に送信された信号です。というわけで,
\cos(2\pi f(t-2\Delta x/c)+\alpha (t-2\Delta x/c)^2)\tag{6-3}
が受信信号になります。これを復調（cosとsinの搬送波を掛けてローパスフィルタに通す）してみましょう。その一例がこちらです:
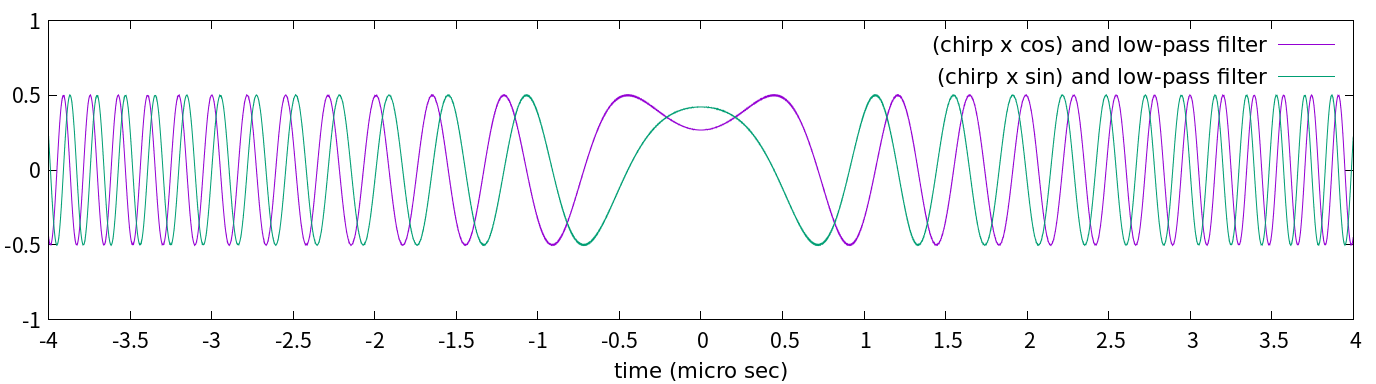
図6-1
これはターゲットとの距離が「搬送波の波長の0.08倍」のとき, つまり約1.9 cmの場合の計算結果です。これを図4-1（ターゲットとの距離が0の場合）と比べてみましょう。時刻0（グラフの真ん中）で, 紫のピークが凹んで, 緑のピークが上がっていますね。この紫と緑はそれぞれcosとsinの搬送波で復調したものですが, それらの形はもはやcosのチャープパルスにもsinのチャープパルスにも一致しません。実は, これらはそれぞれがcosのチャープパルスとsinのチャープパルスの「重ね合わせ」になっているのです。そしてこのグラフから明らかなように, このわずか1.9 cmの距離の差で, 復調された受信信号の形は（図4-1から）大きく変化するのです。この特徴を, cosとsinのそれぞれの復調信号を実部と虚部にした複素数で考えてその偏角（実軸からの角で表した位相）で表現するのですが, マイクロ波の反射の強さの分布だけに興味がある場合は, そのような特徴は捨てられてしまいます。それを捨てずに利用するのが干渉SARやコヒーレンスという解析手法です。
次に, 距離をだいぶ離してみましょう。といっても700 kmまではまだまだですが, とりあえず150 m離してみます:
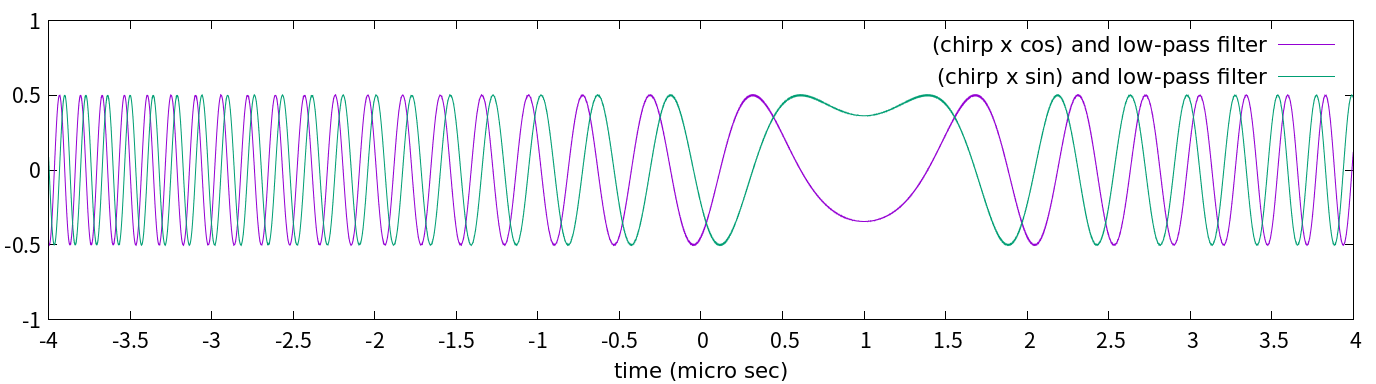
図6-2
図4-1と比べると, グラフの形が変わっている以外に, 全体的に右にシフトしています。中心がだいたい1 μsくらいずれていますね。この時間に光速（$3.0\times10^8$ m/s）をかけてみると, 300 mになります。つまり150 mを往復する距離です。さきほど「150 m離した」と書きましたが, それと整合する結果です。
これらの2つのグラフを, コサインとサインのチャープパルスのシフトと重ね合わせでぴったり再現できる位置をみつけることで, 実際の距離を正確に計測できるのです。それをレンジ圧縮といいます。
7. sinのチャープパルスはどこに隠れていた?
とりあえずここまででおしまいなのですが, sinのチャープパルスが隠れていたことの説明がいまいち納得できないという人のために, 別の説明を考えてみました。
先に述べたように, sinとcosは平行移動の関係にあります。すなわち, $\cos (x-\pi/2)=\sin x$です。あるいは, $\cos (x+\pi/2)=-\sin x$です。つまり, cosの中をプラスかマイナスのいずれかに$\pi/2$だけズラせば（符号はともあれ）sinが出てきます。それを念頭に, 式(1-1)を見てみましょう:
\cos(2\pi f t + \alpha t^2)\tag{1-1}
この$t$をわずかに$\Delta t$だけズラしてみましょう:
\begin{align}
\cos(2\pi f (t+\Delta t) + \alpha (t+\Delta t)^2)\\
= \cos(2\pi ft + 2\pi f\Delta t + \alpha t^2 + 2\alpha t \Delta t + \alpha \Delta t^2)\\
= \cos(2\pi ft + \alpha t^2 + 2(\pi f+\alpha t) \Delta t + \alpha \Delta t^2)
\tag{7-1}
\end{align}
ここで, 式(7-1)のcosの中の第3項が, $2(\pi f + \alpha t)\Delta t = \pi/2$となるように$\Delta t$をとりましょう。つまり,
\Delta t = \frac{1}{4( f + \alpha t/\pi)}\tag{7-2}
とするのです。すると, 式(7-1)はこうなってsinが出てきます!!:
\cos(2\pi ft + \alpha t^2 + \pi/2+\alpha\Delta t^2)=-\sin(2\pi ft + \alpha t^2 + \alpha\Delta t^2)\tag{7-3}
ここで$\alpha\Delta t^2$が邪魔ですが, こいつは大変小さい（0に近い）ことを確認しましょう: PALSAR-2では$\alpha$は5 MHz/μs, $f$は1300 MHz程度, $|t|<20$ μsですから,
\begin{align}
\Delta t =\frac{1}{4(f + \alpha t/\pi)} < \frac{1}{4(1300\text{ MHz} - 5(\text{ MHz/μs}) \times 20\text{μs}/\pi)}\\
\fallingdotseq 2.0\times 10^{-4}\text{μs}\tag{7-4}
\end{align}
従って,
\alpha\Delta t^2 < 5 \text{MHz/μs} \times (2.0\times 10^{-4}\text{μs})^2 < 2.0\times 10^{-7}\text{ラジアン}\tag{7-5}
というわけで, $\alpha\Delta t^2$は三角関数の値をほぼ変えないため, 実質的に無視できます。すると式(7-3)はこうなります:
-\sin(2\pi ft + \alpha t^2)\tag{7-5}
つまり, 変調されたsinのチャープパルス（式(1.1)のcosをsinにしたもの）が, 隠れていたことがわかります。どこに隠れていたかと言うと, 変調されたcosのチャープパルスのすぐそば（$\Delta t$だけズレたところ）です。
変調前のチャープパルスは, 時間的にゆっくり変動するシグナルです。それを変調すると, 途端にせわしなく変動するシグナルになります。といっても, そのせわしない変動成分$ft$は位相を高速で回転させるだけです。その回転が, あるタイミングでcosの位相(0)になり, その直後にsinの位相($\pi/2$)になる, ということをめまぐるしく繰り返すので, 結果的に, cosとsinの両方のチャープパルスをめまぐるしく入れ替えながら表現しているということです。