#やりたいこと
- アンサンブル学習におけるバギングを用いた決定株分類器から決定木分類器を実装する
※アンサンブル学習・・・性能の低い学習器を組み合わせて高性能な学習器を作るという枠組み
#環境
- OS X El Capitan
- Python 3.4.3-0
- Anaconda - spyder:Version 2.3.5.2
#参考
イラストで学ぶ機械学習 小二乗法による識別モデル学習を中心に (KS情報科学専門書)
アンサンブル学習の章にあるバギング
https://www.amazon.co.jp/dp/4061538217
#決定株分類器
あるデータの入力変数どれか一つを選び、その値によって閾値を設定し分類をするというもの
何次元のデータであろうともそこから1次元選び、ソートして最もクラスを分類できる値を決めるだけなのでとっても単純である
実際にコードを書いてみる
#分類するデータ
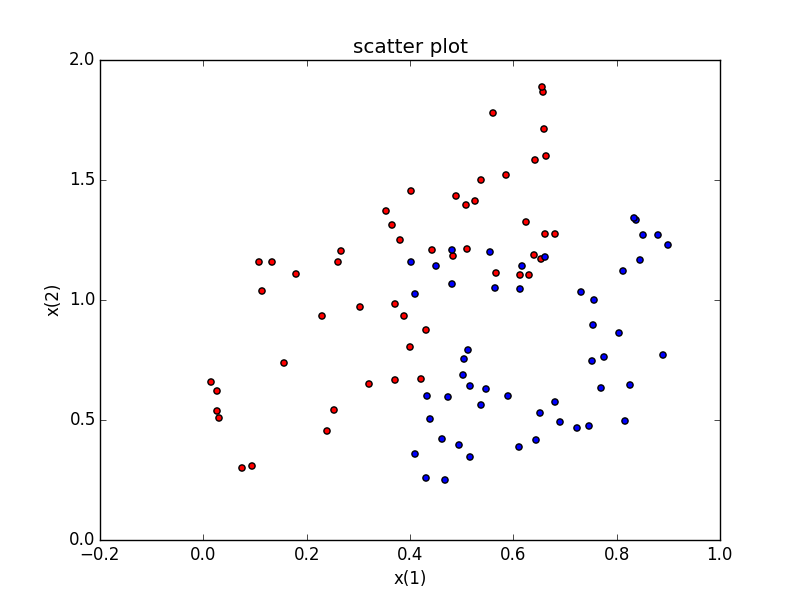
今回分類するデータはこちら
決定株では完全には分類しきれないものにしました
from matplotlib import pyplot as plt
import numpy as np
#散布図を用意
x1 = np.random.rand(50)*0.7
y1 = 1.5*x1+np.random.rand(50)
z1 = np.array([1]*50)
data1 = np.array([x1,y1,z1]).T #.Tは転置
x2 = np.random.rand(50)*0.5 + 0.4
y2 = 0.5*x2+np.random.rand(50)
z2 = [-1]*50
data2 = np.array([x2,y2,z2]).T #.Tは転置
fig = plt.figure()
ax = fig.add_subplot(1,1,1)#重ねてプロットできるようにしている
ax.scatter(data1[:,0],data1[:,1], c='red')
ax.scatter(data2[:,0],data2[:,1], c='blue')
ax.set_title('scatter plot')
ax.set_xlabel('x(1)')
ax.set_ylabel('x(2)')
fig.show()
###赤データ(data1)
データ数50
x(1) x(2) class
array([[ 0.65835714, 1.86611433, 1. ],
[ 0.3534892 , 1.37090828, 1. ],
[ 0.26053953, 1.15649857, 1. ],
[ 0.58657458, 1.5199289 , 1. ],
[ 0.02606646, 0.5383575 , 1. ],
[ 0.25357011, 0.53960271, 1. ],
[ 0.10860395, 1.1602237 , 1. ],
[ 0.67993037, 1.27370855, 1. ],
[ 0.09453285, 0.30877097, 1. ],
[ 0.364833 , 1.31188238, 1. ],
[ 0.13220111, 1.15644224, 1. ],
[ 0.44197415, 1.20773594, 1. ],
[ 0.32057424, 0.64984045, 1. ],
[ 0.26661592, 1.20548853, 1. ],
[ 0.48920851, 1.43340794, 1. ],
[ 0.37102687, 0.98295108, 1. ],
[ 0.37008336, 0.6678845 , 1. ],
[ 0.63035162, 1.10450775, 1. ],
[ 0.66248159, 1.59943389, 1. ],
[ 0.53676978, 1.50064507, 1. ],
[ 0.23044885, 0.9317878 , 1. ],
[ 0.62504023, 1.32471047, 1. ],
[ 0.56043846, 1.77900221, 1. ],
[ 0.38841462, 0.93539729, 1. ],
[ 0.39953475, 0.8051385 , 1. ],
[ 0.65902101, 1.71171347, 1. ],
[ 0.65324475, 1.16881475, 1. ],
[ 0.24014986, 0.45252189, 1. ],
[ 0.03000273, 0.50767001, 1. ],
[ 0.17902989, 1.10688828, 1. ],
[ 0.11412494, 1.03705778, 1. ],
[ 0.40100179, 1.45337063, 1. ],
[ 0.52587804, 1.41153833, 1. ],
[ 0.65513374, 1.8872856 , 1. ],
[ 0.30233462, 0.96967813, 1. ],
[ 0.61344714, 1.10598154, 1. ],
[ 0.51111853, 1.21090783, 1. ],
[ 0.02649236, 0.6227115 , 1. ],
[ 0.43167003, 0.87498462, 1. ],
[ 0.66111293, 1.27690263, 1. ],
[ 0.6425841 , 1.58495541, 1. ],
[ 0.56699657, 1.11329601, 1. ],
[ 0.63914643, 1.1875824 , 1. ],
[ 0.15619608, 0.73724056, 1. ],
[ 0.42081009, 0.67172216, 1. ],
[ 0.48237784, 1.18324757, 1. ],
[ 0.01462027, 0.6564728 , 1. ],
[ 0.50839416, 1.39391787, 1. ],
[ 0.0739257 , 0.29977146, 1. ],
[ 0.38142819, 1.25095399, 1. ]])
###青データ(data2)
データ数50
x(1) x(2) class
array([[ 0.45029784, 1.14289213, -1. ],
[ 0.40972526, 0.35874932, -1. ],
[ 0.43359833, 0.60175114, -1. ],
[ 0.50175972, 0.68781192, -1. ],
[ 0.65234794, 0.53031726, -1. ],
[ 0.40176075, 1.16036674, -1. ],
[ 0.51544749, 0.34465409, -1. ],
[ 0.72273398, 0.46638663, -1. ],
[ 0.81571797, 0.49500299, -1. ],
[ 0.74584354, 0.47481248, -1. ],
[ 0.80463224, 0.86273535, -1. ],
[ 0.8379017 , 1.33387869, -1. ],
[ 0.46699886, 0.24904109, -1. ],
[ 0.89991606, 1.227647 , -1. ],
[ 0.56539962, 1.05127334, -1. ],
[ 0.82490304, 0.64523456, -1. ],
[ 0.58891351, 0.59973919, -1. ],
[ 0.64420597, 0.41463488, -1. ],
[ 0.53813948, 0.56380257, -1. ],
[ 0.7689858 , 0.63429867, -1. ],
[ 0.51217495, 0.79023256, -1. ],
[ 0.68981807, 0.49096141, -1. ],
[ 0.61761692, 1.14192141, -1. ],
[ 0.54758393, 0.62849744, -1. ],
[ 0.77453459, 0.76392961, -1. ],
[ 0.55454527, 1.20157888, -1. ],
[ 0.68131782, 0.57450653, -1. ],
[ 0.49443341, 0.3958763 , -1. ],
[ 0.43889704, 0.50518871, -1. ],
[ 0.51678849, 0.64334286, -1. ],
[ 0.46159915, 0.42016756, -1. ],
[ 0.61281401, 1.04538677, -1. ],
[ 0.40984895, 1.02317007, -1. ],
[ 0.8902936 , 0.76918085, -1. ],
[ 0.83378338, 1.34146463, -1. ],
[ 0.75325306, 0.89706332, -1. ],
[ 0.75142634, 0.74712067, -1. ],
[ 0.50358951, 0.75265145, -1. ],
[ 0.87987733, 1.26875816, -1. ],
[ 0.48114754, 1.06587256, -1. ],
[ 0.81215201, 1.12255637, -1. ],
[ 0.6104651 , 0.389084 , -1. ],
[ 0.66137085, 1.17964222, -1. ],
[ 0.7556205 , 1.00065754, -1. ],
[ 0.48128905, 1.21040627, -1. ],
[ 0.43181014, 0.25963079, -1. ],
[ 0.84516368, 1.16532771, -1. ],
[ 0.73130899, 1.0314929 , -1. ],
[ 0.4738698 , 0.59377616, -1. ],
[ 0.85049286, 1.27035715, -1. ]])
#境界線を決める
x(1)を基準として境界線を引こうと思うので、まずdata1,data2を結合しx(1)基準でソートする
#赤、青両方のデータを結合してx(1)の値でソートする
bindData = np.r_[data1,data2][:,0].argsort() #昇順にソートしたインデックス取得
sortedData = np.r_[bindData]
するとデータはこのようになる
x(1) x(2) class
array([[ 0.01462027, 0.6564728 , 1. ],
[ 0.02606646, 0.5383575 , 1. ],
[ 0.02649236, 0.6227115 , 1. ],
[ 0.03000273, 0.50767001, 1. ],
[ 0.0739257 , 0.29977146, 1. ],
[ 0.09453285, 0.30877097, 1. ],
[ 0.10860395, 1.1602237 , 1. ],
[ 0.11412494, 1.03705778, 1. ],
[ 0.13220111, 1.15644224, 1. ],
[ 0.15619608, 0.73724056, 1. ],
[ 0.17902989, 1.10688828, 1. ],
[ 0.23044885, 0.9317878 , 1. ],
[ 0.24014986, 0.45252189, 1. ],
[ 0.25357011, 0.53960271, 1. ],
[ 0.26053953, 1.15649857, 1. ],
[ 0.26661592, 1.20548853, 1. ],
[ 0.30233462, 0.96967813, 1. ],
[ 0.32057424, 0.64984045, 1. ],
[ 0.3534892 , 1.37090828, 1. ],
[ 0.364833 , 1.31188238, 1. ],
[ 0.37008336, 0.6678845 , 1. ],
[ 0.37102687, 0.98295108, 1. ],
[ 0.38142819, 1.25095399, 1. ],
[ 0.38841462, 0.93539729, 1. ],
[ 0.39953475, 0.8051385 , 1. ],
[ 0.40100179, 1.45337063, 1. ],
[ 0.40176075, 1.16036674, -1. ],
[ 0.40972526, 0.35874932, -1. ],
[ 0.40984895, 1.02317007, -1. ],
[ 0.42081009, 0.67172216, 1. ],
[ 0.43167003, 0.87498462, 1. ],
[ 0.43181014, 0.25963079, -1. ],
[ 0.43359833, 0.60175114, -1. ],
[ 0.43889704, 0.50518871, -1. ],
[ 0.44197415, 1.20773594, 1. ],
[ 0.45029784, 1.14289213, -1. ],
[ 0.46159915, 0.42016756, -1. ],
[ 0.46699886, 0.24904109, -1. ],
[ 0.4738698 , 0.59377616, -1. ],
[ 0.48114754, 1.06587256, -1. ],
[ 0.48128905, 1.21040627, -1. ],
[ 0.48237784, 1.18324757, 1. ],
[ 0.48920851, 1.43340794, 1. ],
[ 0.49443341, 0.3958763 , -1. ],
[ 0.50175972, 0.68781192, -1. ],
[ 0.50358951, 0.75265145, -1. ],
[ 0.50839416, 1.39391787, 1. ],
[ 0.51111853, 1.21090783, 1. ],
[ 0.51217495, 0.79023256, -1. ],
[ 0.51544749, 0.34465409, -1. ],
[ 0.51678849, 0.64334286, -1. ],
[ 0.52587804, 1.41153833, 1. ],
[ 0.53676978, 1.50064507, 1. ],
[ 0.53813948, 0.56380257, -1. ],
[ 0.54758393, 0.62849744, -1. ],
[ 0.55454527, 1.20157888, -1. ],
[ 0.56043846, 1.77900221, 1. ],
[ 0.56539962, 1.05127334, -1. ],
[ 0.56699657, 1.11329601, 1. ],
[ 0.58657458, 1.5199289 , 1. ],
[ 0.58891351, 0.59973919, -1. ],
[ 0.6104651 , 0.389084 , -1. ],
[ 0.61281401, 1.04538677, -1. ],
[ 0.61344714, 1.10598154, 1. ],
[ 0.61761692, 1.14192141, -1. ],
[ 0.62504023, 1.32471047, 1. ],
[ 0.63035162, 1.10450775, 1. ],
[ 0.63914643, 1.1875824 , 1. ],
[ 0.6425841 , 1.58495541, 1. ],
[ 0.64420597, 0.41463488, -1. ],
[ 0.65234794, 0.53031726, -1. ],
[ 0.65324475, 1.16881475, 1. ],
[ 0.65513374, 1.8872856 , 1. ],
[ 0.65835714, 1.86611433, 1. ],
[ 0.65902101, 1.71171347, 1. ],
[ 0.66111293, 1.27690263, 1. ],
[ 0.66137085, 1.17964222, -1. ],
[ 0.66248159, 1.59943389, 1. ],
[ 0.67993037, 1.27370855, 1. ],
[ 0.68131782, 0.57450653, -1. ],
[ 0.68981807, 0.49096141, -1. ],
[ 0.72273398, 0.46638663, -1. ],
[ 0.73130899, 1.0314929 , -1. ],
[ 0.74584354, 0.47481248, -1. ],
[ 0.75142634, 0.74712067, -1. ],
[ 0.75325306, 0.89706332, -1. ],
[ 0.7556205 , 1.00065754, -1. ],
[ 0.7689858 , 0.63429867, -1. ],
[ 0.77453459, 0.76392961, -1. ],
[ 0.80463224, 0.86273535, -1. ],
[ 0.81215201, 1.12255637, -1. ],
[ 0.81571797, 0.49500299, -1. ],
[ 0.82490304, 0.64523456, -1. ],
[ 0.83378338, 1.34146463, -1. ],
[ 0.8379017 , 1.33387869, -1. ],
[ 0.84516368, 1.16532771, -1. ],
[ 0.85049286, 1.27035715, -1. ],
[ 0.87987733, 1.26875816, -1. ],
[ 0.8902936 , 0.76918085, -1. ],
[ 0.89991606, 1.227647 , -1. ]])
初めの方はクラス1(赤色データ)が多いが徐々にクラス−1(青色データ)が多くなっている
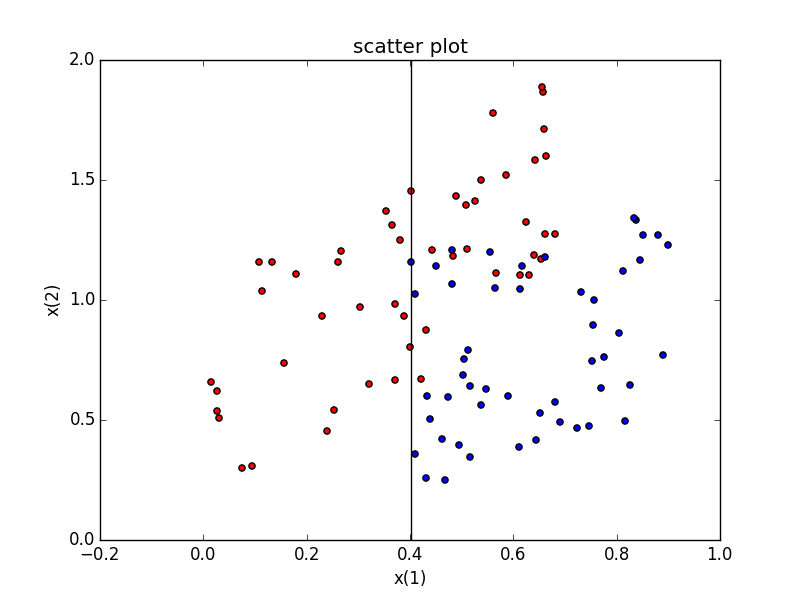
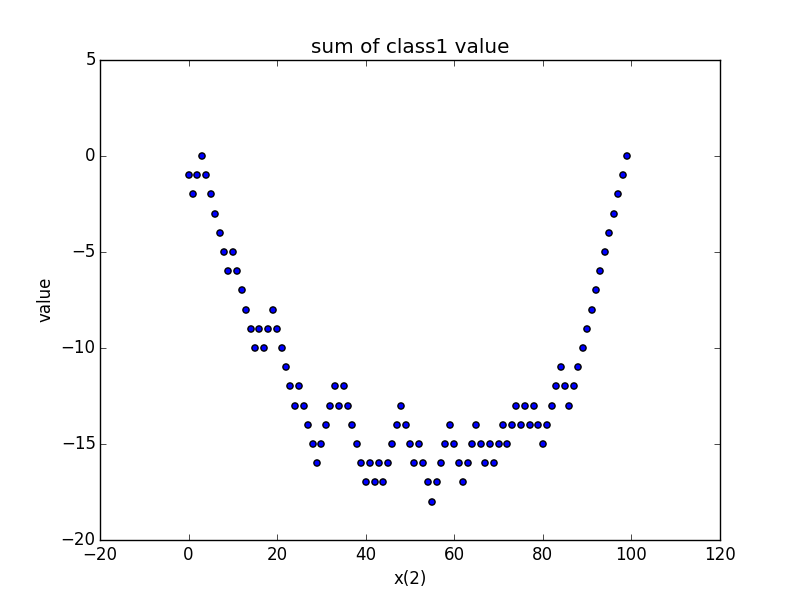
###分離誤差が最小になるx(1)の値を決める
クラスの値を1と−1にしておいたので何個目までをクラス1と判断すればクラス内のクラス値の絶対値の合計が最大化されるかを見れば分離誤差が最小となるx(1)の値がわかる
zValue = 0
max = [0,0]
fig2 = plt.figure()
ax2 = fig2.add_subplot(1,1,1)
ax2.set_title('sum of class1 value')
ax2.set_xlabel('x(1)')
ax2.set_ylabel('value')
for i in range(100):
zValue = zValue + sortedData[i,2]
if fabs(zValue) > fabs(max[1]):
max = [i,zValue]
ax2.scatter(i,zValue)
ax.axvline(x=sortedData[max[0],0],color="black")
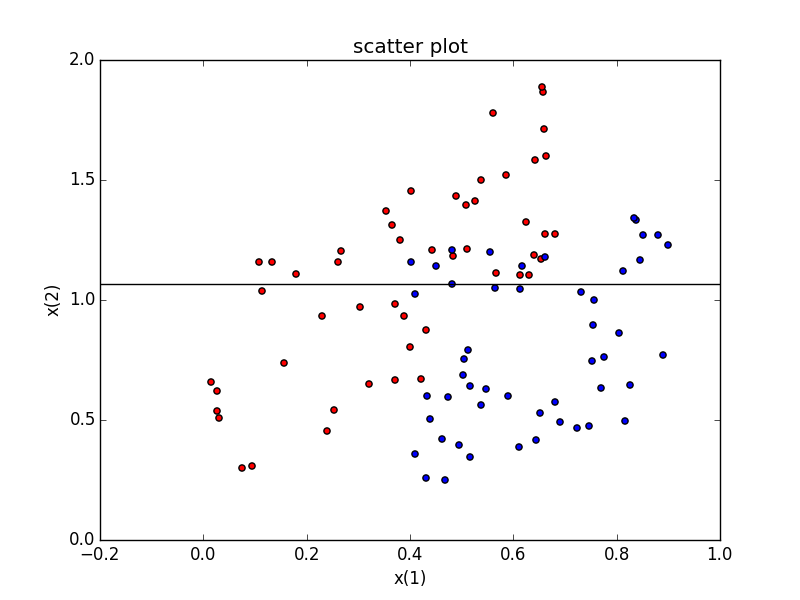
###x(2)でも分類してみる
x(1)でソートしていた部分をx(2)にするだけでできるのでコードは割愛
#バギングを用いて学習する
###バギング・・・?
- バギング:ブートストラップ・アグリゲーションからの造語
- ブートストラップ:N個の訓練標本から重複を許してランダムにN個選ぶ事
- アグリゲーション:集めること
-->バギングとはブートストラップにより擬似的に訓練標本を作成し、何度も何度も学習をして得た学習器の平均を最終的なアウトプットとするアルゴリズム
##学習器をx(1),x(2)についてそれぞれ2000ずつ用意し、識別境界を求める
上で行ってきた弱学習器による、境界線算出をブートストラップによって得られたデータで2000回行う(x(1)*1000回、x(2)*1000回とした)
次に、グラフ上の各座標における2000個の学習器による識別結果の平均を算出し、その境界線となるところに線を引いた
完全には識別しきれていないが、まぁ学習はしていることが見受けられた
誤識別されたのは100個中5個!
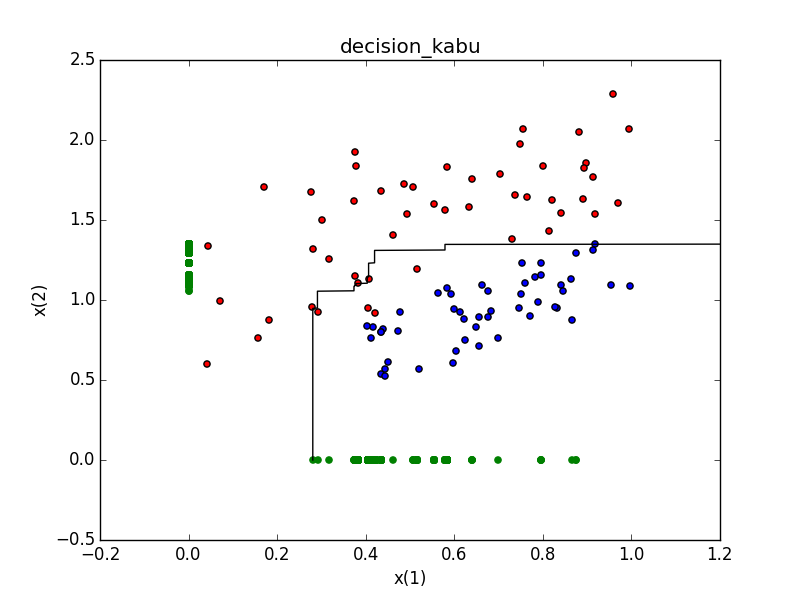
※緑の点は2000ある識別境界の位置(本当は直線)
※ここのデータが変わってしまっているのは、完全に上のデータが少しクラス同士混じりすぎていたので、単純にするため
# -*- coding: utf-8 -*-
import random
import math
from matplotlib import pyplot as plt
import numpy as np
#bootstrap
#引数:一次元のリスト
#返り値:一次元のリスト
def bootstrap(dataArray):
arrayColumn = len(dataArray)
outArray = np.zeros((arrayColumn,len(dataArray[0])))
for i in range(arrayColumn):
outArray[i] = dataArray[random.randint(0,arrayColumn - 1)]
return outArray
#境界線を求める
#引数:2種類のデータ
#返り値:X、Yの境界線の値
def learnBorder(data1,data2):
Xmax = 0
Ymax = 0
for k in [0,1]:
# 昇順ソート
bindData = np.r_[data1,data2][:,k].argsort()
sortedData = np.r_[data1,data2][bindData]
zValue = 0
max = [0,0]
for i in range(len(sortedData)):
zValue = zValue + sortedData[i,2]
if ( math.fabs(zValue) > math.fabs(max[1])):
max = [i,zValue]
if k == 0:
Xmax = sortedData[max[0],k]
else:
Ymax = sortedData[max[0],k]
return [Xmax,Ymax]
#複数回学習し、結果の境界線の座標リストを返す
#num:学習回数
def makeBorderList(data1,data2,num):
outArray = np.zeros((num,2))
for i in range(num):
outArray[i] = learnBorder(bootstrap(data1),bootstrap(data2))
return outArray
#学習して得られた境界線をもとにして、最終的な境界線を求める
#引数:X軸、Y軸における境界線のリスト
#返り値:座標リスト
def makeCoordinateData(Xborder,Yborder):
coordinateData = np.array([[0.00]*1000,[0.00]*1000]).T
for m in range(0,1000):
Xresult = [0,10000000]
result_y = 0
for k in range(len(Yborder)):
if m*0.0025 >= Yborder[k]:
result_y = result_y + 1
else:
result_y = result_y + -1
for j in range(0,1000):
result_x = result_y
for i in range(len(Xborder)):
if j*0.0015 <= Xborder[i]:
result_x = result_x + 1
else:
result_x = result_x + -1
if math.fabs(result_x) <= math.fabs(Xresult[1]):
Xresult = [j*0.0015,result_x]
if (j % 1000) == 0:
print(j,m)
coordinateData[m,:] = [j*0.0015,m*0.0025]
return coordinateData
#散布図を用意
x1 = np.random.rand(50)
y1 = 1*x1+np.random.rand(50)*1.1+0.5
z1 = np.array([1]*50)
data1 = np.array([x1,y1,z1]).T #.Tは転置
x2 = np.random.rand(50)*0.6 + 0.4
y2 = 1*x2+np.random.rand(50)*0.5
z2 = [-1]*50
data2 = np.array([x2,y2,z2]).T #.Tは転置
numOfLearn = 2000 #学習回数
L=makeBorderList(data1,data2,numOfLearn)
K = makeCoordinateData(L[:,0],L[:,1])
plt.figure()
plt.hold(True)
plt.title('decision_kabu')
plt.xlabel('x(1)')
plt.ylabel('x(2)')
plt.scatter(data2[:,0],data2[:,1], c='blue')
plt.scatter(data1[:,0],data1[:,1], c='red')
for i in range(1000):#各境界線の位置
plt.scatter(L[i,0],0,color="green")
plt.scatter(0,L[i,1],color="green")
plt.plot(K[:,0],K[:,1],color="black")
#ひとこと
- 仕組みは単純なのに結構強力!
#コード
- 今回使ったコードの一部を載せておきます
https://github.com/kwacgit/decision_stunmp_baging