毎回忘れてしまうのでメモ
前提
隣接行列は節点空間から節点空間への線形写像で,元信号を1-hop先へ写す.

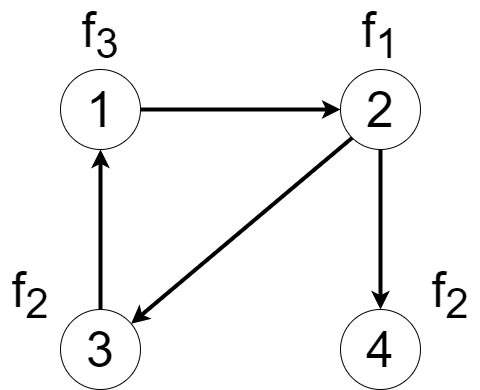
左図の元信号を隣接行列で写すと,右図のようになる.
逆に,そのような行列$\boldsymbol{A}$ が有向グラフの隣接行列である.
これを式で表すと,
\boldsymbol{A}(f_1, f_2, f_3, f_4)^\top = (f_3, f_1, f_2, f_2)^\top
となる.
有向グラフの隣接行列
以上の議論から,今回の例における隣接行列は以下のようになる.
\boldsymbol{A} =
\begin{pmatrix}
0 & 0 & 1 & 0 \\
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 1 & 0 & 0
\end{pmatrix}
列ごとに見ると解釈しやすく,各列は元信号がどこに写るかを表している.
例えば,1列目では(2,1)成分のみ1であり,元信号の$f_1$は節点2に写ることを表している.
実際,信号$\boldsymbol{f}$に作用させると,
\boldsymbol{A}\boldsymbol{f} =
\begin{pmatrix}
0 & 0 & 1 & 0 \\
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 1 & 0 & 0
\end{pmatrix}
\begin{pmatrix}
f_1 \\ f_2 \\ f_3 \\ f_4
\end{pmatrix}
=
\begin{pmatrix}
f_3 \\ f_1 \\ f_2 \\ f_2
\end{pmatrix}
となり,たしかに一致する.