1. 概要
1-1.時系列データとは
改訂版 日本統計学会公式認定 統計検定2級対応 統計学基礎 日本統計学会編 (以下、「教科書」と呼ぶ)の1.7.1節には次のように書いてある。
(前略)時間の順に得られたデータを時系列データ(time series data)という. この時系列データは折れ線グラフで示すとその様子がよくわかる。
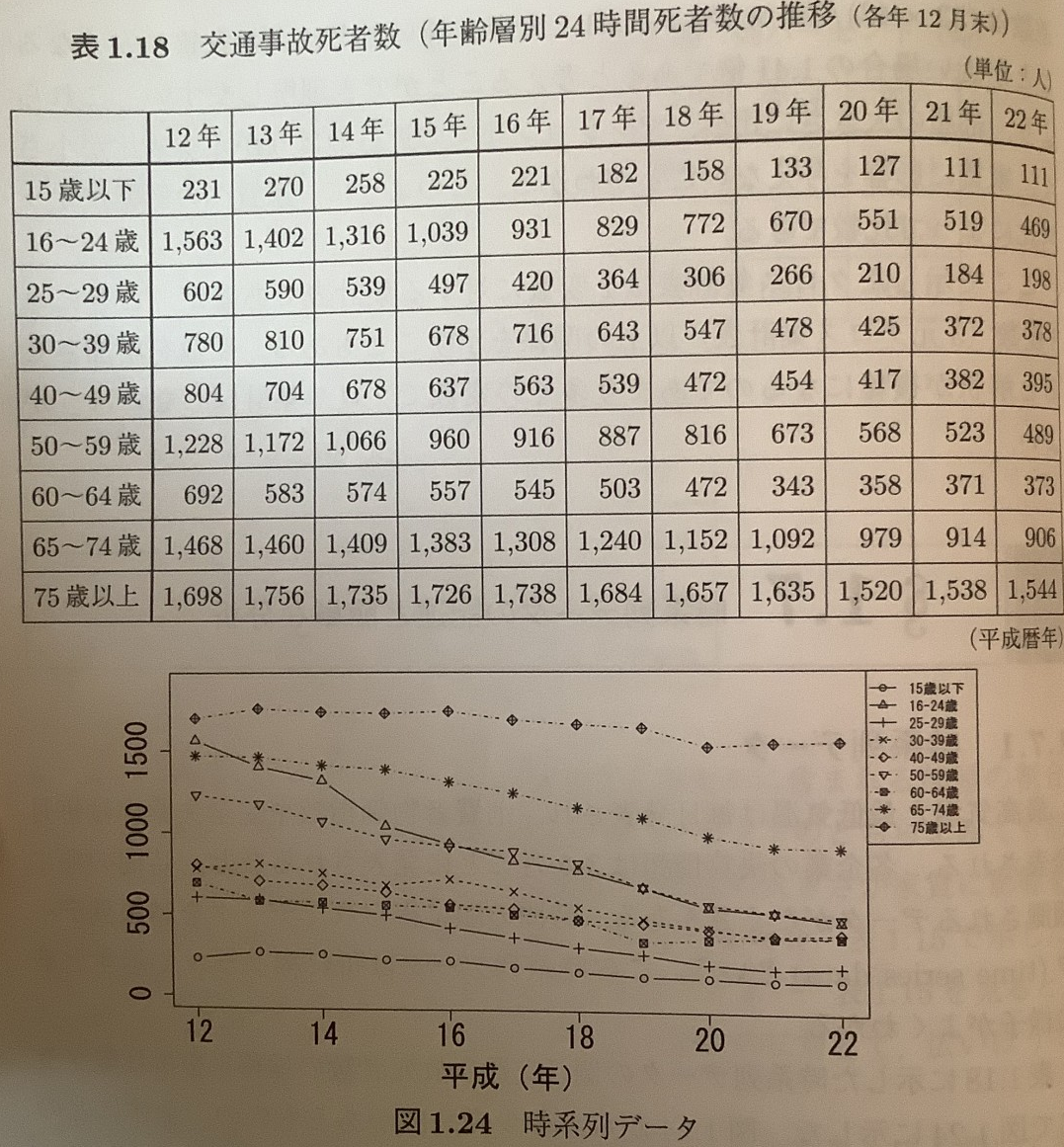
表1.18に示した時系列データの例(交通事故死者数の推移)を折れ線グラフで図1.24に示した. 図1.24から, 多少の凹凸があるものの, 全体にどの年代も死者数が減少していることがわかる. (中略)
時系列データの利用は重要である. 消費者のサービスに関するデータ, たとえば, 窓口に来る客の数を調べることで, 混み合う時間帯や曜日などがわかり, 実際の対応にその結果を活かすことができる. 売れ行きの変動などもその後の企業の戦略などに利用することができる.
1-2. 時系列データの変動分解
教科書によれば、時系列データ$\{y_t\}$の変動は伝統的に次の3要素に分解する考え方があるそうだ。
- 傾向変動$TC_t$ 基本的な長期に渡る動き
- 季節変動$S(1年)_t$ 1年を周期として循環を繰り返す変動
- 不規則変動$I_t$ それら以外
これら3要素の総和がデータに一致するよう分解する。
よって、ここで考えているタスクは次のように説明できる。
$\{TC_t+S(P)_t+I_t\}$を与えるから、そこから$\{TC_t\}$と$\{S(P)_t\}$と$\{I_t\}$を推定せよ。
但し$\{S(P)_t\}$は周期$P$で循環するデータである。
このタスクを行う手順は次の通り。
- $\{TC_t+S(P)_t+I_t\}$の$P$項移動平均により、$\{TC_t\}$を推定する。この推定結果を$\{\hat{TC}_t\}$と書く。
- $\{TC_t-\hat{TC}_t+S(P)_t+I_t\}$の「$t$を$P$で割った余り$m$」毎の平均を求め、これを「細別平均」と呼ぶことにする。
- 「細別平均の平均」を細別平均からそれぞれ引き算することで、$\{\hat{S(P)}_t\}$を求める。$\{\hat{S(P)}_t\}$の平均値は(引き算のおかげで)0となる。
- $\{TC_t-\hat{TC}_t+S(P)_t-\hat{S(P)}_t+I_t\} = \{\hat{I}_t\}$
1-3. 自己相関
教科書1.7.4節より引用
時系列データでは, 周期を扱うので, 同じ時系列の時点をずらした時系列との相関関係が重要となる.
(中略)
時系列データについて, もとの時系列$\{y_t, t=1,2,...,T\}$と時点を$h$だけずらした時系列$\{y_{t+h}, t=1,2,...,T-h\}$を別の変数のデータのように考えて2変数間の相関係数$r_h$を求め, それを$h$の関数とみなしたものを自己相関関数(autocorrelation function)とよぶ.
$h$をラグという。
$r_h$は相関係数の定義式$$r_{xy} := \frac{s_{xy}}{s_xs_y}$$に則って計算してもよいが
$$r_h ≃ \frac{自己共分散(ラグ=h)}{自己共分散(ラグ=0)}$$
と近似計算する方が効率よかったりする。
何で?
ちなみに$$自己共分散(ラグ=h):=\frac{1}{T}\sum^{T-h}_{t=1}{(y_t-\bar{y})(y_{t+h}-\bar{y})}$$である。
また、横軸にラグ、縦軸に$r_h$を示した棒グラフをコレログラムという。コレログラムからは周期性を読み取れる。
次に、教科書に載っていた「東京での月間給与」及びそのコレログラムを引用する。
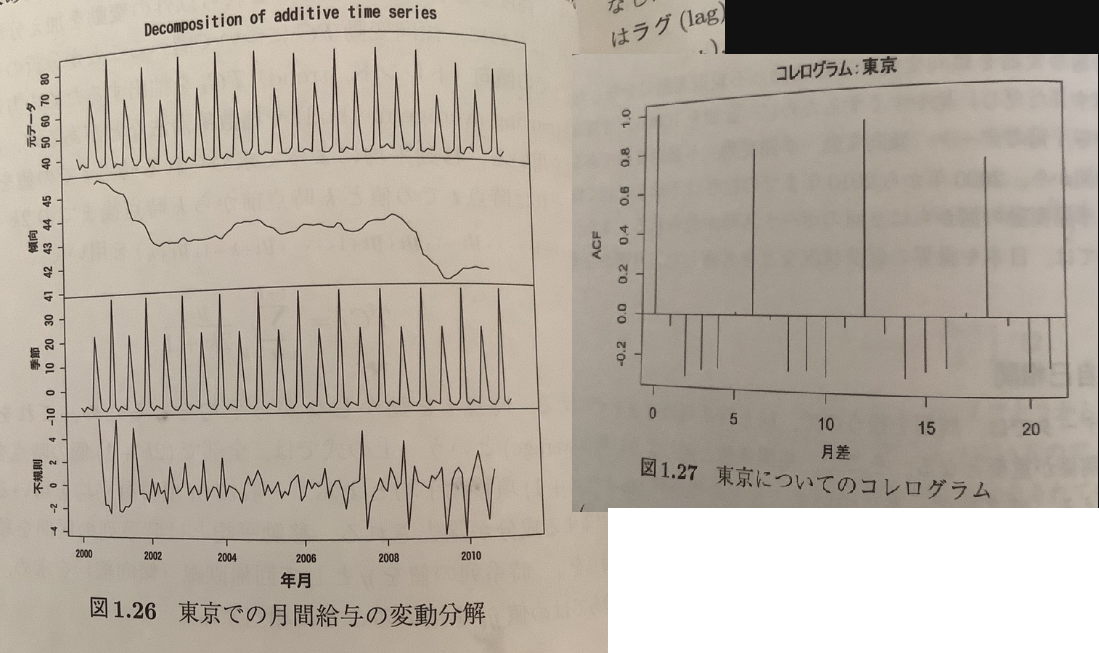
コレログラムを見ると、6か月ごとに高い正の相関が認められる。これは日本企業ではよくある「ボーナス」が影響しているものと考えられる。
2. やりたいこと
変動分析を行うツールと自己相関を計算してコレログラムを作成するツールをpythonで作りたい。
whython?(何でpythonに拘るの?)
- ぶっちゃけ慣れているから
- オブジェクト指向により、読みやすいコードが書ける。特にpython3以降はunicodeにも対応。
- それでいてjavaみたいにpublicだとかvoidだとかの「ノイズ」がほとんどない。この意味でも読みやすいコードが書ける。
- sqlite3が付いてくる
- 自分が勤めている会社のPCにインストールしてOKだった
(以上)
3. コード設計
3-1. 変動データクラス
変動データクラスは次の操作を行えるクラスとします。
初期化(データ:list(float))を傾向と季節と不規則に分解する(季節の周期: int): [list(float), list(float), list(float)]
ざっくり言うと、「実数のリストを入力すると、傾向、季節、不規則変動がそれぞれ出力される」という感じです。
ソースコードはこちら
class 変動データ:
def __init__(self, データ):
self.__データ = データ
def を傾向と季節と不規則に分解する(self, 季節の周期):
def main():
傾向_季節_不規則 = self.__データ
傾向 = 移動平均of(傾向_季節_不規則, 季節の周期)
季節_不規則 = 各要素を引き算(傾向_季節_不規則, 傾向)
細別平均 = 細別平均of(季節_不規則)
季節 = [値-平均of(細別平均) for 値 in 細別平均]
不規則 = 各要素を引き算(季節_不規則, 季節*((len(季節_不規則) // 季節の周期) + 1))
return [傾向, 季節, 不規則]
def 移動平均of(データ, 項数):
項数 = int(項数)
def main():
移動平均 = list()
if 整数(項数).は奇数である():
k = (項数 - 1)//2
両端の重みを半分にする = False
else:
k = 項数 // 2
両端の重みを半分にする = True
for t in range(0, len(データ)):
移動平均を計算するのに必要なtたち = 範囲(t-k, t+k)
tmp = 0
for 必要なt in 移動平均を計算するのに必要なtたち:
if 必要なtがデータからはみ出る(必要なt):
移動平均.append(None)
tmp = 0
break
else:
tmp += データ[必要なt]/2 if 両端の重みを半分にする and 今両端を見ている(必要なt, t, k) else データ[必要なt]
else:
移動平均.append(tmp / 項数)
return 移動平均
def 必要なtがデータからはみ出る(必要なt):
return (必要なt < 0) or (len(データ) <= 必要なt)
def 今両端を見ている(必要なt, t, k):
return 必要なt == t-k or 必要なt == t+k
return main()
def 各要素を引き算(list1, list2):
return [(None if (elem1 is None) or (elem2 is None) else (elem1 - elem2))for (elem1, elem2) in zip(list1, list2)]
def 細別平均of(データ):
細別平均 = [0]*季節の周期
回数of = [0]*季節の周期
for t in range(0, len(データ)):
if データ[t] is not None:
細別平均[t % 季節の周期] += データ[t]
回数of [t % 季節の周期] += 1
for m in range(0, 季節の周期):
細別平均[m] /= 回数of[m]
return 細別平均
def 平均of(データ):
return sum(データ)/len(データ)
class 整数:
def __init__(self, i) :self.i = int(i)
def は奇数である(self):return bool(self.i % 2)
def は偶数である(self):return bool((self.i+1) % 2)
def 範囲(始点, 終点):
return range(始点, 終点+1)
return main()
(以上)
利用例
from 変動データ import 変動データ
変動データ([0,1,2,3,1,2,3,4,2,3,4,5,3,4,5,6]).を傾向と季節と不規則に分解する(季節の周期=4)
[[None, None, 1.625, 1.875, 2.125, 2.375, 2.625, 2.875, 3.125, 3.375, 3.625, 3.875, 4.125, 4.375, None, None], [-1.125, -0.375, 0.375, 1.125], [None, None, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, None, None]]
結果の0番目は「全体的な増加傾向」を的確に表しているし、
結果の1番目は「周期内で単調増加」しているという特徴を的確に表現している。
また、人工的なデータのため、結果の2番目、不規則変動はすべて0。
(以上)
3-2. 自己相関クラス
自己相関クラスは次の操作を行えるクラスとします。
初期化(データ:list(float))__call__(ラグ:int)を求めコレログラムを作る()
ソースコードはこちら
class 自己相関:
def __init__(self, データ):
self.__データ = [float(データム) for データム in データ]
def __call__(self, ラグ):
ラグ = int(ラグ)
if ラグ >= len(self.__データ):
return None
def main():
return 自己共分散(ラグ=ラグ)/自己共分散(ラグ=0)
def 自己共分散(ラグ):
データ = self.__データ
平均 = sum(データ)/len(データ)
rtn = 0
for t in range(0, len(データ) - ラグ):
rtn += (データ[t] - 平均)*(データ[t+ラグ] - 平均)
rtn /= len(データ)
return rtn
return main()
def を求めコレログラムを作る(self):
# 要 `pip install matplotlib`
from matplotlib import pyplot as plt
ラグたち = list(range(0, len(self.__データ)))
自己相関たち = [self(ラグ) for ラグ in ラグたち]
plt.bar(ラグたち, 自己相関たち)
plt.show()
(以上)
利用例
from matplotlib import pyplot as plt
import numpy as np
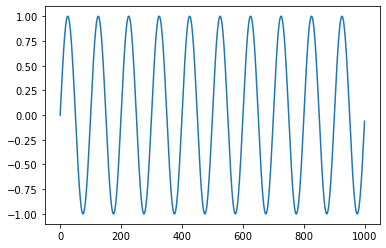
データ = np.sin(2*np.pi*np.arange(1000)/100)
plt.plot(データ)
plt.show()
自己相関(データ).を求めコレログラムを作る()
print("↑振幅1,周期100の正弦波およびそのコレログラム")
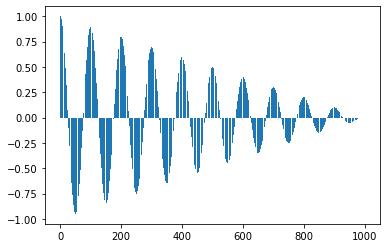
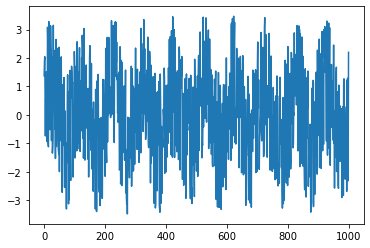
データ2 = np.sin(2*np.pi*np.arange(1000)/100) + (np.random.rand(1000)-0.5)*5
plt.plot(データ2)
plt.show()
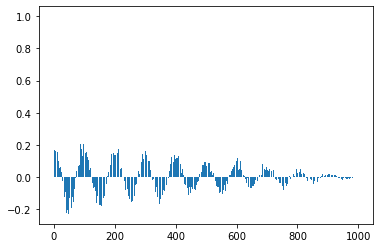
自己相関(データ2).を求めコレログラムを作る()
print("↑振幅1,周期100の正弦波に振幅2.5のノイズを載せた波およびそのコレログラム")
以下、結果。
↑振幅1,周期100の正弦波およびそのコレログラム
↑振幅1,周期100の正弦波に振幅2.5のノイズを載せた波およびそのコレログラム
(以上)
4. 実際のデータ(厚労省のコロナ陽性者数日足データ)を簡単に分析してみる
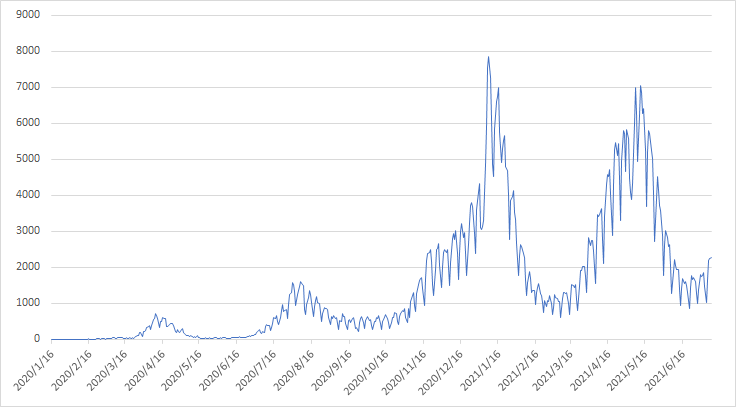
厚生労働省のサイトで公開されている新型コロナ陽性者数のCSVデータは2020/1/16から「一昨日くらい」まで毎日分のデータがある。
グラフにすると次の通り。
4-1. 変動分解
コロナ陽性者数は曜日に強く依存することが知られている。そこで季節周期を7日として変動分解してみよう。
ソースコード
import numpy as np
データ = np.loadtxt("pcr_positive_daily.csv", #ファイルパス
encoding="utf-8", #文字コード。ちゃんと指定しないとUnicodeDecodeErrorが出たりする
delimiter=',', #区切り文字。csvは「Comma Splited Values」なのでcommaを指定。
skiprows=1, #先頭1行読み飛ばす(メタデータ(各列を説明する文字列)なので)
usecols=[1] #1行目が目的の値。0行目は日付データなので要らない
)
[傾向, 季節, 不規則] = 変動データ(データ).を傾向と季節と不規則に分解する(季節の周期=7)
plt.figure(figsize=(32, 8), dpi=500)
plt.plot(range(0, len(データ)), データ)
plt.plot(range(0, len(データ)), 傾向)
plt.plot(range(0, 7), 季節)
plt.plot(range(0, len(データ)), 不規則)
plt.savefig('result.png')
plt.show()
(以上)
こうして得られたresult.pngは次の通り(重くてすみません)。
表. result.pngのグラフの色と意味
| 色 | 意味 |
|---|---|
| 青 | 生データ |
| 橙 | 傾向変動。生データと比べて滑らかになっている |
| 緑 | 季節変動。「曜日変動」と言った方が分かりやすい。 最初1週間分だけ示した。 生データは木曜日から始まっていることに注意 |
| 赤 | 不規則変動。一日8000人近くの陽性が確認されたときにおいても不規則成分は1000人強ほど。 |
さて、yahooニュースの記事では次のことを言っている。
- 「月曜日」の新規感染者が少ない
- 東京都で「木曜日」に感染者数が多い
- 大阪、福岡で「土曜日」に最多を記録した
今回の実験でも「月曜日に少ない」、「木曜日と土曜日に多い」という傾向が読み取れるか。これは緑のグラフに注目するとよい。
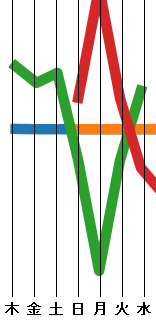
ピタリと一致した。
4-2.コレログラム
ソースコード
import numpy as np
データ = np.loadtxt("pcr_positive_daily.csv", #ファイルパス
encoding="utf-8", #文字コード。ちゃんと指定しないとUnicodeDecodeErrorが出たりする
delimiter=',', #区切り文字。csvは「Comma Splited Values」なのでcommaを指定。
skiprows=1, #先頭1行読み飛ばす(メタデータ(各列を説明する文字列)なので)
usecols=[1] #1行目が目的の値。0行目は日付データなので要らない
)
r = 自己相関(データ)
自己相関係数 = [r(日) for 日 in range(len(データ))]
plt.figure(figsize=(32, 8), dpi=500)
plt.xticks(np.arange(0, len(データ) + 1, 7))
plt.grid()
plt.bar(range(len(データ)), 自己相関係数)
plt.savefig('correlogram.png')
plt.show()
(以上)
横軸を7日間毎にとってグリッドを表示したところ、コレログラムが7日間周期でギザギザしていることが分かった。
このことからも、「コロナ陽性者は7日間ごとの波を繰り返している」ということが読み取れる。
5. 自己満足: 予測モデル作れないかなって
難しい理論や設定、調整とかほとんど無しで、過去のデータから未来予測をできないかなってやってみた。
5-1. コレログラム(自己相関関数)を利用したモデル
5-1-1. 仮説
- ある程度の短期間では、コレログラムは有意に変動しないだろう
- コレログラムが大きく変動しないように未来方向のデータを追加すると、追加されたデータは未来を予測する値となるのかもしれない
5-1-2. 仮説検証手順の説明
5-1-2-1. 手順1: 2020年7月までのデータだけに切り落としてコレログラムを作る
先頭198つのデータだけを取り出せばよい。
ソースコード
データ = np.loadtxt("pcr_positive_daily.csv", #ファイルパス
encoding="utf-8", #文字コード。ちゃんと指定しないとUnicodeDecodeErrorが出たりする
delimiter=',', #区切り文字。csvは「Comma Splited Values」なのでcommaを指定。
skiprows=1, #先頭1行読み飛ばす(メタデータ(各列を説明する文字列)なので)
usecols=[1] #1行目が目的の値。0行目は日付データなので要らない
)
西暦2020年7月までのデータ = データ[0:198]
西暦2020年7月までのデータによる自己相関関数 = 自己相関(西暦2020年7月までのデータ)
西暦2020年7月までのデータによる自己相関係数 = [西暦2020年7月までのデータによる自己相関関数(日) for 日 in range(len(西暦2020年7月までのデータ))]
plt.figure(figsize=(32, 8), dpi=500)
plt.xticks(np.arange(0, len(データ) + 1, 7))
plt.grid()
plt.bar(range(len(データ)), 西暦2020年7月までのデータによる自己相関係数)
plt.savefig('correlogram1.png')
plt.show()
(以上)
5-1-2-2. 手順2: そのコレログラムが変化しないように、2020年8月以降のデータを予測してみる
- 2020年8月以降のデータにランダムデータを置いてみる
- ランダムデータを含めてコレログラムを再度作り直し、それを「手順1で得たコレログラム」と比較してみる
- (1.)と(2.)を何十万回も繰り返し、その中で最も「手順1で得たコレログラム」と似たコレログラムになったランダムデータを「予測値」と呼ぼう
この実験には、次のようなプログラムが使える。
ソースコード
import numpy as np
def 最初の値たちから元データの推定(最初の値たち, 推定したいデータ長, 最大値, 最小値, 最高品質 = 0, 最高品質の仮データ=None):
if type(最初の値たち) != list:
raise Exception("最初の値たち はリストである必要があります。")
if len(最初の値たち) >= 推定したいデータ長:
raise Exception("推定したいデータ長は、len(最初の値たち)よりも大きい必要があります。")
自己相関関数 = 自己相関(最初の値たち)
自己相関係数 = [自己相関関数(ラグ) for ラグ in range(len(最初の値たち))]
def main():
仮データ = 仮データを作る(最高品質の仮データ)
仮データの品質 = 評価する(仮データ)
if 仮データの品質 > 最高品質:
最高品質_ = 仮データの品質
最高品質の仮データ_ = 仮データ
return [最高品質_, 最高品質の仮データ_]
return [最高品質, 最高品質の仮データ]
def 仮データを作る(最高品質の仮データ):
乱数たち = (np.random.rand(推定したいデータ長-len(最初の値たち))*(最大値 - 最小値)) + 最小値
if 最高品質の仮データ is None:
return np.array(最初の値たち + 乱数たち.tolist())
else:
差分 = [最大値 + 1]
while (max(差分) > 最大値) or (min(差分) < 最小値):
差分 = [0]*len(最初の値たち) + (乱数たち.tolist())
return 最高品質の仮データ + np.array(差分)
def 評価する(仮データ):
仮_自己相関関数 = 自己相関(仮データ)
仮_自己相関係数 = [仮_自己相関関数(ラグ) for ラグ in range(len(最初の値たち))]
return cos類似度of(仮_自己相関係数, 自己相関係数)
def cos類似度of(vec1, vec2):
vec1 = np.array(vec1)
vec2 = np.array(vec2)
return np.dot(vec1, vec2)/(np.linalg.norm(vec1)*np.linalg.norm(vec2))
return main()
(以上)
5-1-2-3. 手順3: 2020年8月以降のデータについて、予測と実際のデータとを比較する
(略)
5-1-3. 結果
データ[0,1,2,3,1,2,3,4,2,3,4,5](長さ12)に対して、長さ8の予測(併せたら長さ20)を行った。
周期4で1ずつ増えていく波が繰り返し現れつつ、この波の平均位置も1ずつ上がっている。
したがって、予測値は[3,4,5,6,4,5,6,7]となればよい。
手順1で次のコレログラムを得た。
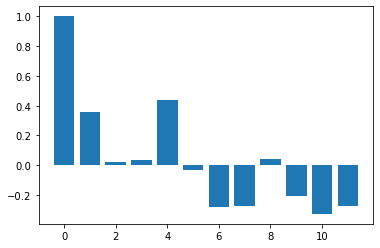
手順2で次のコレログラムを得た。
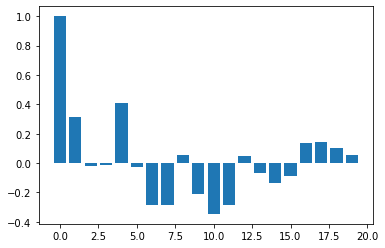
両コレログラム間のcos類似度は0.99788である。
しかし、手順2で得たデータを実空間でプロットすると次のようになる。