高校物理はオブジェクト指向で考えるべきだ

0.動機・目的

高校物理で力学を学ぶと、「何が何に働く何の力」かを考える必要がある。
例えば「釣り合いの力」と「反作用」の違いを説明する場合などがそうだ。
初学者に両者の違いを説明することを考えよう。
言葉(日本語、英語などのたいていの自然言語)で説明するととてもややこしく、しばしば混乱を招く。かといって図示による説明だけで済ませれば、その具体例に対する理解はできても、そこから抽象して本質の理解にまで至ることは期待できない。
そういった経緯で多くの初学者は、言葉と図を併用した説明が施される。
その結果、注意を一点(言葉または図のいずれか一つ)にしか向けられない初学者や、認知心理学におけるワーキングメモリ[1]が小さく、多くの情報を一度に処理できない初学者は他の初学者と比べて理解が著しく遅れることとなる。
こういった初学者を救済する一つの方法として、「何が何に働く何の力」を短くてかつ曖昧さのない記号列言語で説明することが挙げられる。この言語が実現すれば、初学者は適切な図を自らの理解のもと容易に描くことができるようになり、教える側は単に記号列を送信すればよいものとなる。
短くて曖昧さのない記号列言語とは、まさにプログラミング言語のことである。
特に「何がどのように(=何の力)何に働く」を考える今回の場合、「何」つまり「オブジェクト」に注目する必要があるため、オブジェクト指向プログラミングの言語を用いた説明が適切なのは明らかだ。
以上のような考えの下、本記事では高校力学の基礎をjavaの文法で説明し、その簡潔さを確認していく。

1.ニュートンの運動法則の説明

参考サイト[2]から、ニュートンの運動法則を引用する。

第一法則（慣性の法則）
　外的な力が加わらない限り、物体は静止或いは等速直線運動を続ける．
第二法則（運動法則）
　物体の加速度は、加えた力に比例し、その質量に反比例する．
第三法則（作用・反作用の法則）
　物体が互いに力を及ぼし合うときには、同一直線上で互いに逆向き・同一の大きさの力が働く．

但し別のサイト[5]では、第三法則における「力を及ぼしあう」という現象は、力が存在する限り必ず発生するということを「相互作用」という言葉を用いて述べていた。

1-1. 第一法則

第一法則は「加えた力が0である限り、物体の加速度は0である」と抽象することができ、これは第二法則の特殊な場合(つまり第二法則の一部)に過ぎない。議論[3]を読んでも第一法則には絶対静止空間の否定と慣性系の導入程度の意味しかなさそうなので、ここでは無視することとする。

1-2. 第二法則

第二法則を式で表すと、$a=\frac{F}{m}$であり、変形すれば運動方程式$ma=F$を得ることとなる。
加速度を与える者を$S$, 加速度を与えられる(得る)者を$O$と呼ぼう。
今、「AのCへのB」をA.B(C)と書くことにしよう。
$S$が$O$に与える加速度$a$はS.a(O)、
$S$が$O$に与える力$F$をS.F(O)とかける。
第二法則(から得られる運動方程式)は
O.m*S.a(O)==S.F(O)
と書ける。
確かにこの記法は$ma=F$と比較すれば複雑だ。しかし、$m$,$a$,$F$に関わる2つの物体が何であるかおよびその関係をすべて明示していることを考えれば、次のような日本語と比較すべきである。
「物体$O$の質量を$m$とする。$O$に$S$が加速度$a$を与えたとき、$O$には$ma=F$で計算される力$F$が加わる」

例として、かの有名な「木に生っていたリンゴが地球に引っ張られて落ちたことから万有引力が発見された」を考えよう。(図1.2.1)

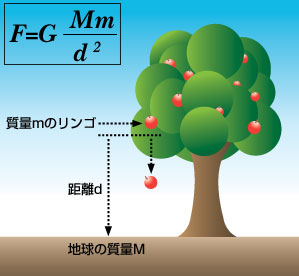
図1.2.1 万有引力[4]距離の説明が不適切。(本来dは地球の中心とリンゴの中心の間の距離だ。一度地面に落ちたリンゴを拾うには無限の力が要るなんてはずがない)

重力は次のように書くことができる。
(リンゴ.m)*(地球.g(リンゴ)) == 地球.重力(リンゴ)
万有引力は次のように書ける。
G*(地球.m)*(リンゴ.m)/(地球.中心同士の距離(リンゴ))^2 == 地球.万有引力(リンゴ) == リンゴ.万有引力(地球)
もちろん、地球.中心同士の距離(リンゴ)はリンゴ.中心同士の距離(地球)としてもよい。また^2は2乗を表すものとする
また重力の式と万有引力の式を比較すると、次のように地球の重力加速度$g$が地球とリンゴの距離によって変化しうるということが分かる。

重力の式より \\
(リンゴ.m)*(地球.g(リンゴ)) == 地球.重力(リンゴ) \\
万有引力の式より \\
G \frac{(地球.m)*(リンゴ.m)}{(地球.中心同士の距離(リンゴ))^2} == 地球.万有引力(リンゴ) \\
重力 == 万有引力とすると \\
(リンゴ.m)*(地球.g(リンゴ)) == G \frac{(地球.m)*(リンゴ.m)}{(地球.中心同士の距離(リンゴ))^2} \\
両辺を(リンゴ.m)で割ると \\
(地球.g(リンゴ)) == G \frac{(地球.m)}{(地球.中心同士の距離(リンゴ))^2} \\

(実際には重力と万有引力が厳密には同じものではない。地球の回転による遠心力を考えなければならなく、これによっても重力加速度は変化するが、これは第二法則とは別なのでここでは無視する。)

1-3. 第三法則

第三法則では、作用に対する反作用は、同一直線上で互いに逆向き・同一の大きさの力であり、互いに影響を及ぼしあうものとしている。これは次のように書ける。

作用をS.作用(O)とすると反作用はO.反作用(S)かつ反作用==-1*作用でなくてはいけない。

作用に対して反作用が必ず存在することも含めて記述するなら次のように書ける。

作用S.F(O)と同時に、同一直線上に反作用O.-F(S)が因果関係なく存在する。

「何が及ぼしている力であるか」や「何に及ぼされる力であるか」を意識せず、図示で誤魔化しているとこの関係を理解することは難しいが、オブジェクト指向で主語と目的語を明確にすることで、こんなにもシンプルに記述、理解できる。

また、「作用と同時に反作用が因果関係なく存在する」という言い方が独特に聞こえるかもしれないが、これは作用と反作用が完全に対等なペア(時間差もなければ因果関係もない)である[6]ということを述べるためである。すべての力は磁石の反発力・吸着力と同じように、「どちらが先ともメインとも言えない2つの組として生じる」のである。
例えば「人が壁を押す作用をすると、壁が凹み、弾力で元に戻ることによって壁からも人を押す反作用が働く」という説明は、弾力による時間差も生じるし、そもそも因果関係を認めているものなので完全な誤りだ。実際には(まるで)プラス同士かマイナス同士の電気(のように)、人と壁が同時に反発しあうのである。
_{(まるで～ように、といったが、本当に電磁気の反発が起こるのである。実際、電磁気が働かない物質とは大きさによらず私たちと「ぶつかる」ことなくすり抜けてしまうダークマターそのものである[7]し、量子力学で有名な「人が壁をすり抜ける確率は0ではない」も「『人の原子の電子』と『壁の原子の電子』の反発が起こらず、そのまま『透過する』場合」を考えることで計算されている[8]。)}

2. 力のつり合い

2-1. 説明

力のつり合いとはつまり、ある点での力のベクトルの足し算が0になることに他ならない。
物体$O$のある一点を$o$とすると、次のように書ける。
S.F((点) o) + S.G((点) o) == 0

「力のつり合い」を高校1年生の物理で習うのに対し、ベクトルは高校1年生の数学ではまだ習わない。したがって、「力ベクトルの和」などといった題名が付けられない。ただそれだけなのだ。これが成り立つとき、当たり前だが合力の大きさは0だから加速度が生じない。したがって物体は静止あるいは等速直線運動を続ける。

例えば地球が人を引っ張る力と地球が人を押す力はベクトルで足し算するとゼロベクトルになる。
これを書いてみると次のようになる。
地球.重力((点) 人) + 地球.垂直抗力((点) 人) == 0

2-2. 作用反作用の法則との違い

オブジェクト指向を使った記法では、作用反作用の法則と力のつりあいの違いがとても明白だ。
前者は
「S.F(O)があるなら同一直線上にO.-F(S)もある」
という法則であり、
後者は
「S.F(点o) + S.G(点o) == 0⇔加速度が0」
というものである。

3. 例題

3-1.

地球上の台の上に人がいる。それらはすべて静止している。また重力は使わず、万有引力で考えることとする。

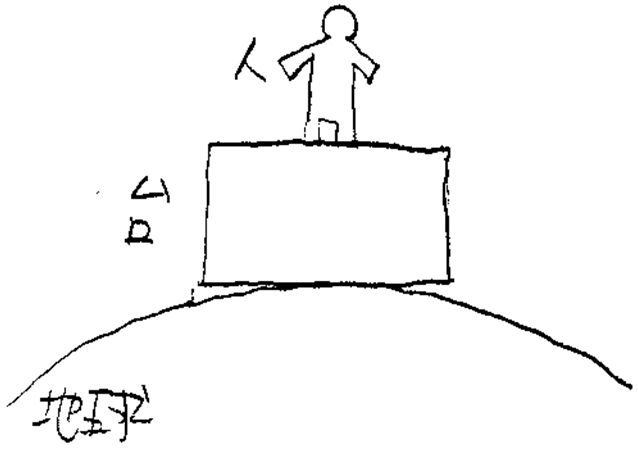
図3.1 静止系

3-1-1.

問題: 台にかかる力をすべて求め、その合力の大きさを求める式をいえ
→
S.F(台)で表されるものを求めればよい。今回台の他に考えている物体は地球と人だけなので、その2つがSとなり得る。
また静止して接している者は互いに引きあい(万有引力)、また押し合って(垂直抗力)いる。_{そしてすべてのものは引き合って(万有引力)いる。}
従ってまず引き合う力として地球.万有引力(台)と人.万有引力(台)がいえるだろう。
押し合う力も地球.垂直抗力(台)と人.垂直抗力(台)がいえる。
これらの力をすべて正とする場合(つまり力の向きを式で表現していない場合)、合力は次のように「上向きの力 - 下向きの力 = 0」という式で表すことができる。
人.万有引力(台) + 地球.垂直抗力(台) - ( 地球.万有引力(台) + 人.垂直抗力(台) ) == 0

3-1-2.

人が及ぼす力をすべていえ。またそれらを合わせた力が0になることを、作用反作用の法則を用いて証明せよ。
→
人.F(O)で表されるものを求めればよい。今回台の他に考えている物体は地球と人だけなので、その2つがOとなり得る。
よって、3-1-1と同様に考えて、
人.万有引力(台)、人.垂直抗力(台)、人.万有引力(地球)、人.垂直抗力(地球)が考えられる･･･と答えると惜しい。
というのも、人と地球は接していないため、人.垂直抗力(地球)はあり得ないのだ。
したがって、
人.万有引力(台)、人.垂直抗力(台)、人.万有引力(地球)
の3つを考えることとなる。
_{万有引力･･･すべての物同士
垂直抗力･･･接する物同士
と考えるとよい。}
また作用反作用の法則より、これら3つには反作用があり、それらはすべて人への力となる。(つまりO.-F(人)の形となる。)
人が静止しているという事実より、反作用の合力は0だから、向きを反対にしても、作用の合力は0だ。
_{いかがだろうか。力の主語と目的語を明らかにすることで、作用反作用の法則を用いた証明問題がいとも簡単に解けてしまうのだ。}

3-1-3.

地球が及ぼす垂直抗力の大きさを、垂直抗力以外の力の足し算や引き算で表せ
→
地球は台に接しているが、人には接していない。
したがって、地球.垂直抗力(人)はあり得ない。
そのため地球.垂直抗力(台)のみを考えればよい。
地球.垂直抗力(台)というのは台に働く力だ。したがって台に働く力のつり合いを考えてみよう。
これは3-1-1の通りだ。
よって
人.万有引力(台) + 地球.垂直抗力(台) - ( 地球.万有引力(台) + 人.垂直抗力(台) ) == 0
を変形して
地球.垂直抗力(台) == 地球.万有引力(台) + 人.垂直抗力(台) - 人.万有引力(台)
となる。･･･☆
次に人.垂直抗力(台)を求めよう。
3-1-2より、
人.万有引力(台)、人.垂直抗力(台)、人.万有引力(地球)
の合力は0だ。
「上向きの力 - 下向きの力 = 0」という式をたてると、
人.万有引力(台) + 人.万有引力(地球) - 人.垂直抗力(台) == 0
となるから、これを変形すると、
人.垂直抗力(台) == 人.万有引力(台) + 人.万有引力(地球)
となる。
これを☆に代入すると、
地球.垂直抗力(台) == 地球.万有引力(台) + 人.万有引力(地球)
となる。
もちろんこれでも正解であるが、作用反作用の法則を用いて、万有引力の大きさがお互いに等しいことより
地球.垂直抗力(台) == 地球.万有引力(台) + 地球.万有引力(人)
と書き換えたほうが分かりやすいかもしれない。

3-1-4.

垂直抗力の反作用を言え
→
ひっかけ問題に近い。垂直抗力の反作用は垂直抗力だ。別の力として後から生じるものではない。

4.非慣性系

気が向いたら加筆する

5.参考・注釈

[1]https://home.hiroshima-u.ac.jp/hama8/working_memory.html
[2]http://spinman.phys.se.tmu.ac.jp/Lecture/Mech/Nlaw/Nlaw.html
[3]http://hooktail.maxwell.jp/bbslog/23566.html
[4]http://spaceinfo.jaxa.jp/hayabusa/about/principle1_i.html
[5]https://ocw.hokudai.ac.jp/wp-content/uploads/2016/01/ScienceLiteracy1-2009-Text-03.pdf
[6]http://www.phys.u-ryukyu.ac.jp/~maeno/physgairon2018/lec2.html
[7]http://qed.hatenablog.com/entry/20140914/1410703205
[8]https://nazology.net/archives/8859