この記事は、執筆中の記事「位相空間と自然言語」の第1章である。

点列コンパクト、コンパクトなどの説明がやや不足しているなど不備もあるが、ご容赦いただきたい。

1. 位相空間のとても自然な導出

1-1. はじめに

僕はここのところ連日で37度以上の熱を出している。これが位相空間を理解しようと張り切った際の知恵熱によるものなのか、それとも知らない間にコロナウイルスに感染してしまったためなのかは、僕にもわからない。

はっきり言って位相空間は定義は簡単だ。「集合の集合」という概念がある程度理解できればその知識だけで位相空間を定義できる。しかしそこから本質を見出すことがあまりにも難しいのである。誰もが「やる気のない中学生」のような疑問―すなわち「こんなことを考えて何になる？」という疑問を持つようになる。普段から慣れ親しんでいる現実世界とのリンクが見えないから、議論を明確に理解できなくなる。それが位相空間の難しさだと思う。

ところで、位相空間論は、「抽象的すぎる」としてフランスの大学では教えなくなった[1]というエピソードを持つ。どうやら位相空間論の難しさはその抽象性にあるようだ。

そんな中、気が付いたことがあった。それは、
「いきなり抽象的な概念を理解しようとするのは無茶である」
ということだ。抽象的な概念とは、文字通り、対象から何かを抽出した後に生まれた概念なのである。実際には、「複数の対象から共通している特徴を抽出して生まれた概念」をいう。

対象(具体例)をかき集め、
共通するところを探し(抽出)、他は捨て(捨象)
名前を付ける

ことで抽象的概念が生まれる。

以上のような、覆し得ない因果関係(前後関係)が明確に存在するのである。

女性と男性の出会いに例えるのなら、

運命の出会いを見つけ、
子供が生まれ
名前を付ける

といった具合だ。

いきなり抽象的な概念を考えることなど、「現在では旦那(嫁)も決まっていないというのにタイムマシンに乗って未来へ行き、自分の子供の顔を見に行く」ようなものである。これでは、彼女(彼)が自分の娘(息子)であることなど、実感がわくわけがないのである。順番をはき違えるから、連続する因果を納得いくように追うことができず、「因果ワープ」させられ、理解不能に思えてしまうのである。

しかし、具体→抽象の順に考えるのが常に正解とは限らない。というのも、「抽象」は「一般」の類義語で、「具体」は「特殊」の類義語だからである。

例えば、「ベクトル集合」は「集合」の具体例であるが、おそらく「集合」の方が理解しやすいのではないだろうか。

要は、難しい概念を新たに学ぶときは、具体⇔抽象や拡張などの関係があるはずなので、そのつながりを追いながら、わかりやすいものから順に考えていくのが良いということである。

考えるべき順番は、
「集合」→「ベクトル集合」→「ベクトル空間」→「ユークリッド空間」→「距離空間」→「位相空間」

である(と思う)。本稿ではこの順で解説していく。

1-2. 集合

1-2-1. 定義

集合とは、「モノ」を集めた「モノ」のことである。

例えば、色の三原色を集めた集合は
$$\{シアン, マゼンタ, イエロー\}$$

のように書くことができる。

この時、シアンやマゼンタやイエローのことをそれぞれ集合の「元」(げん)という。

元の順番は入れ替わっていてもよい。

つまり
$$\{シアン, マゼンタ, イエロー\}=\{マゼンタ, シアン, イエロー\}$$
である。

このように元の個数がある程度小さいときは、すべて列挙することで集合を表現することができる。これは集合を外延的に定義したという。

一方、元の個数が無限個ある場合、外延的な定義は当然無理だ。

例えば、正である3の倍数を集めた集合とか。
まさか$\{3,6,9,12, ...\}$と書くわけにはいくまい。_{_{(実際にはわかりやすさを優先してこのように書くこともあるのだが。)}}
この場合は、$\{3n|n\in\mathbb{N}\}$とか$\{n|\frac{n}{3}\in\mathbb{N}\}$という書き方をする。ちなみに$\mathbb{N}$は自然数の集合だ。
このように、$\{記号|記号の説明\}$みたいに集合を定義するのを内包的定義という。

1-2-2. 「含む」とは

集合には2種類の「含む」が存在する。
例えば、$\{a,b,c,d,e\}$は$a$を「元として」含んでいる。
このような関係は$a\in\{a,b,c,d,e\}$とかかれる。
また、$\{a,b\}$は明らかに$\{a,b,c,d,e\}$の一部である。
$\{a,b,c,d,e\}$は間違いなく$\{a,b\}$を含んでいるのであるが、
「元として」は含んでいない。「一部として」含んでいるのである。
この関係は$\{a,b\}\subset\{a,b,c,d,e\}$とかかれ、$\{a,b\}$を「部分集合」という。

実は、真部分集合なるものを考えたとき、大学数学と高校数学では記号「$\subset$」の意味が若干異なるのであるが、本稿では解説しないことにする。

1-2-3. ベクトル集合

ベクトルを元とする集合を考えることもできる。
_{_{(「ベクトルに対しては空間を考えるべきで、集合を作るのはベクトルではなくて座標だろ」という突っ込みもあるかもしれないが、筆者はその辺は「流儀の違い」くらいに考えている。なぜなら、「ベクトルとは数の順序組である」という説明が許されたりするからである。つまり、ベクトルが演算法則を内在しているべきかについては議論が分かれているのが現状だ。)}}

例えば、
$$\{(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)\}$$
などがそれである。
このベクトル集合の各元($(0,2)$など)は2次元ベクトルだ。
そしてこの2次元ベクトルの成分はどちらも$\{0,1,2\}$の元である。
だったら$\{0,1,2\}$を使って上のベクトル集合を表現してもよさそうである。
ここで役に立つのが直積集合の考え方である。
$\{0,1,2\}\times\{0,1,2\}$と書くことで、$\{(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)\}$を表現したとみなすのである。
また、「同じ数を掛け算する操作は、指数を使ってもっと簡単に表せる」ことになぞらえ、
$\{0,1,2\}^2$と書くこともできる。

練習問題: 3次元実数ベクトルの集合を2文字で表現せよ。ただし実数の全体集合は$\mathbb{R}$で表すことができる。
→$\mathbb{R}^3$

1-2-4. ラッセルのパラドクス

1-2節の最後に、集合には「型」があるという話をしよう。結論から言ってしまえば、「1次元配列の配列は2次元配列となり、1次元配列とは明らかに別物である」のと似た話である。_{_{(もっとも、postgreSQLでは同一視してしまうのであるが)}}
配列でこうなのだから集合でも同じなのだ。

ラッセルのパラドクスは背理法の文脈で出てくるパラドクスである。

要は、「安直なルール」に対してラッセルのパラドクスが

「いや、ほら。そのルールだとさ、ここが矛盾するぜ？」

と背理法で論破することで、そのルールが不適切であることを証明した。こうして「新たなルール」が作られたのである。

安直なルール

(※このルールは後に論破され破綻する)

集合は「モノの集まり」というモノだ。

当然「集合の集合」を考えてもよさそうだ。

「集合の集合は、『単なる』集合である」ってことにしよう！

ラッセルのパラドクス

「安直なルール」に従えば、
$$\{x|xは自分自身を元としない集合\}$$
を考えてもよいということになる。この集合を$A$と呼ぼう。

さて、$A$自身は$A$の元といえるだろうか。
$A$を$A$の元と仮定するとき、まさにこの仮定によって$A$が「自分自身を元とする集合」となった。
思い出せ、$A$とは「自分自身を元としない集合」の集合だった。
そのような集合に、「自分自身を元とする集合」である$A$は含まれてはならない。
故に、$A$は$A$の元たりえない。

ほう、$A$は$A$の元ではないのだな？確かめてみよう。
$A$を$A$の元でないと仮定するとき、まさにこの仮定によって$A$は「自分自身を元としない集合」となった。だが同時に$A$は「自分自身を元としない集合」の集合だ。
と、いうことは、「自分自身を元としない集合」である$A$を、$A$に含める必要がある。
故に、$A$は$A$の元でなくてはならない。

みよ。「$A$は$A$の元である」は否定されるが、しかしそれもまた否定される。
このようにして、「$A$は$A$の元である」の真偽値が定められない。矛盾だ。
これは、「『$A$は$A$の元である』という命題」自体が存在しないことを表している。(命題には真偽が定まる必要があるため)

新たなルール

先ほどの議論で「安直なルール」が悪い奴だと言った。

では、安直なルールの、具体的にどこに非があったのだろう。

筆者のような凡人は「自己言及を許したこと」と発想して片づけるが、ラッセルはそれよりずっと深い議論を展開した。

集合の集合を『単なる』集合としたことに非を見出したのだ。

こうして_{_{(厳密には「こうした背景もあり、」)}}生まれたのが型理論[2]である。

ちなみにこの「型」というのはプログラミング言語等における「型」とも関係が深いそうだ_{_{(postgreSQLにおける「配列型」では「型」の構造が大きく変わっている気もするが)}}。

ラッセルが言ったのは、「$a\in A$のとき、$a$と$A$が異なる型を持つ」ということである[3]。なるほど、こうすれば$x\in x$なんて議論はそもそも成立しない。型が異なるのだから。

厳密さに欠けるのかもしれないが、[3]を参考に詳しく説明してみる。

集合とは見れないものを「0階である」とみる。

0階なものを元とする集合を「1階の集合」と呼ぶ。

同様に$n$階の集合を元とする集合を「$n+1$階の集合」と呼ぶ。

1-3. 空間

1-3-1. ベクトル空間

ベクトル空間とは、ベクトル集合にベクトル演算というものを定めたものである。

以下、このことの詳細を述べる。

いきなりだが、オブジェクト指向プログラミングをしてみよう。

お題は「ベクトル集合$\mathbb{R}^3$を使って、ベクトル演算を行う」ことである。

お題は「ベクトル集合$\mathbb{R}^3$を使って、ベクトル演算を行う」ことである。
(プログラマ向けに詳細を述べておくと、フィールドはたった一つのベクトル集合$\mathbb{R}^3$でprivate、またメソッド_{_{(本稿では「関数」と呼ぶ)}}はすべてpublicとする。またコンストラクタ_{_{(本稿では「不思議な関数」と呼ぶ)}}は集合の元を特定するためのsetterの役目を果たすものとする。)

直感的に書くと、次のようになる。
(R^3は$\mathbb{R}^3$のように読み替えてほしい)

プログラム "三次元ベクトル空間" 
{
    R^3 a;
    //コメント: R^3のとある元に「a」という名前を与えている

    aを特定する不思議な関数(R x, R y, R z) = 
    //コメント: 引数としてRの元を3つ受け取り、順にx,y,zと名付ける。
    {
        a[1] = x; a[2] = y; a[3] = z;
        //コメント: 「a[i]」はベクトルaの第i成分のこと。
    }

    関数 加算(R^3 b) =
    {
        a[1] = a[1] + b[1];
        a[2] = a[2] + b[2];
        a[3] = a[3] + b[3];
    }

    関数 掛け算(R r) =
    {
        t = new 三次元ベクトル(0,0,0);
        u = deepcopy(a); //コメント: uにaを一時的に保存
        r回繰り返す
        {
            t = a.加算(t);
            a = deepcopy(u); //コメント: aをuから復元
        }
        a = t;
    }
}

上のプログラムでは$\mathbb{R}^3$の元$a$を使って、$\mathbb{R}^3$の元$b$を足し算したり、$\mathbb{R}$の元$r$を掛け算したりしている。しかも、足し算や掛け算の結果は必ず$\mathbb{R}^3$の元となる(このことは$a$に再代入していることから容易に確認できるだろう)。

このプログラム全体を集合$\mathbb{R}^3$とみることはできるだろうか？

無理に決まっているじゃないか。
なぜならこのプログラムは
$$\{\mathbb{R}^3, 不思議な関数, 加算関数, 掛け算関数\}$$
みたいな構造を持っているのだから。

そうなのだ。$\mathbb{R}^3$に対して「演算を定義しよう」などと考えた時点で、
それ全体は「$\mathbb{R}^3$を含む、もっと大きな何か」になっているのである。

考えに考え抜いた結果、数学者たちは、関数をまとめ、さらに「集合とは別物だ」と考え、
$$(\mathbb{R}^3, ベクトル演算)$$
のように表すことにした。そしてこれを「ベクトル空間」と呼ぶことにした。

以上の議論からわかる通り、空間とは(集合, 演算)のことである。集合が基本型(primitive型)、演算がメソッドならば、空間はクラス型のオブジェクトなのである。

とはいえ、実際には、「…ここで、ベクトル空間$\mathbb{R}^n$を考えると…」なんて言い方をすることがほとんどである。むしろ「…ここで、ベクトル空間($\mathbb{R}^n$, ベクトル演算)を考えると…」という言い方をしてくれている例をほとんど見かけない。きっと、「空間と集合は別物」という事実を明示することよりも、「(集合, システム)という表現を用いれば、その『システム』について説明しなくてはならず、面倒」という事実が優先された結果であろう。まあ、この辺りはあまり神経質にならないほうがいいだろう。

ちなみに「この辺り」の詳しい説明がwikipedia[4]にある。

1-3-2. ユークリッド空間

ユークリッド空間[5]は「直感的な空間」そのものである。

_{_{蛇足すると、ベクトル空間との本質的な違いはあまり大きくない。}}

実はベクトル空間の定義は、「足し算や(実数との間の)掛け算の結果が、同じベクトル集合の元となるような足し算、掛け算をベクトル演算として持つ」ことのほかに、

「足し算や掛け算の内容が、ある一定の条件を満たす」ということを要求している[6]。逆にその定義を満たすものである限り、どんなへんちくりんな足し算や掛け算を定義してもかまわないのである。

一方、ユークリッド空間ではそもそもベクトル演算を定義に持つわけではない。まあ実際はベクトルとの関わりは深い(位置ベクトル、ベクトルの絶対値などを考えればわかること)のであるが、ここでいうベクトルは、それこそ位置ベクトルを計算できるようなベクトルである必要がある。すなわち「へんちくりんな足し算、掛け算」ではダメなのだ。

任意の場所が、実数の組み合わせ(座標や位置ベクトル)で表現される。

2地点の距離がL2距離(ユークリッド距離)により計算可能である。

例えば2次元ユークリッド空間$(\mathbb{R}^2, L2)$上の点(2,5)と点(9,4)の距離は
$$L2((2,5), (9,4)) = \sqrt{|2-9|^2+|5-4|^2} = 4\sqrt{3}$$
と計算される。

練習問題: オブジェクト指向による二次元ユークリッド空間(R2,L2)のクラスを完成させよ(意味が捉えられていればよいので、指数を表す記号やその他は適当に定義してよい)

プログラム "二次元ユークリッド空間" 
{
    R^2 a;

    aを特定する不思議な関数(R x, R y) = 
    {
        a[1] = x; a[2] = y;
    }

    関数 距離(R^2 b) =
    {
        ????//この部分に当たるコードを答えてほしい
    }
}

→
$\sqrt{|a[1]-b[1]|^2 + |a[2]-b[2]|^2}$
もちろん、これと同じ意味が表現できていればよい。

ちなみに、このプログラムを利用して、(2,3)と(5,7)の距離を求めたければ、

new 二次元ユークリッド空間(2, 3).距離(5, 7);

のようなコードを入れると、距離5が求められる。

1-3-3. 距離空間

1-3-2節で解説したユークリッド空間において、$L2$は距離を求める関数である。

数学者たちは、この「距離を求める関数」をいじくれないか考えた。

要は、「各成分の差を2乗した総和を、1/2乗する」のとは異なる方法による距離も考えたくなったのである。

そうして出てきたのが、「距離空間」という概念である。

実は1-3-2節の練習問題は、「距離空間のクラスを示すから、????を埋めることで具体化し、ユークリッド空間にせよ」という問題としても解釈できる。

ユークリッド空間は距離空間の「一例」である。

ということは、「ユークリッド空間以外の距離空間」が存在する。

例えばマンハッタン距離($L1$)による距離空間$(\mathbb{Z}^2, L1)$を考えることも可能だ。
例えば(マンハッタン距離による)2次元距離空間$(\mathbb{Z}^2, L1)$上の点(2,5)と点(9,4)の距離は
$L1((2,5),(9,4))=|2−9|^1+|5−4|^1=8$

と計算される。これは任意の座標(整数, 整数)上に交差点があり、その間が道路でつながれているような「網目のような道」(京都やマンハッタンの市街地を想起せよ)とき、車が走る最低距離に対応している。

もっとも、L2距離(ユークリッド距離)やL1距離(マンハッタン距離)は次のように一般化できる。
$$Lp((2,5), (9,4)) = (|2-9|^p + |5-4|^p)^\frac{1}{p}$$
Lp距離において、L1距離やL2距離のほかに特筆すべきものにはL∞距離(チェビシフ距離)が挙げられる。

また、距離を求める関数$d(x,y)$には条件がある。次の4つである。

$d(x,y)≥0$ (負の距離はダメ。必ず0以上の実数)
$d(x,y)=0⇔x=y$ (自身への距離は0, 他者への距離は正)
$d(x,y)=d(y,x)$ (自身と相手への距離は、相手と自身への距離に等しい)
$d(x,y)+d(y,z)≥d(x,z)$ (「寄り道したら近道」はあり得ない。)

練習問題2: なるべく計算が簡単な距離関数を提案せよ。実用性などは考えなくてよい
→

もっとも計算が簡単なのは、「常に同じ値を返す」関数だ。(計算を行わない)
しかし、それは$d(x,y)=0⇔x=y$を満たさない。
仕方がないので場合分けをする。
$$d(x,y)=\left\{\begin{array}{aaa}0 && x=y \\ 1 && x \neq y\end{array}\right.$$

実はこれでもう答えである。

実際、この定義は
$d(x,y)\geq 0$
$d(x,y)=d(y,x)$
$d(x,y)+d(y,z)\geq d(x,z)$
にも違反しない
ちなみに、このような距離を持った距離空間は「離散距離空間」と呼ばれる。

1-4. 距離空間から位相空間へ

位相空間とは、距離空間から距離の概念を取り除いたものである。
距離空間は位相空間の一例であるのだが、もちろん「位相空間ではあるが距離空間ではない」ような空間も存在する。とはいえ、そのような空間をイメージするのは難しい。
そこで、位相空間論を
「距離空間について考えるのだが、『距離』について考えたら負け」というゲーム
であると考えてはどうだろう。要は、距離空間について、『距離』を使わずに如何に深く考えることができるかを競うのである。
「コーヒーカップとドーナツが同相(位相同型)」というのは著名な例であるが、これは「『距離』を持ち出したら負けになってしまうせいで、誰も両者の違いを説明できない」
ということである。

このゲームでハイスコアを叩き出すためには、距離空間の性質をとことん知っておく必要がある。
距離空間の性質の中で、「実は距離を使わなくても説明できてしまう」ものがあれば、それが位相空間の性質となる。そのような性質を挙げれば挙げるほどスコアが上がる。

というわけで、1-4節では、まず1-4-1節で距離空間の性質を徹底的に調べ、それから1-4-2節にて「距離を考えたら負けというゲーム」である位相空間論を展開する。

1-4-1. 距離空間の性質

位相空間を考えるための、距離空間の性質については[7]などを参考とした。

1-4-1-1. ε近傍(開球)―「近く」とは

本稿執筆当時は「新型コロナウイルス」なるものが流行っていた。

集団感染を防ぐためのアイデアとして、「三密を避けろ」と声高に叫ばれた。
三密とは、密閉、密接、密集を避けよということである。

密接とは、「人々が互いに近づきすぎてはいけない」ということなのだが、
具体的にどのような時、「近づきすぎている」と判断できるのだろう。
一説によれば、「人が、互いに半径2メートル以内に近づくこと」だそう。

このように、「近さ」の基準を明確にしたいときは、「半径$\varepsilon$以内(または未満)」という表現が有効なのである。
距離空間上の点$p$(空間の元は、一般に「点」というそうだ。)の、「近く」を集めた集合を考えるときも、「点$p$からの距離が$\varepsilon$未満の点を集めた部分空間」を考えればよい。
そのような部分空間を、「点$p$の$\varepsilon$近傍」または「中心$p$、半径$\varepsilon$の開球」といい、(本稿では)$U(p,\varepsilon)$と書くことにする。

練習問題1: 二次元ユークリッド空間において、$U((3,4),5)$を求めよ。
→点(3,4)の半径5未満の点を集めた集合を答えればよい。

まず、中心(3,4)、半径5の円の方程式を求めると、
$(x-3)^2+(y-4)^2=5^2$
である。よって、半径5未満の領域は
$(x-3)^2+(y-4)^2<25$
で示されるので、
$\{(x,y)|(x-3)^2+(y-4)^2<25\}$
が答えとなる。

練習問題2: 距離空間において、任意の点pのε近傍に含まれる元u(∈U(p,ε))のε近傍の和集合は、必ず点pのε近傍に含まれると考えることができるという事実を説明せよ
→
要は、任意の$\varepsilon_1$や$\varepsilon_2$に対し、
$$\bigcup_{u\in U(p,\varepsilon_1)}U(u,\varepsilon_2)\subset U(p, \varepsilon_3)$$
とみれるような$\varepsilon_3$が存在することを示せばよい。
まず、$U(p, \varepsilon{1})$の領域は、中心$p$, 半径$\varepsilon_1$の「円」_{_{(実際にはユークリッド空間とは限らないが)}}の領域に一致する。

そのような円内の任意の点$u$に対し、
$U(u,\varepsilon_2)$の領域は、中心$u$、半径$\varepsilon_2$ の「円」の領域に一致する。
この円内の任意の点を$v$と呼ぼう。

距離の条件(1-3-3節)の一つ
$d(x,y)+d(y,z)≥d(x,z)$
より、
$d(p,u)+d(u,v)≥d(p,v)$
が成立する。
$d(p,u)$の最大値は$\varepsilon_1$
$d(u,v)$の最大値は$\varepsilon_2$
だから、$p$の$\varepsilon_1$近傍の元$u$の$\varepsilon_2$近傍の元$v$と、$p$の距離は高々$\varepsilon_1+\varepsilon_2$
故に、$v$の和集合は$p$の$\varepsilon_1+\varepsilon_2$近傍に含まれる。

1-4-1-2. 「境界」とは

新型コロナウイルス騒ぎが特に深刻だったころ、各都道府県や政府は「県境をまたぐ移動」を自粛するよう求めた。

さて、「県境をまたぐ」とはどういうことだろう。

それは、「1つの物体が、2つの県に同時に存在する」ことである。

その物体の大きさは関係ない。人間だろうと、微生物だろうと、県境をまたぐときは、2つの県に同時に居るのである。

これは、$\varepsilon$近傍においても同じことが言える。
点$p$の$\varepsilon$近傍が、どのような正の数$\varepsilon$に対しても、「神奈川県と静岡県の両方に存在する」といえるとき、点$p$は神奈川県と静岡県の県境上の点であるといえる。

以上を数学の言葉で言いかえれば、距離空間上に境界という概念を定義できる。
集合$A(\subset X)$に対して、どのような正の数$\varepsilon$に対しても点$p(\in X)$の$\varepsilon$近傍が、
$A$に対しても補集合$X-A$に対しても共通部分を持つとき、
$p$を「$X$における$A$の境界点」という。

練習問題3: 全体集合を$X$とし、$A\subset X$とする。$A$の境界点を集めた集合$B(A, X−A)$は$A$の部分集合または$X−A$の部分集合というべきだろうか。整合性のある議論を行え。
_{_{但し、$B(A, X−A)≠ϕ$ かつ $B(A, X−A)⊂X$とし、

$B(A, X−A)$は矛盾した集合ではないものとする。}}
→
$A$の境界点を集めた集合$B(A, X−A)$の取り扱いについては
_{_{仮定より$B(A, X−A)$は矛盾した集合ではないため}}
$b∈B(A, X−A)$とするとき、bは
(i)$A$にも$X−A$にも含まれない
(ii)どちらにも含まれる
(iii)どちらか一方に含まれ、片方には含まれない
の3通りのいずれかになる。

(i)と仮定すると
$(X=)A∪X−A=X−b(A, X−A)$となってしまう。
故に、(i)ではない。
(ii)と仮定すると
$(ϕ=)A∩X−A=b(A, X−A)$となってしまう。
故に、(ii)でもない。

故に(iii)とみるほかない。

_{_{ちなみに、小文字で書いたところは、「境界は概念に過ぎない！実在するものではない！」と考えている人(何を隠そう、本稿執筆時の僕である)のための注意書きである。

「境界点」という点は、点として実在するではないか。もっと言えば、そう定義したではないか。少なくとも数学的に距離空間を議論する場合において、境界は概念ではなく、実在する部分集合として「定義した」ものなのだ。}}

1-4-1-3. 「開集合」と「閉集合」

さて、練習問題3の結論より、
$A$と$X−A$の境界点は、$A$または$X−A$のいずれか一方に属することがわかった。

さて、すべての境界点が$A$に属していると考え、
$X−A$には境界点が1つも含まれていないと考えることもできる。
このような時、$Aを$閉集合、$X−A$を開集合と呼ぶ。
つまり、境界点が全く含まれない集合を開集合、すべての境界点が含まれる集合を閉集合呼ぶわけだ。

練習問題4: 開集合の補集合が必ず閉集合であり、閉集合の補集合が必ず開集合となることを説明せよ。

→

開集合とは、境界点を持たない集合のことである。

つまり、すべての境界点は、開集合の補集合内に存在する。
また、すべての境界点を持つ集合とは、閉集合のことである。

故に、開集合の補集合は閉集合である。

閉集合とは、すべての境界点を持つ集合のことである。

つまり、開集合の補集合内には境界点は存在し得ない。

また、境界点を持たない集合とは、開集合のことである。

故に、閉集合の補集合は開集合である。

練習問題5: 開集合でも閉集合でもない集合の例を挙げよ。
→
ある境界点は$A$に、別の境界点は$X−A$に含まれるとすれば、$A$や$X−A$は開集合でも閉集合でもない集合

1-4-1-4. 点列

点列とは、数列の拡張である。

数列とは、定義域が自然数な1変数関数のことをいう。
これに対し点列とは、定義域が自然数で、値域が距離空間上の点であるような関数(写像)のことをいう。

そのため、数列の極限(入力を限りなく大きくしたときの出力値)が議論可能なのと同じように、点列に対しても極限や収束といった概念を考えることができる。

練習問題6: ユークリッド空間の距離が多変数関数の意味で連続であることを、点列の収束を用いて示せ。ただし、ユークリッド空間では極座標変換が可能であるという事実は、証明なしに用いてよい。
→
ユークリッド空間$\mathbb{R}^n$はどのように平行移動しても全く同一視できるユークリッド空間だ。
これを利用し、原点で連続であることを示せば、ユークリッド空間が任意の点で連続であることを示せる。

原点を極限とする点列の一般項を$o_m$と書くことにする。
任意の点$a$に対し、一般項$x_m=o_m+a$な点列は、$a$を極限とする点列である。
さて、距離が多変数関数の意味で連続とはどういうことか。
そもそも多変数関数における$(a,b,…)$での連続とは、
$(x,y,…)$をどのように$(a,b,…)$へ近づけても$f(x,y,…)$が$f(a,b,…)$へ近づくことをいう。
今回は、$(x_m,a)$をどのように$(a,a)$へ近づけても、$d(x_m,a)$が$d(a,a)$つまり0へ近づくこと(※)をいう。
今回、$d(x_m,a)=d(o_m,O)$が明らかなので、($O$は原点あるいは0ベクトル)
$o_m$がどのように定義されていても$d(o_m,O)$が0へ近づくことを示せば、
(※)が直ちに示される。
さて、$o_m$は、$n$次元ユークリッド空間上の点なので、
極座標変換が可能である。
その詳しい説明は拙著[9]に譲るが、
原点からの距離$r$および角度を指定するためのパラメータ$\theta_2～\theta_n$を使って表現できる。
このとき、$m→∞$とすれば、距離$r=d(o_m,O)$は0へ収束する。(その際の角度パラメータの振る舞いは$o_m$の定義により異なる。) 　

参考:[8]

1-4-1-5. 部分列

ある点列$A$から、一部の値たちを取り出し、順番を維持して(取り出されなかった値のために空欄となっている箇所は詰める)新しい点列$B$を作ることを考えよう。
このとき、$B$を$A$の部分列という。

練習問題7: 点列$A$から、一部の値たちを取り出し、並べた列を$B$と呼ぼう。
$B$が$A$の部分列であるための条件を議論せよ。
→
部分列は点列であり、点列の定義域は自然数全体である。
したがって部分列の定義域もまた自然数全体である。
つまり、直感的な言葉で言えば、点列$A$から値を(順番を維持しながら)無限個取り出してくる必要がある。
$A$の一般項を$a_n$, $B$の一般項を$b_n$ というとき、
$b_n=a_{c_n}$ となるような数列$C:\mathbb{N}→\mathbb{N}(一般項c_n)$が存在する必要がある。
また、$n<m$ならば$c_n<c_m$ の必要がある。

練習問題8: 点列$A$が発散(振動を除く)または収束するとき、$A$の任意の部分列の極限を求めよ。
→
点列$A$の任意の部分列を$B$と呼ぼう。
練習問題7の議論より、
$b_n=a_(c_n ) (c_n:\mathbb{N}→\mathbb{N} (n<mならばc_n<c_m ))$と表すことが可能である必要がある。

$\lim_{n→∞}⁡ a_n $ を$a_∞$とかく場合、
$c_n$ の定義より、$n≤c_n$ なので、
$b_n=a_{c_n}→a_∞$
といえる。すなわち、「振動しない限り」発散の仕方や収束先は一致する。

練習問題9: 点列$A$が振動するとき、$A$の任意の部分列の極限を求めよ。
→
$\lim_{n→∞}⁡a_n$ を$a_∞$ とかくことにする。($b$も同様)
$a_∞$ が(たとえ$∞$の記号を用いても)定まらないので、何とも言えない。

例えば
$n→∞$のとき、
$$a_n\rightarrow\left\{
\begin{array}{aaa}
\alpha && nが奇数　\\
\beta && nが偶数
\end{array}
\right.$$
のように振動するものとしよう。
部分列$b_n$の取り方を工夫することで、
$b_∞=α$とすることも、
$b_∞=β$とすることも、
$$b_n→\left\{
\begin{array}{aaa}
\alpha && nがある条件を満たす場合 \\
\beta && それ以外
\end{array}
\right.$$
とすることも可能になってしまう。

1-4-1-6. 点列コンパクト

参考:[10]

距離空間$(X,d)$を考えよう。
$(X,d)$上における任意の点列が必ず$(X,d)$上の点に収束する部分列を持つとき、
$(X,d)$は点列コンパクトであるという。

1-4-1-7. 被膜とコンパクト

参考:[11]

距離空間$(X,d)$を考えよう。
$X$の開集合な部分集合をいくつか集めた2階の集合$\mathfrak{O}$を考える。
_{_{また本稿では$n$階の集合が$n-1$階の集合を元として含むことを示すとき、}}

\in_n
または
_{n-1}\in

_{_{という記号を使ったり使わなかったりする。}}

今、$\mathfrak{O}$の各元の和集合
$$U=\bigcup_{O∈_2 \mathfrak{O}}O$$
を考える。
$U=X$であるとき、$\mathfrak{O}$を$(X,d)$の被覆という。
また、被覆$\mathfrak{O}$に対しても、その元を有限個選んで集めた$O′$もまた被覆と見れるとき、
$(X,d)$はコンパクトであるという。

練習問題10: 2次元ユークリッド空間の部分空間であって、コンパクトではない例$A$とコンパクトである例$B$をそれぞれ図示せよ。(被覆の説明も図を用いて行え)
→
次のような$A$を考える。

ちなみにふちがボケているのは、開集合であることを示す演出のつもりである。

そして、その部分集合(開集合)をいくつか(有限個※)持ってきて、
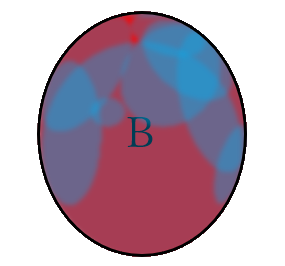
例えば次のような感じにする。

この図は、「『開集合の2階集合$\mathfrak{O}$の元』をすべて表示したもの」とみることができる。
Aも同時に表示すると、

のように$\mathfrak{O}$の元の和集合が、$A$と「ほとんど」一致した。
完全一致かどうかはまだわからないが、
もし完全一致であったとするなら、$\mathfrak{O}$を$A$の被覆という。

結論から言うと、残念ながら$\mathfrak{O}$は被覆ではない。
$\mathfrak{O}$は$A$の部分集合である以上は境界を覆うことができない。
$\mathfrak{O}$が「$A$の境界まであと1歩」のところまで$A$を覆ったとしても、
$A$の点自体が「$A$の境界まであと0.1歩」のところにも存在するのだ。
このいたちごっこは永遠に続いてしまう。
一般化して言うと、
$\mathfrak{O}$が「$A$の境界まであと$ε(>0)$歩」のところまで$A$を覆ったとしても、
$A$の点自体が「$A$の境界まであと$(ε>)δ(>0)$歩」のところにも存在するのである。
※を思い出せ。$\mathfrak{O}$はこの「永遠に続くいたちごっこ」に有限回しか挑戦できない。
したがって、$\mathfrak{O}$は$A$を覆いきれず、諦めることとなるのだ。

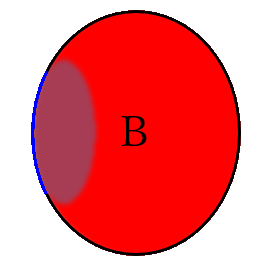
しかし、次のような閉集合$B$に対しては、$\mathfrak{O}$は被覆となることができる。

こうすれば、$\mathfrak{O}$は境界をも、有限個の開集合にて覆うことができる。

補足:

しかし、一つ疑問が残る。「開集合が境界で終わる」というのはいかがなことなのだろうか。この疑問をわかりやすくするために、開集合を一つだけ残し、後は消して表示してみる。

青く示したところは「開集合が持つ境界」というとてもおかしな部分である。
これは、$B$を全体空間とみることで解決される。
確かに$B$はユークリッド空間の部分空間なのだが、「開集合」とか「閉集合」とかを議論するうえでの全体集合と捉えてほしい。
こうすると、変な開集合の補集合を考えたとき、次のようなる。

すなわち閉集合なのだ。
変な集合の補集合が閉集合ということは、変な集合はやはり開集合としてみてよいのである。このように、「全体集合は開集合か空集合か」を考えるとき、不思議なことが起こる。
これは、全体集合と空集合が「開かつ閉集合」(clopen-set)とみなくてはいけないことに起因する。詳しくは練習問題14で議論する。

1-4-1-8. 有界

参考:[12]

ある$m(>0)$を探してくる。任意の点$a(∈X)$, $b(∈X)$に対して$d(x, a)≤m$が成り立つとき、$X$は有界であるという。

距離空間の部分空間$A$が有界であるとき、有限の半径$ε$を持つ$ε$近傍にて$A$が覆える。

練習問題11: 任意の集合を有界にしてしまうような距離を提案せよ
→
1-3-3節の練習問題2に示した「離散距離」が一例。
2点間の距離は0または1なので、$m=1$とすれば有界の定義を満たす。

1-4-1-10. 開基と位相

1-4-1-7節では、開集合の2階集合$\mathfrak{O}$を考えた。
ここでも、$\mathfrak{O}$を考える。
距離空間において、任意の中心点や半径の開球(近傍)の2階全体集合$\mathfrak{O}′$のことを開基という。
また、開基の任意の元を任意個取り出してその和集合を新たな元として追加することを考える。これを繰り返して出来上がる2階集合$\mathfrak{O}$のことを位相という。

練習問題12: 位相が、任意の開集合を元としていることを証明せよ。

→

(証明)

開基は、各点における任意の半径を持つ開集合を集めた2階集合なので、任意の点を含み、別の任意の点を含まない開集合が、必ず開基の元として存在する。
したがって、開基の元を適当に選んで足し合わせることで、任意の個数の任意の点のみからなる集合$O$を作ることができる。
開集合同士の和集合は明らかに開集合である。(境界が自然発生することはないからだ。)
ゆえに$O$も開集合だ。
また位相は、その定義より開基の任意の個数の元の和集合を元としてもつため、
$O$を必ず元として持つ。■

練習問題13: 開基や位相から任意の元を有限な任意個選び、その共通部分を求めると必ず位相の元になることを証明せよ。また、無限個選んだ場合の反例を挙げよ。

→

(証明)
位相は任意の開集合を含んでいるので、
開基や位相の任意の元の共通部分が開集合になることをいえばよい。

さらに開基や位相の任意の元は開集合なので、
開集合の共通部分が開集合になることをいえばよいが、
これは明らかだ。■

無限個選んだ場合の反例は[13]にあるものが使える。

$O_n=\{(x,y)|(x,y)\in\mathbb{R}^2, x^2+y^2<\frac{1}{n}\}$
このような開集合($n$は自然数)を無限個とり、その共通部分をとると、原点の1点となる。
要素を1つしか持たない集合は明らかに閉集合であって、開集合ではない。

練習問題14: 空集合および全体集合が位相の元であるか、議論せよ。ただし、開集合であることと閉集合であることは背反ではないことに注意せよ。

→
空集合は境界を持たない集合なので開集合である。故にその補集合たる全体集合は閉集合である。

しかし、全体集合は開基の元の和集合そのものであるから開集合でもあるはずだ。

したがって、全体集合は開集合でありながら閉集合でもある。

こういうのを「開かつ閉集合」(clopen-set)という。

その補集合である空集合も、開かつ閉集合となる。

どちらも開集合であることには間違いないので、位相の元である。

補足: 開集合であって同時に閉集合でもあるというのは不思議な気もするが、開集合や閉集合そして境界の定義をちゃんと思い出せば、実はそれほどおかしなことでもない。

開集合は自身の境界点をすべて自分以外に押し付けているような集合のことで、閉集合は自身の境界点をすべて自分で持っている集合のことだ。
そして境界点とは、任意の正数$\varepsilon$に対して$\varepsilon$近傍が自身とも、自身の補集合とも共通部分を持つような点のことをいった。
この定義でいえば、空集合に境界はそもそも存在しない。(空集合自身と$\varepsilon$近傍の共通部分は存在しないのだから)
同じように、全体集合にも境界が存在しない。(全体集合の補集合は空集合なので、共通部分を持たせえないのだから)

このように、そもそも境界点が1つも存在しない場合は、その0個の境界点をすべて自分が持っているといっても嘘でないし、すべて自分以外に押し付けたといっても嘘ではない。

身近(?)な例でいうのなら、面白おかしい入社試験を考えてみるとよい。
筆記試験開始直後、問題を見ると白紙なのだ。どうやらミスプリでもなく、全員が全員白紙の試験を受けているようだ。
次に面接を受けたが、面接官がいない。
当然、この企業の試験を受けた花子さんの得点は「0点満点」だ。最高の結果であると同時に最悪の結果だ。当然、太郎君と同得点だ。
しかし、採用・不採用が発表されてみると花子さんは合格、太郎君は不合格だった。
実はこの企業はジェンダー平等に取り組んでいる。アファーマティブアクションの一環として、「同得点の場合、女性を優先して採用する」という措置をとっていた、というオチだ。
_{_{弁解しておくと、この例え話に女性を馬鹿にする意図は一切ない。皮肉を向けられているのは、アファーマティブアクションを肯定する人たちである。}}

このように企業や学校は「0点満点」のテストを受けさせることで好きなように人材を選べるようになる。
それと同じで我々は「境界点が0個」の集合を考えることで、その集合を好きなように開集合または閉集合と考えてよいようになる。

1-4-2. 位相空間とは

位相空間とは、1-4-1節の議論から、「距離」という概念を一切取り除いたものである。言い換えれば、1-4-1節の議論を、「距離」を使わずに展開したとき、それが位相空間である。

ここで注意してほしいのが、「距離を持たない空間」の一種として位相空間があるのではなく、

「距離を必要としない空間」の一種として位相空間があるということだ。

つまり、位相空間が距離を持っていてもかまわないのであるし、また距離空間は必ず位相空間とみることができる。

実際、1-4-1-10節で述べた位相$\mathfrak{O}$を、集合($X$とする)と組み合わせたとき、
位相空間とは$(X,\mathfrak{O})$のことであるからだ。

位相空間では、距離を使わずに議論する必要があるため、「境界の限りなく『近く』」いった議論がそのままではできない。そのため、開集合とか閉集合といった議論も、そのままではできないように思える。

しかし実際には、開集合や閉集合自体は「あらかじめ分かっている」のである。だって、「位相とは任意の開集合を元とする2階集合」のことであるのだから。位相の元である集合であれば開集合だし、位相の元の補集合としてみることができれば閉集合。どちらとしてみることもできれば開かつ閉集合。どちらとしてみることもできなければ、開集合でも閉集合でもないのだ。

1-4-2-1. 位相空間における近傍

「距離」を使わずに近傍を定義するにはどうしたらよいだろう。

わかるのは、「任意の部分集合が開集合、閉集合、開でも閉でもない集合のうち、どれであるか」だけだ。これは位相を見ればわかる。

距離の代わりに集合間の含有関係を用いて「近さ」を定義することができそうだ。つまり、次のようにする。

位相空間の部分集合$A$およびその元$a$をとり、
$a∈O_a⊂A$となる「※集合$O_a$」が存在するとき、$A$を$a$の近傍という。

$O_a$ を挟むことで、近傍の特徴である「少しくらいなら中心からずれても、近傍の範囲内だ」が言えるようになる。

では、その「※集合」は具体的に開集合とするか、閉集合とするか、それとも何でもよいのか議論していこう。

閉集合ではマズい。$O_a={a}$とすることが許されてしまう。
それをしたら$a⊂A$と同じ意味になってしまい
$O_a$を挟んだ意味がなくなってしまう。

この問題は、開集合では起こらない。
したがって、$O_a$ には開集合であることを要求する。

位相空間の部分集合$A$およびその元$a$をとり、
$a∈O_a⊂A$となる開集合$O_a$が存在するとき、$A$を$a$の近傍という。

1-4-2-2. 位相空間における境界

参考:[14]

距離空間において(部分集合$A$の)境界点とは、どんな正数$δ$に対しても、
点$p$の$δ$近傍が「$A$に対してもその補集合に対しても共通部分を持つ」ときの$p$をいった。

位相空間ではこの「$δ$近傍」を考えることができないが、「近傍」を考えることはできる。これをそのまま置き換えれば、位相空間における境界の定義を得る。

位相空間において(部分集合$A$の)境界点とは、点$p$の任意の近傍が「ある$A$に対してもその補集合に対しても共通部分を持つ」ときの$p$のことである。

1-4-2-3. 位相空間における「開集合」と「閉集合」

距離空間では、まず集合と距離があって、距離から境界とか開集合とか閉集合を考えた。

しかし、「位相空間」を考えるときには、まず集合と位相があるわけである。
そして位相とは、開集合を集めた2階集合であった。

つまり、位相空間では開集合が真っ先に与えられ、また閉集合や、それ以外の集合も直ちに決まる。

1-4-2-4. 位相空間における点列の収束とハウスドルフ性

参考:[15][16][17]

位相空間上でも、点列を考えることができる。

点列$a_n$が点$p$へ収束するとは、「$p$のどんな近傍にも$a_n (n_0<n)$が侵入するような$n_0$ が存在すること」である。

実は、点列の収束先は一意でない場合がある。
例えば$(X,{ϕ,X})$という位相空間を考えよう。見ての通り、この空間では開集合は全体集合しかない。(任意の部分集合が必ず閉集合)
近傍は開集合なので、近傍も、全体集合しかない。
したがって、$a_1$ が、すべての点に収束しているといえてしまうのである。

このような事態が起きないための十分条件が、ハウスドルフ性である。

ハウスドルフ性とは、相異なる点を任意に2つとって$p$および$q$とし、$p$のとある近傍を$U(p)$と書くとき、
$U(p)\cap U(q) = \phi$な$U(p)$および$U(q)$が必ず存在することをいう。