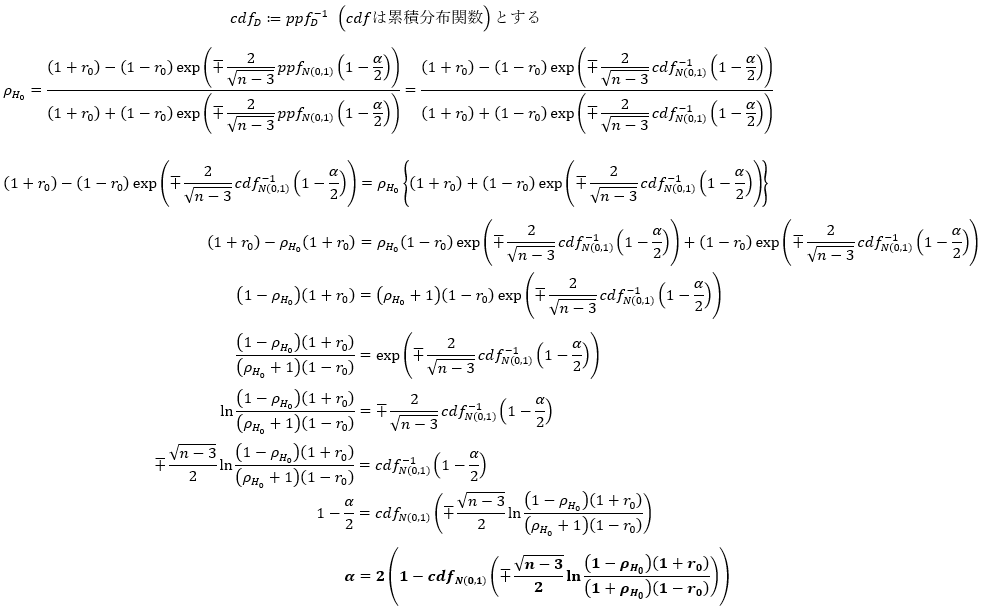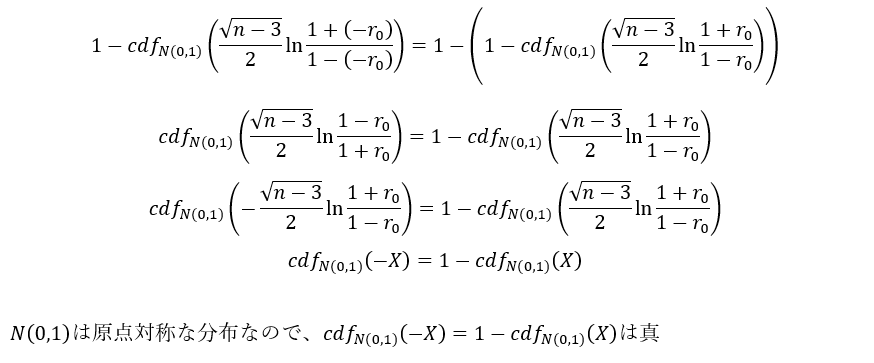編集後記: 長ったらしくなりました。申し訳ございません。統計検定2級受験以上の実力があり、かつお忙しい方は2-4節からお読みいただければ幸いです。
1. 背景
1-1. cos類似度の定義
cos類似度とは「2つのベクトルがどのくらい似ているか」を-1から1の間で定量化する指標です。
高校で習う通り、$\vec{x}\bullet\vec{y}=|\vec{x}||\vec{y}|\cos(\vec{x}と\vec{y}のなす角)$ですので、
$\cos(\vec{x}と\vec{y}のなす角)=\frac{\vec{x}\bullet\vec{y}}{|\vec{x}||\vec{y}|}$です。これをcos類似度と呼んでいるだけです。
1-2. ユークリッド距離にない魅力
cos類似度は「ベクトル間の角度を$\cos$に入れただけのもの」ですので、「ベクトルがどれくらい似ているか」というより
「向きがどれくらい似ているか」なんですよね。だから
①北へ4歩だけ歩くことと、東へ4歩だけ歩くことは全然違う($\cos$類似度は0)
②北へ4歩だけ歩くことと、北へ新幹線でいくことはそっくり($\cos$類似度は1)
ということになります。
「え、ダメじゃん」と思うかもしれませんが、この性質が役立つ場合があるそうです。
例えば、あなたは熱海(JR東日本による東海道線の終点)に住んでいて、これから東京の職場へ向かうとします。
交通手段は東海道線普通列車や東海道新幹線などが考えられます。
さて、あなたは熱海駅で電車に乗った途端、忘れ物に気が付きました。
仕方ないので次の駅で降りて、熱海まで引き返しましょう。
次の駅は何駅でしょうか。
- 普通列車なら、湯河原(熱海から5.5km)です。
熱海から湯河原へ向かうことを①、その逆を②としましょう - 新幹線なら、小田原(熱海から20.7km)です。
熱海から小田原へ向かうことを③、その逆を④としましょう。
ユークリッド距離の考え方では、「①と②は似ている」、「③と④は似ている」と考えることになります。
一方、cos類似度では「①と③は似ている」、「②と④は似ている」と考えることになります。
普通列車や新幹線で移動する「目的」に注目して考える時、ユークリッド距離よりもcos類似度のほうが適しています。
①と③はどちらも職場へ向かう目的での行動ですし、②と④は忘れ物を取りに自宅へ戻る目的での行動です。
このようにcos類似度を使うことで、「普通列車か、それとも新幹線か」のような本質的でない違いを無視できる場合があるのです。
実際の例については、次のような説明があります。
コサイン類似度は、一般的にベクトル間の数値的な大きさを考慮しない場合に使用する測定方法です。
典型的な使用方法は、テキストデータを扱う場合です。ベクトルの大きさや重みを無視して、より単語の類似度を重視したい場合に用います。
例えば、文章Aは「科学」という言葉が文書Bより、頻繁に登場するとします。その場合、文章Aは文章Bより「科学」について言及しているとわかります。しかしながら、比較する文章の長さが揃ってない場合、より長い文章のほうが、たまたま単語が登場する確率が増えてしまいます。
例えば、文章Aの方が長く、「科学」とは関係ないにも関わらず、たまたま「科学」という言葉が多く登場したとします。一方で、短い文章Bが実際に科学の文章だとしたら。このよう場合に、コサイン類似度を使って評価します。
引用元: https://enjoyworks.jp/tech-blog/2242
1-3. 相関係数との関連
2つのベクトル$(\vec{x}, \vec{y})$を「対標本$(X, Y)$における 『中心化された』標本値の対$(x_i-\bar{x}, y_i-\bar{y})$ のリスト」とみる時、
cos類似度は、統計学で出てくる相関係数と同じです。
両者の各因数を定義に従って成分ごとの総和の形で書き直してから比較すると明らかになります。
wsuzume氏の記事の解説がとても分かりやすかったです。
補足: 「ベクトルが一般に中心化された標本のリストと見れるわけないだろ何言ってんの?」という指摘はごもっともです。
中心化された標本のリストに対して総和を求めたとき0にならなければなりませんが、「ベクトルの成分の総和は一般に0」なんてことは確かに言えませんもんね。
故に、「コサイン類似度は相関係数と見れる」ってのは、「そこそこ強い条件付き」の話であって、その条件を無視して言えば「嘘」になります。でも十分高次元なベクトル、すなわち標本サイズの十分大きい標本では、標本平均が母平均に近づくため、母平均で標本平均を代用できるでしょう?だから正直そんなに問題ないかと思います。
1-4. cos類似度にかけられた呪い
さて、cos類似度には問題点があります。それは「ベクトルの次元が高くなるにつれ、0に近い値ばかり出るようになって、1や-1に近い値が出にくくなる」というものです。
1-4-1. 実験
実際に確認してみましょう。
→ 3-1節の結果の表からcos類似度の次元特性も確認できます
1-4-2. 直観的な理解
このような「次元の呪い」は、「角度差を合成すると、より90度に近い角度差の影響がより顕著に表れる」ことによって生じると思います。
このことを直観的に解説させていただきます。
- まず、お手元に鉛筆を用意してもらって、机に真上に立てます。また根本が動かないように右手で押さえておいてください。
- 左手で鉛筆の先を持って、北向きににちょっと(10度くらい)倒してから
- そのまま西向きに倒して地面に寝かせてください(つまり西向きに90度傾けるわけです)。
このとき、鉛筆の向きと「真上」との角度差って、90度ですよね。
このように、「90度でない傾き」と「90度の傾き」を合成すると、合成後の傾きは90度になります。
よって「傾き90度」という次元が1つでも存在すれば、合成後の傾きは90度になるわけです。
ですから、高い次元ほど、『「傾き90度」という次元が最低一つ存在する』確率が上がるので、合成後の傾きは90度になりやすくなるんだろうなと自分は解釈しています。
また、相関係数と絡めて「そりゃ無関係な標本2つの相関係数は標本サイズが十分大きければ0に近づくでしょ、cos類似度でもそれは同じだよね」と考えることもできますね。
2. 理論
第2章ではcos類似度を基に、次のような性質を持つ類似度を定義するための議論を行います。
- 各ベクトルの各成分を$[-1,1]$を一様分布する確率変数とするとき、ベクトル間の類似度は一様分布に近い
- 十分高次元のとき、ベクトルの次元に依存せず、ベクトル間の類似度の分布は一定と見れる。
2-1. 相関係数にかけられた呪い
ベクトルを都合よく解釈することで、cos類似度は相関係数と見れるのでした。
cos類似度は呪われているのでした。
よって、ベクトルを「cos類似度を相関係数とみるための方法①で」解釈するとき、相関係数も呪われているはずです。
ベクトルの次元が高いことを①で解釈すると、「標本の大きさが大きい」ことを意味します。
標本の大きさが大きくなるにつれ、相関係数は0に近づきやすくなり、1や-1に近い値を取りにくくなります。
統計学では、このことを逆の視点から注目します。
「説明変数の種類が標本の大きさに比べて相対的に多くなるにつれ、決定係数(=相関係数の2乗)は1に近づきやすくなる(=相関係数は1や-1に近づきやすくなる)」みたいな感じで。
今回、説明変数の個数は1個(つまり単回帰)で固定ですので、
「標本の大きさが小さくなるにつれ、相関係数は1や-1に近づきやすくなる」と読み替えていいです。
以上、予想通り相関係数もちゃんと呪われていました。
補足: 1-3節の補足にも書いた通り、本当はcos類似度を相関係数とみなすには「成分の平均が0」という強い仮定が必要です。
その辺も関係してくると思うので、「標本の大きさが相対的に小さくなると相関係数が±1に近づく」ことと「次元が高くなるとcos類似度が0に近づく」ことは『同じこと』とまではいえません。
2-2. 次元の呪いに喜ぶ相関係数―自由度調整済み決定係数はcos類似度の次元の呪いを解決しない
僕は「統計学には『自由度調整済み決定係数』があるじゃないか。同じことをコサイン類似度に対してやってみたら次元の呪いをお祓いできるのでは?」とか最初勘違いしていました。
これは大間違いです。決定係数や相関係数の意味をちゃんと考えていませんでした。
cos類似度で問題なのは「次元が高くなると、無作為なベクトル間の類似度が0ばかりになって一様でなくなる」ことでした。
一方、相関係数ってのは、「2データ間の関係性」を示す統計量で、標本サイズが大きければ大きいほど精度が上がります。
ってことは、標本サイズが大きくなればなるほど、「無作為な2データ間」での値は0に近づくし、そうでないと困るのです。
相関係数は、「次元の呪い万々歳」なんです。
したがって、「相関係数をより良くするための工夫」をcos類似度に転用したら、「もっと悪くなる」に決まっているんです。目指している方向が真逆なので。
以上、2-2節は蛇足だったかもしれませんが、同じ勘違いをしている人もいるかもしれませんので、執筆させていただきました。
2-3. 母相関係数の仮説検定
2-3節で扱う「相関係数の区間推定・仮説検定」に関する詳しい解説は、統計検定2級の教科書(東京図書が出してる、公式認定されてるやつ)の5章にあります。
また本節以降は、標本から得られる統計量と母数の区別を明確に理解していることを前提に執筆されていますので、「言ってることややこしいなぁ」と思ったら、統計の教科書などで勉強してください。
Fisherのz変換は、母相関係数を区間推定・仮説検定したいときに利用します。
2-3-1. (やや脱線だけど大事なこと)母数と標本統計量とテロリズム
標本とは、母集団の一部分です。そのため、標本の平均と、母集団の平均は、一致するとは限りません。
平均に限らず、分散、比率、相関係数などについても同じことが言えます。
例えば、警視庁は性犯罪者に関する標本のデータを持っているといえます。ここから「性犯罪者の標本比率は男99.5%である」ということが分かったりします。ここから母比率(性犯罪者全体の男女比)を直ちに知ることはできず、それをやるためには無作為抽出など抽出方法の工夫が必要であることに十分注意してください。
一部の勉強の足りないまたは悪意あるフェミニストやガク者はこの結果に大喜びして「痴漢は男の問題!」とか本気で言っています。
このような言説は攻撃欲や感情に支配され洞察力に欠けた素人による誤りであるか、そうでなければ母集団と標本の区別を故意に曖昧にして、偏見を助長する悪質なデマです。
こういったデマによって偏見が加速することで、女による性犯罪が明るみに出にくくなり、性犯罪者の逮捕が「無作為抽出」からかけ離れていき、母比率と標本比率が乖離していっている可能性すらあります。これが正しければ、彼女たちのしていることは「痴女への間接的加担」と「情報テロリズム」であると非難せざるを得ません。
以上の例のように、母数と標本統計量の混同は、時として偏見や差別を助長し、そのことが理由で母数と標本統計量の乖離を加速するという新手のテロリズムへの入り口となる危険性があるのです。
2-3-2. 母数に対する区間推定と仮説検定
「母数$\theta$を信頼係数$100(1-\alpha)%$で区間推定する」というのは、標本から得られる統計量の実現値$\hat{\theta_0}$に対し
$$f_{\hat{\theta_0}}(\theta) \tilde{} D$$
を根拠として
$$ppf_D\left(\frac{\alpha}{2}\right)
\le f_{\hat{\theta_0}}(\theta) \le ppf_D\left(1-\frac{\alpha}{2}\right) \\
$$
(など)である頻度(※)が$100(1-\alpha)%$である―と考えることを言います。
(「確率$p$を受け取ると『分布$D$において、$x$以下の実現値となる確率は$p$である』といえる『下側$100p$パーセント点$x$』を返す関数」を$x = ppf_D(p)$と書くことにします。$D$は$ppf_D$の既知な確率分布である必要があります。)
※ここで「頻度」と表現し、「確率」といわなかったのは、母数$\theta$は確率変数どころか変数ですらなくて定数であり、「確率的に決まる」と考えるべきではないと考えられているからです。
また「帰無仮説を$H_0: \theta=\theta_{H_0}$として有意水準$100\alpha%$で仮説検定する」というのは、
標本統計量$\hat\theta$の実現値が$\hat\theta_0$の時、
母数$\theta$の具体値が$\theta_{H_0}$であると仮定して、
$$ppf_D\left(\frac{\alpha}{2}\right)
\le f_{\hat\theta_0}(\theta_{H_0}) \le ppf_D\left(1-\frac{\alpha}{2}\right) \\
$$
(など)が偽のとき「帰無仮説$H_0$はたぶん間違っている」と判断するものです。
逆に、この式が真だったからといって「帰無仮説は正しい!」とか言っちゃだめです。「証拠不十分でどちらともいえない」のです。
そういえばstap細胞騒動のとき、「stap細胞があるとは言えない」「ないとは断言できない」という主張をした理研に対してマスコミだったか社会学者だったかが「ハッキリしろ」と批判していましたが、仮説検定にも同様の批判をするつもりなんですかね...(てか理研が行ったのも、「stap細胞はない」を帰無仮説とした仮説検定と見れるのでは?詳細を知らないので断言しませんが。)
一般市民の「知る権利」や「共感」を盾に、科学の根本や真実を捻じ曲げることも厭わない社会カガク独特の気持ち悪さが垣間見えます。
2-3-3. 有意水準とP値
2-3-2節で述べた通り、「有意水準$100\alpha%$で仮説検定する」というのは、
$$ppf_D\left(\frac{\alpha}{2}\right)
\le f_{\hat\theta_0}(\theta_{H_0}) \le ppf_D\left(1-\frac{\alpha}{2}\right) \\
$$
(など)が偽のとき「帰無仮説$H_0$はたぶん間違っている」と判断するものです。
ここで、有意水準とは、「どれくらいレアなことが起これば、自信をもって『$\theta \ne \theta_{H_0}$だ!』といえる」と考えるかのレア度です。
例えば相手がサイコロで6ばかりを出してきたとします。
これが「いかさまサイコロ」であるかを仮説検定するとします。
帰無仮説を「いかさまではない」つまり「6が出る確率は1/6」とします。
有意水準5%であれば、「帰無仮説が正しいとしたら(5%以下の確率でしか)起きない」ことが起きれば、「たぶんいかさまだろ」といえるわけです。例えば今から2回連続して6が出る(確率は1/36)とか。
有意水準1%であれば、「帰無仮説が正しいとしたら(1%以下の確率でしか)起きない」ことが起きれば、「ほぼいかさまだろ」といえるわけです。
例えば今から3回連続して6が出る(確率は1/128)とか。
有意水準が大きければ大きいほど「冤罪」を生みやすいため、有意水準は「危険率」と呼ばれることもあります。
「今から2回連続で6が出る確率」と「単に2回連続で6が出る確率」は全然違います。後者は試行回数に制限が無ければ1に限りなく近づきます。
前者は「1回目が6で、かつ2回目が6である確率」ですが、後者は「『1回目が6で、かつ2回目が6』または『2回目が6で3回目が6』または『3回目が6で4回目が6』または...」と"または"が永遠に続くわけです。
見方を変えると、今から$n$回連続して6が出たときは、有意水準が$6^{-n}$以上であれば「いかさまだろ」といえるし、有意水準がそれ以下なら「いかさまとは言い切れない」と判断することになります。
このように、ある事象を以て帰無仮説を棄却するために必要な危険率(有意水準)のことをP値といいます。
2-3-4. Fisherのz変換
相関係数に対して区間推定・仮説検定を行う過程には、Fisherのz変換という定石があります。
「$x,y$間の相関係数$r$を$z$という変数に変換すると、($x$や$y$の分布が正規分布でない場合ですら)、$z$が正規分布に従う」という性質を利用したものです。ここではそれを紹介します。
但し、執筆途中に「わざわざ$z$なんて記号を利用しない方が完結で分かりやすい」ってことに気が付いてしまったため、本稿では$z$という記号を用いません。ご了承ください。
2-3-4-1. 相関係数の区間推定
「母相関係数$\rho$を信頼係数$100(1-\alpha)%$で区間推定する」には、標本サイズ$n$の標本相関係数$r$に対し
$$f_{r}(\rho) \tilde{} D$$
を根拠として
$$ppf_D\left(\frac{\alpha}{2}\right)
\le f_{r}(\rho) \le ppf_D\left(1-\frac{\alpha}{2}\right) \\
$$
とします。
故に$f_{r}(\rho)$と$D$を手に入れる必要があります。
現在、次のような近似が知られています。
$$f_r(\rho):=\frac{\sqrt{n-3}}{2}\left(\ln{\left(\frac{1+r}{1-r}\frac{1-\rho}{1+\rho}\right)}\right)$$
$$D := N(0,1)$$
(但し$N(0,1)$は標準正規分布を表します。)
一般には次のようになります。
$$ppf_{N(0,1)}\left(\frac{\alpha}{2}\right)\le \frac{\sqrt{n-3}}{2}\left(\ln{\left(\frac{1+r}{1-r}\frac{1-\rho}{1+\rho}\right)}\right) \le ppf_{N(0,1)}\left(1-\frac{\alpha}{2}\right) \\
-ppf_{N(0,1)}\left(1-\frac{\alpha}{2}\right)\le \frac{\sqrt{n-3}}{2}\left(\ln{\left(\frac{1+r}{1-r}\frac{1-\rho}{1+\rho}\right)}\right) \le ppf_{N(0,1)}\left(1-\frac{\alpha}{2}\right) \\
\begin{array}{rl}
\ln{\left(\frac{1+r}{1-r}\frac{1-\rho}{1+\rho}\right)} &= \mp \frac{2}{\sqrt{n-3}}ppf_{N(0,1)}\left(1-\frac{\alpha}{2}\right)\\
\exp\left(\mp \frac{2}{\sqrt{n-3}}ppf_{N(0,1)}\left(1-\frac{\alpha}{2}\right)\right) &= \frac{1+r}{1-r}\frac{1-\rho}{1+\rho}\\
(1-r)(1+\rho)\exp\left(\mp \frac{2}{\sqrt{n-3}}ppf_{N(0,1)}\left(1-\frac{\alpha}{2}\right)\right) &= (1+r)(1-\rho)\\
(1-r)\exp\left(\mp \frac{2}{\sqrt{n-3}}ppf_{N(0,1)}\left(1-\frac{\alpha}{2}\right)\right)+(1-r)\exp\left(\mp \frac{2}{\sqrt{n-3}}ppf_{N(0,1)}\left(1-\frac{\alpha}{2}\right)\right)\rho &= (1+r)-(1+r)\rho
\\
((1-r)\exp\left(\mp \frac{2}{\sqrt{n-3}}ppf_{N(0,1)}\left(1-\frac{\alpha}{2}\right)\right)+(1+r))\rho &= (1+r)-(1-r)\exp(\mp \frac{2}{\sqrt{n-3}}ppf_{N(0,1)}\left(1-\frac{\alpha}{2}\right))
\\
\rho &= \frac{
(1+r)-(1-r)\exp\left(\mp \frac{2}{\sqrt{n-3}}ppf_{N(0,1)}\left(1-\frac{\alpha}{2}\right)\right)
}{
(1+r)+(1-r)\exp\left(\mp \frac{2}{\sqrt{n-3}}ppf_{N(0,1)}\left(1-\frac{\alpha}{2}\right)\right)
}
\end{array}
$$
但し、$\pm$でなくあえて$\mp$と書いているのは、$f$が単調減少する関数であるため、
区間上限を求める際に負号、
区間下限を求める際に正号を採用すべきことを強調するものです。
例えば$n=19, r=0.2$だったとき、信頼係数を95%つまり$\alpha=0.05$とすると
$$\rho = \frac{
(1+r)-(1-r)\exp\left(\mp \frac{2}{\sqrt{n-3}}ppf_{N(0,1)}\left(1-\frac{\alpha}{2}\right)\right)
}{
(1+r)+(1-r)\exp\left(\mp \frac{2}{\sqrt{n-3}}ppf_{N(0,1)}\left(1-\frac{\alpha}{2}\right)\right)
}$$
は
$$\rho = \frac{
1.2-0.8\exp\left( \mp \frac{1}{2}\bullet2\right)
}{
1.2 +0.8 \exp\left(\mp \frac{1}{2}\bullet2\right)
}$$
つまり
$$-0.28 \le\rho\le 0.60 $$
となります。
$ppf_{N(0,1)}(0.975) \approx 1.96\approx2$と
$ppf_{N(0,1)}(1-0.975) \approx -1.96\approx-2$
は正規分布表から求められますが、頻出なのでそのうち覚えてしまうでしょう。
標本サイズが19のとき、標本相関係数が0.2のとき、100回中95回くらいの頻度で、母相関係数は-0.28以上0.60以下の範囲にあるというわけです。
2-3-4-2. 相関係数の仮説検定
標本相関係数が$r_0$であったとします。
母相関係数が$\rho_{H_0}$であるというのを帰無仮説とすると、
不等式
$$\frac{
(1+r_0)-(1-r_0 )\exp\left( \frac{2}{\sqrt{n-3}}ppf_{N(0,1)}\left(1-\frac{\alpha}{2}\right)\right)
}{
(1+r_0)+(1-r_0 )\exp\left( \frac{2}{\sqrt{n-3}}ppf_{N(0,1)}\left(1-\frac{\alpha}{2}\right)\right)
}
\le
\rho_{H_0}
\le
\frac{
(1+r_0)-(1-r_0 )\exp\left(- \frac{2}{\sqrt{n-3}}ppf_{N(0,1)}\left(1-\frac{\alpha}{2}\right)\right)
}{
(1+r_0)+(1-r_0 )\exp\left(-\frac{2}{\sqrt{n-3}}ppf_{N(0,1)}\left(1-\frac{\alpha}{2}\right)\right)
}
$$
が偽のとき、この帰無仮説を棄却できます。
この不等式は2-3-4-1節の不等式に対し$\rho$を$\rho_{H_0}$に、$r$を$r_0$に置き換えたものです。
また$\alpha$を変数とみなし、この不等式の上限あるいは下限と$\rho_{H_0}$を等号で結び直して$\alpha$について解くと、P値を求めることができます。
後はfrom scipy.stat import normすればnorm.cdfが利用できるので、P値$\alpha$を求めることができます。
norm.cdfの速度は、colabで行った実験から、一つずつ計算する場合は8千[回/秒]、配列にまとめて計算する場合は8百万[回/秒]ぐらい(2021/4/4, ハードウェアアクセラレータ=None)くらいです。一方、lambda x:(1+scipy.special.erf(x))/2の速度は12百万[回/秒]ぐらい、lambda x:(1+ (lambda x:((2/(scipy.pi**0.5))*scipy.integrate.quad(lambda t:np.exp(-t**2), 0, x)[0]))(1) )/2の速度は80~100百万[回/秒]くらいでした。
2-3-5. 両側検定と片側検定
2-3-2節では仮説検定について
$$ppf_D\left(\frac{\alpha}{2}\right)
\le f_{\hat\theta_0}(\theta_{H_0}) \le ppf_D\left(1-\frac{\alpha}{2}\right) \\
$$
などが偽のとき「帰無仮説$H_0$はたぶん間違っている」と判断するものです。
といいました。
「など」ってことは、それ以外の場合もあるわけです。
$$ppf_D\left(\frac{\alpha}{2}\right)
\le f_{\hat\theta_0}(\theta_{H_0}) \le ppf_D\left(1-\frac{\alpha}{2}\right)\\
$$
は、仮説検定の一種である「両側検定」に用いられるものです。
両側検定でない仮説検定には「片側検定」があり、それは次のいずれかになります。
- $$f_{\hat\theta_0}(\theta_{H_0}) \le ppf_D\left(1-\alpha\right) $$
偽のとき、帰無仮説を棄却します。 - $$ppf_D\left(\alpha\right) \le f_{\hat\theta_0}(\theta_{H_0})$$
偽のとき、帰無仮説を棄却します。
相関係数に対する片側検定の場合、
$$\frac{
(1+r_0)-(1-r_0 )\exp\left( \frac{2}{\sqrt{n-3}}ppf_{N(0,1)}\left(1-\alpha\right)\right)
}{
(1+r_0)+(1-r_0 )\exp\left( \frac{2}{\sqrt{n-3}}ppf_{N(0,1)}\left(1-\alpha\right)\right)
}
\le
\rho_{H_0}$$
あるいは
$$
\rho_{H_0}
\le
\frac{
(1+r_0)-(1-r_0 )\exp\left(- \frac{2}{\sqrt{n-3}}ppf_{N(0,1)}\left(1-\alpha\right)\right)
}{
(1+r_0)+(1-r_0 )\exp\left(- \frac{2}{\sqrt{n-3}}ppf_{N(0,1)}\left(1-\alpha\right)\right)
}
$$
が偽のとき、帰無仮説を棄却します。
2-4. 直交描度―P値を用いた新しいベクトル類似度の提案
2-4-1. 直交非尤度
2-3-3節でも述べた通り、「母相関係数を$\rho_{H_0}$と仮定したときの標本相関係数のP値」というのは「母相関係数が$\rho_{H_0}$でないと決めつけることがどれだけ危険(冤罪リスクを生む)か」を表しています。
言い換えれば、これは「母相関係数が$\rho_{H_0}$だったとしたら、今得られた標本相関係数はどのくらいの頻度で得られるのだろう」という量です。つまり、値が大きければ大きいほど「母相関係数が本当に$\rho_{H_0}$である」ことの尤度が高くなるわけですし、値が小さければ小さいほど「母相関係数の絶対値は本当は$\rho_{H_0}$ではない」ことの尤度(みたいの)が高くなります。
さて、「母相関係数を0と仮定したときの標本相関係数のP値」つまり「母相関係数が0だったとしたら、今得られた標本相関係数はどのくらいの頻度で得られるのだろう」という量※は、ベクトルの言葉で言い換えるとだいたい次のような意味になります。(「だいたい」とわざわざ言っているのは、中心化を無視していることの強調です)
類似度を測ろうとしている2つの$n$次元ベクトル$\vec{x}, \vec{y}$を、「実は2つの無限次元ベクトル(『母ベクトル』と呼ぼう)$\vec{X}, \vec{Y}$から互いに同じ次元を$n$つだけ無作為にとってきて、順番を入れ替えずにそのまま並べて新たに作った『部分ベクトル』的なベクトルなんだ」と考えよう。
$\vec{X}\bullet\vec{Y}/|\vec{X}||\vec{Y}|=0$だった(つまり母ベクトルが直交している)としたら、既に得られている$\vec{x}\bullet\vec{y}/|\vec{x}||\vec{y}|$はどれくらいの頻度で得られるのだろう。
そこで、※を「(母ベクトル)(両側)直交(擬)尤度」と呼ぶことにしましょう。(「擬」尤度とわざわざ言っているのは(ry
直交尤度が大きいほど、母ベクトルのcos類似度(≒母相関係数)の絶対値は小さそうなのです。
これだと直感と逆になっていてややこしいので補正しましょう。
P値の最大値は1ですから、「$1-\alpha=1-P値$」が大きければ大きいほど、「母相関係数(あるいはその絶対値)は大きかろう」といえることになるわけです。これを「直交非尤度」とでも呼びましょう。
2-4-2. 両側P値と片側P値
2-4-1節でいったP値は、両側検定を行うか、それとも片側検定(上側or下側)を行うかによって3通りが考えられます。
両側検定によるP値から求められる直交非尤度は、「母相関係数の絶対値がどれだけ大きそうか」を表します。
片側検定で、「母相関係数は0以上」を前提とする場合、直交非尤度は「母相関係数がどれだけ大きそうか」を表します。
片側検定で、「母相関係数は0以下」を前提とする場合、直交非尤度は「母相関係数の符号反転がどれだけ大きそうか」を表します。
以上のようにまとめると、両側P値と片側P値の長所短所が見えてきます。
両側P値を用いると、母相関係数の正負が分からなくてもP値を求められますが、その代わりに母相関係数の正負をP値から求めることができません。両側P値を用いて定義する新しい類似度「両側直交描度」については2-4-3節で説明します。
片側P値では、母相関係数の正負が想定と逆であった場合にP値がどうなるか分かりません。片側P値を用いて定義する新しい類似度「片側直交描度」については2-4-4節で説明します。
2-4-3. 両側直交描度
両側検定による直行非尤度は標本相関係数の関数であり、「母相関係数の絶対値がどれだけ大きそうか」を表します。
母相関係数の符号の推定には、標本相関係数の符号をそのまま採用しましょう。
以上のような定義に従う量を「両側直交描度」と呼ぶことにします。
(理論上、両側直交描度では、その絶対値が小さければ小さいほど、その符号と母相関係数の本来の符号が一致しない可能性が大きくなります。)
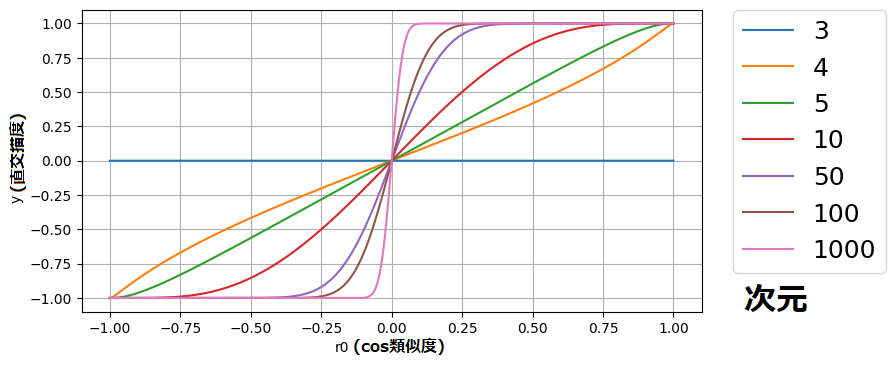
図2-4-3-1は、両側直交描度の、$r_0$及び標本サイズ特性です。ベクトルの言葉で言えば、cos類似度及び次元特性です。
横軸、縦軸共に区間[-1,1]内を動き、単調増加であって、また標本サイズが大きくなればなるほど両側直交描度は±1に極端に近い値を取る傾向があります。換言すれば、$r_0=0$付近での傾きが急です。
図2-4-3-1および図2-4-4-1はこちらのcolabで得られました。
2-4-4. 片側直交描度
「母相関係数は0以上」を前提とする場合の片側検定による直行非尤度($1-P値$)は標本相関係数の関数であり、「母相関係数がどれだけ大きそうか」を表します。
標本相関係数が0のとき、直行非尤度は0.5となります。
標本相関係数が1に近いとき、直行非尤度は1に近づきます。
標本相関係数が-1に近いとき、直行非尤度は0に近づきます(※)。
※について、母相関係数が0以上を前提としているのに標本相関係数が負となることについて違和感を覚える方もいるかもしれませんが、母相関係数が正であることは、標本相関係数が負になることを完全に否定するわけではないです。例えば母相関係数が0.1で、母相関係数と標本相関係数の間に最大0.2の誤差が見込まれる場合、標本相関係数は-0.1以上0.3以下の値に決まります。
そこで、「母相関係数は0以上」を前提とする直行非尤度から0.5を引いて2倍した値を「上側直交描度」と定義します。すると
標本相関係数が0のとき、直交非尤度は0.5、上側直交描度は0となります。
標本相関係数が1に近いとき、直交非尤度は1、上側直交描度は1に近づきます。
標本相関係数が-1に近いとき、直交非尤度は0、上側直交描度は-1に近づきます。
また、「母相関係数は0以下」を前提とする「下側直交描度」を定義しても、符号を入れ替えるだけで全く同じ結論を得ます。
そのため上側直交描度と下側直交描度は区別する必要がありません。
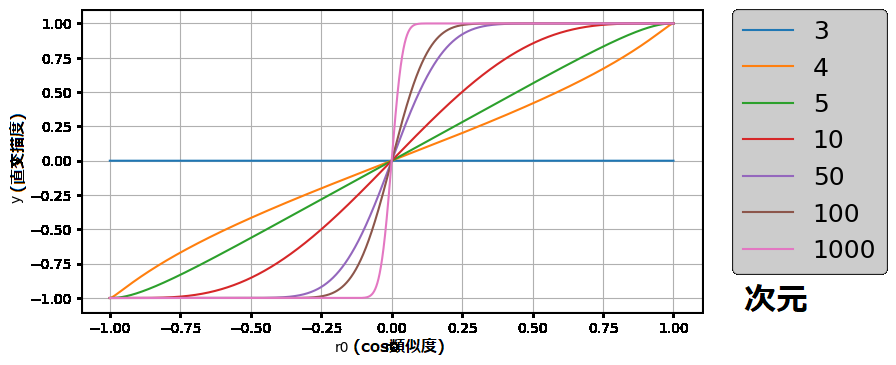
図2-4-3-1および図2-4-4-1はこちらのcolabで得られました。
2-4-5. 両側直交描度と片側直交描度の同等性
図2-4-3-1(両側直交描度)と図2-4-4-1(片側直交描度)を比較してみると、特性が酷似していることがお分かりいただけるかと思います。
これは、両側直交描度と片側直交描度が等価だからです。
以下、説明を簡単にするために$f_{\mp }(r_0):=\left(1- cdf_{N(0,1)}\left(\mp \frac{\sqrt{n-3} }{2} \ln \frac{1+r_0}{1-r_0} \right)\right)$とさせていただきます。
両側直交描度は${\rm sgn}(r_0)\times(1-2f_{+}(|r_0|))$により計算されます。(直交非尤度$1-2f_{+}(|r_0|)$に、$r_0$の符号に合わせて$\pm 1$をかけるというわけです)
一方、片側直交描度は$2((1-f_{+}(r_0))-0.5)$つまり$1-2f_{+}(r_0) $と計算されます。(直交非尤度$1-f_{+}(r_0)$から0.5を引き、2倍します)
両側直交描度と片側直交描度の両者を比較してみましょう。
両者は$r_0>0$のとき、明らかに等しいです。
$r_0=0 $のとき、$f_{+}(0)=1/2$なら両者は等しいですが、$f_{+}$の定義式を使って確認してみると、$f_{+}(0)=1-cdf_{N(0,1)}(0)=1/2$なので、やはり両者は等しいです。
$r_0<0$のとき、$-(1-2f_{+}(-r_0)) = 1-2f_{+}(r_0) $つまり$f_{+}(-r_0)=1-f_{+}(r_0)$なら両者は等しいですが、$f_{+}$の定義式を使って確認してみると、
より、やはり両者は等しいのです。
以上、両側直交描度と片側直交描度は常に同等であることが証明されました。
そのため今後は両者を呼び分けることはせず、単に「直交描度」と呼ぶことにします。
3. 実験
3-1. cos類似度と直交描度の比較(両側描度)
試行回数 = 70000×(次元), 階級数(binの数)=50, 次元=3,4,5,10,50,100について、
各成分が区間[-1,1]を一様分布するような2つのベクトルの組を無作為に作り、cos類似度と直交描度を求める試行を繰り返し、
cos類似度や直交描度の分布を実測してみました。
こちらのcolabで実験を行いました。この記事では結果だけお伝えします。
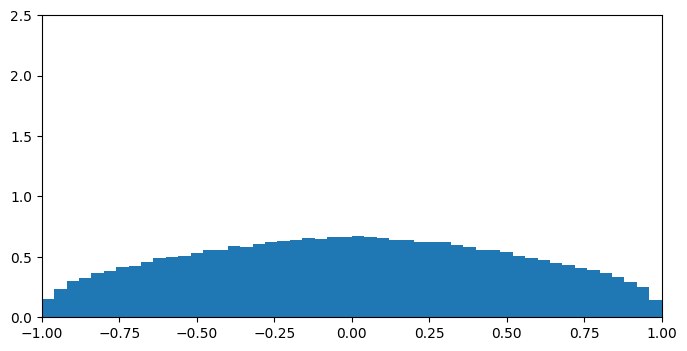
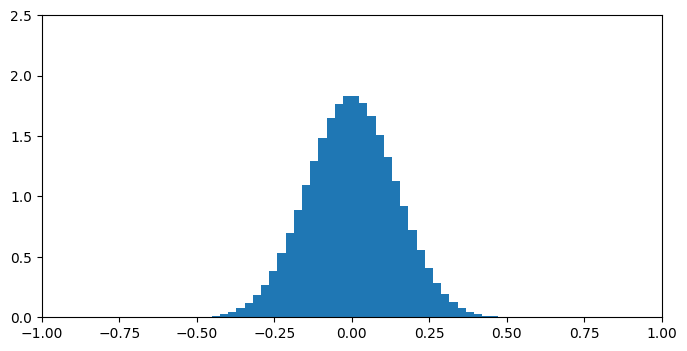
表3.1.1 実験結果(縦軸は密度。つまりヒストグラム全体の面積が1となるよう調整)
| 次元 | 直交描度 | cos類似度 |
|---|---|---|
| 3 |
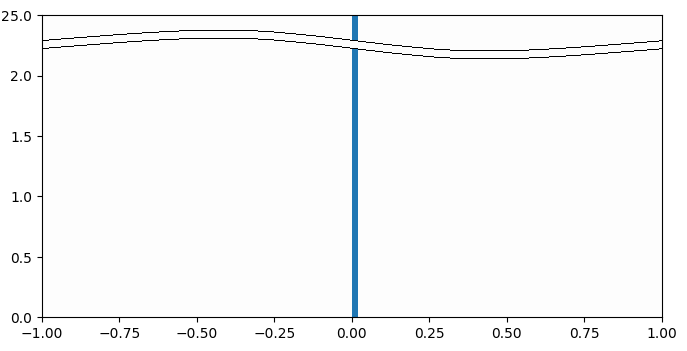 式の因数に√(次元-3)が含まれることにより、3次元では直交描度は常に0となる。 式の因数に√(次元-3)が含まれることにより、3次元では直交描度は常に0となる。 |
 |
| 4 |  |
 |
| 5 |  |
 |
| 10 |  |
 |
| 50 |  |
 |
| 100 |  |
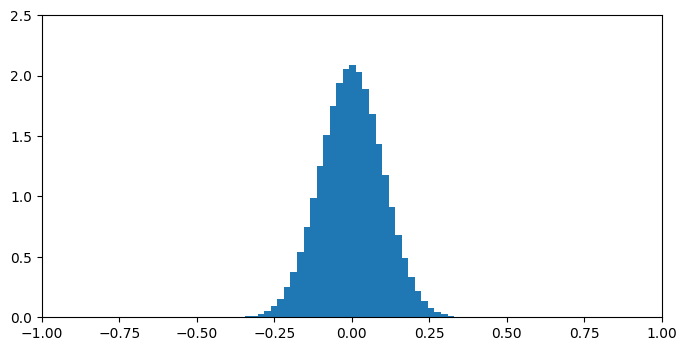 |
直交描度では低次元では一点に集中し全体に一様分布しないものの、50次元を過ぎたあたりから定義域[-1,1]をほぼ一様に分布していることが分かります。こうなれば、それ以降どんなに次元が上がっても分布が大きく変化することはありません(たぶん)。
一方、cos類似度では低次元で一様分布に近いですが、高次元になるにつれ分布が一点に集中してしまいます。
直交描度にて低次元で非一様性がみられる原因として考えられる原因は、(頭の悪い筆者ですら思いついたものは)2つあります。
- ①で中心化を無視したツケが回ってきた
- 相関係数の分布はあくまでも近似式。標本サイズが小さすぎれば崩壊する
4.応用
現在求職中でして、ハロワの求人票見るので疲れてしまって書く気力が湧きません。ごめんなさい。精神安定を図りつつ、また今度気が向いたら書くかもしれません。