ABテストを実施していない観察データを用いた因果推論では、傾向スコアを用いて重み付けすること(IPW)が一般的です。
いざ手元の観察データで分析手法を当ててみてもうまくいかないことが多くあり、原因のひとつとしてIPWによる過大・過小調整が挙げられます。
今回は、処置群と対照群のサンプル比を変えた複数のデータセットにIPWを適用し、それぞれ適切に調整できているかを確認します。
傾向スコア
- 傾向スコア: 共変量を考慮し、処置を受ける確率
- 例: 血圧を下げる薬の処方は、年齢・性別・基礎疾患の有無・生活習慣などの影響を加味する。塩分の高い食事が多い人ほど、傾向スコアが高くなる。
- IPW: 傾向スコアの逆数を使って重み付けする
- メリット: 処置群と対照群のバランスを調整できる。バイアスの除去。欠損データの補完。
- デメリット: 一部のサンプルが過大・過小に調整される。(傾向スコア0.001のサンプルの場合、逆数をかけると1000倍される)
- 詳細は、以下の記事がわかりやすいです。
使用データ
『岩波データサイエンス Vol.3』のデータセットを使用します。

出所 『加藤・星野 サポートページ(岩波データサイエンスVol.3 特集 因果推論)』
- 上図に加えて、以下の変数も含まれます。
-
cm_dummy: CMの視聴有無 -
gamesecond: ゲーム利用時間 -
gamecount: ゲーム利用回数 -
gamedummy: ゲームの利用有無
-
- これらの変数を「アウトカム、処置変数、共変量」にわけて考えます。
- アウトカム: 最終的に確認したい効果
- 処置変数: 処置の割り当て
- 共変量: 処置以外でアウトカムに影響を及ぼしうる変数
- 今回は以下のように整理しました。
- アウトカム:
gamesecond - 処置変数:
cm_dummy - 共変量:
TVwatch_day,age,sex,marry_dummy,child_dummy,inc,pmoney,job_dummy1,job_dummy2,job_dummy3,job_dummy4,job_dummy5,job_dummy6,job_dummy7,fam_str_dummy1,fam_str_dummy2,fam_str_dummy3,fam_str_dummy4,area_kanto,area_tokai,area_keihanshin
- アウトカム:
検証
- 課題
- データセットのサンプル比が偏っていると、その偏りが傾向スコアに反映される。偏った傾向スコアで調整しようとしてもバイアスが十分に取り除けない。
- 検証観点
- 傾向スコアに妥当性があるか。
- 評価方法
- 処置群と対照群の共変量の標準化平均差がIPWによって小さくなっているか。(±0.1の範囲が理想)
- 想定ケース
- 自社でとあるマーケティング施策を実施し、その効果を推定したい。しかし、とある施策のターゲット群に対してほとんどアプローチしている(処置群)。一方で、施策の予算上、一部の優先度が低い人たちにはアプローチしなかった(対照群)。本当にこの施策に効果あったのかを検証したいと相談を受けた。
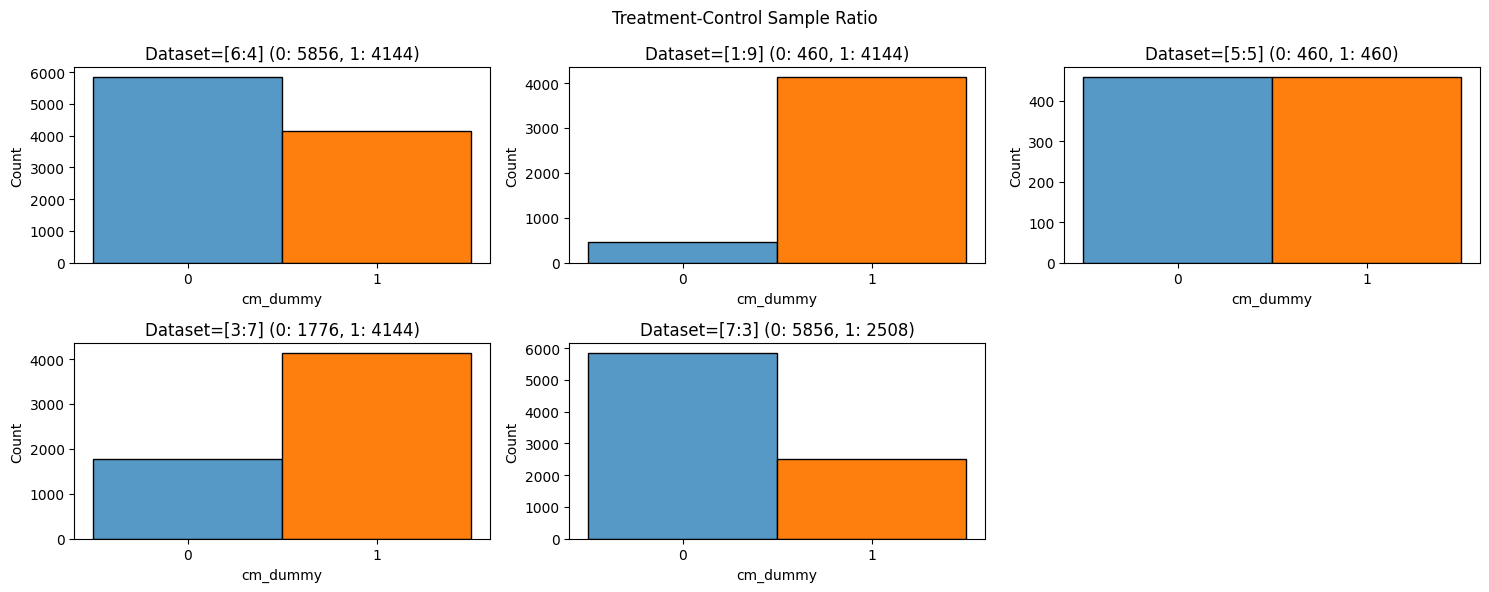
1. サンプル比の異なるデータセット作成
- 上記の使用データからランダムにサンプリングし、処置群と対照群でサンプル比が異なるデータセットを作成します。
| # | データセット | 対照群{cm_dummy:0} | 処置群{cm_dummy:1} | ||
|---|---|---|---|---|---|
| 1 | オリジナル | 60% | 5859人 | 40% | 4144人 |
| 2 | 不均衡 | 10% | 460人 | 90% | 4144人 |
| 3 | バランス | 50% | 460人 | 50% | 460人 |
| 4 | やや偏り | 30% | 1776人 | 70% | 4166人 |
| 5 | やや偏り | 70% | 5856人 | 30% | 2506人 |
- それぞれのデータセットは、以下の状況を想定して、データが収集されたものとします。
- オリジナルのデータセットは、
cm_dummyが4対6くらいで、ある程度ABテストが計画されて施策が打たれた - 不均衡なデータセットは、
cm_dummyが1対9で、施策のターゲットのほぼ全数に向けて施策を打った - バランスの取れたデータセットは、
cm_dummyが5:5で、不均衡なデータセットからサンプリングした - やや処置群に偏ったデータセットは、
cm_dummyが3:7で、オリジナルのデータセットから対照群のみサンプリングした - やや対照群に偏ったデータセットは、
cm_dummyが7:3で、オリジナルのデータセットから対照群のみサンプリングした
- オリジナルのデータセットは、
import numpy as np
import pandas as pd
SEED = 42
# 1. オリジナル[6:4]
df_original = pd.read_csv('https://github.com/iwanami-datascience/vol3/raw/master/kato%26hoshino/q_data_x.csv')
# 2. 不均衡[1:9]
n_sample = df_original['cm_dummy'].value_counts()[1] // 9
df_imbalanced = pd.concat(
[df_original[df_original['cm_dummy'] == 1], df_original[df_original['cm_dummy'] == 0].sample(n=n_sample, random_state=SEED)]
).reset_index(drop=True)
# 3. バランス[5:5]
n_sample = df_imbalanced['cm_dummy'].value_counts()[0]
df_balanced = pd.concat(
[df_imbalanced[df_imbalanced['cm_dummy'] == 0], df_imbalanced[df_imbalanced['cm_dummy'] == 1].sample(n=n_control, random_state=SEED)]
).reset_index(drop=True)
# 4. やや偏り[3:7]
n_sample = df_original['cm_dummy'].value_counts()[1] // 7 * 3
df_imbalanced_3_7 = pd.concat(
[df_original[df_original['cm_dummy'] == 0].sample(n=n_sample, random_state=SEED), df_original[df_original['cm_dummy'] == 1]]
).reset_index(drop=True)
# 5. やや偏り[7:3]
n_sample = df_original['cm_dummy'].value_counts()[0] // 7 * 3
df_imbalanced_7_3 = pd.concat(
[df_original[df_original['cm_dummy'] == 0], df_original[df_original['cm_dummy'] == 1].sample(n=n_sample, random_state=SEED)]
).reset_index(drop=True)
2. 傾向スコアの算出
- 一般的に傾向スコアは、ロジスティック回帰を用いて求めます。
- 傾向スコアモデルの良し悪しは、AUCが0.8以上を基準に判断することが多いです。
- 目的変数は
cm_dummy、モデルに含める変数は使用データに記載の共変量すべてです。- モデルに含める変数選択も重要となってきますが、今回はどのデータセットでも同じ変数を含めます。
import statsmodels.api as sm
def get_propensity_score(df, treatment_col, covariate_cols):
X = df[covariate_cols]
T = df[treatment_col]
exog = sm.add_constant(X)
logit_model = sm.Logit(endog=T, exog=exog).fit()
return logit_model.predict(exog)
treatment_col = 'cm_dummy'
covariate_cols = [
'TVwatch_day', 'age', 'sex', 'marry_dummy', 'child_dummy', 'inc', 'pmoney',
'area_kanto', 'area_tokai', 'area_keihanshin',
'job_dummy1', 'job_dummy2', 'job_dummy3', 'job_dummy4', 'job_dummy5', 'job_dummy6', 'job_dummy7',
'fam_str_dummy1', 'fam_str_dummy2', 'fam_str_dummy3', 'fam_str_dummy4'
]
ps = get_propensity_score(df, treatment_col, covariate_cols)
- どのデータセットでもAUCがほぼ0.8であることから、傾向スコアモデル自体に問題はないと考えられます。
- 傾向スコアの分布を見てみると、傾向スコアの偏りがよくわかります。
3. 共変量のバランス
- 求めた傾向スコアによってバイアスが取り除けるかを、共変量のバランスを調整することによって、傾向スコアの妥当性を確認します。
- 処置群と対照群の共変量のバランスは、標準化平均差(SMD)を使って、評価します。一般的に、±0.1以下だと2群間でバランスが取れていると言えます。
- $SMD = \frac{{\text{処置群の平均値} - \text{対照群の平均値}}}{{\text{プールした標準偏差}}}$
- 詳細は31-3. 効果量2 - 統計WEBを参照。Hedgeのgを使用。
def calc_smd(X1, X0):
N1 = len(X1)
N0 = len(X0)
s_pool = ((N1-1) * np.var(X1) + (N0-1) * np.var(X0)) / (N1 + N0 - 2)
return (np.mean(X1) - np.mean(X0)) / np.sqrt(s_pool)
def adjust_covariate_by_ipw(df, treatment_col, covariate_cols, ps):
X = df[covariate_cols]
T = df[treatment_col]
X0 = X[T==0]
X1 = X[T==1]
ps0 = ps[T==0]
X1_0 = X0 * ps0 / (1 - ps0) # 反実仮想: 処置群が処置を受けなかった場合の共変量
smd_before = calc_smd(X1, X0)
smd_after = calc_smd(X1, X1_0)
return smd_before, smd_after
smd_before, smd_after = adjust_covariate_by_ipw(df, treatment_col, covariate_cols, ps)
- オリジナルのデータセットは、ほとんどの共変量でSMDが±0.1の範囲に調整されています。
- 何も調整していない場合、
area_keihanshin,TVwatch_dayは処置群と対照群とでバランスが取れておらず、その後の推定にバイアスが生じる可能性があります。
- 不均衡なデータセットは、どの共変量も調整後のほうが、SMDが大きくなってしまいました。
- 各共変量は期待していた調整よりも、傾向スコアが小さいサンプルは過大に、大きいサンプルは過小になり、IPWのデメリットが現れていると言えます。
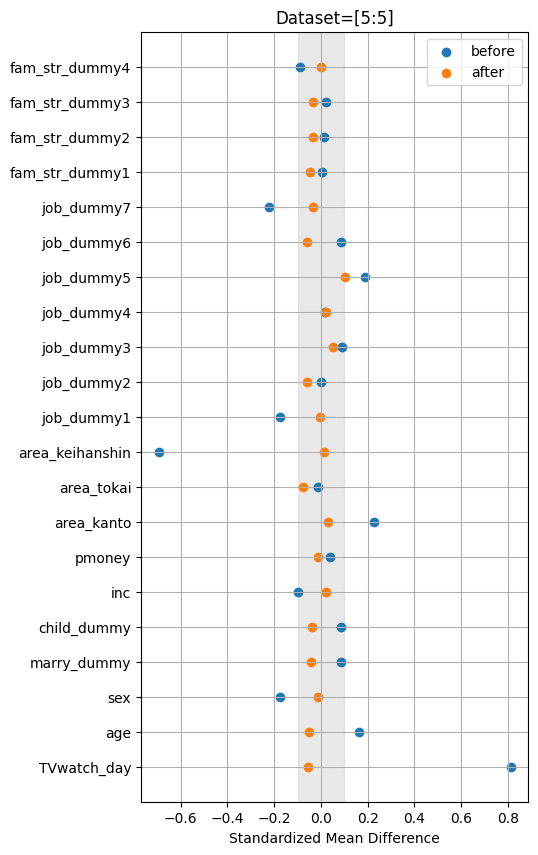
- バランスの取れたデータセットは、
job_dummy5がわずかにSMD0.1を超えているくらいで、すべての共変量のバランスが取れていると言えます。 - 調整前のSMDを、オリジナルのデータセットと比較してみても、大幅に異なる共変量はみられないため、サンプリング自体も悪くなさそうです。
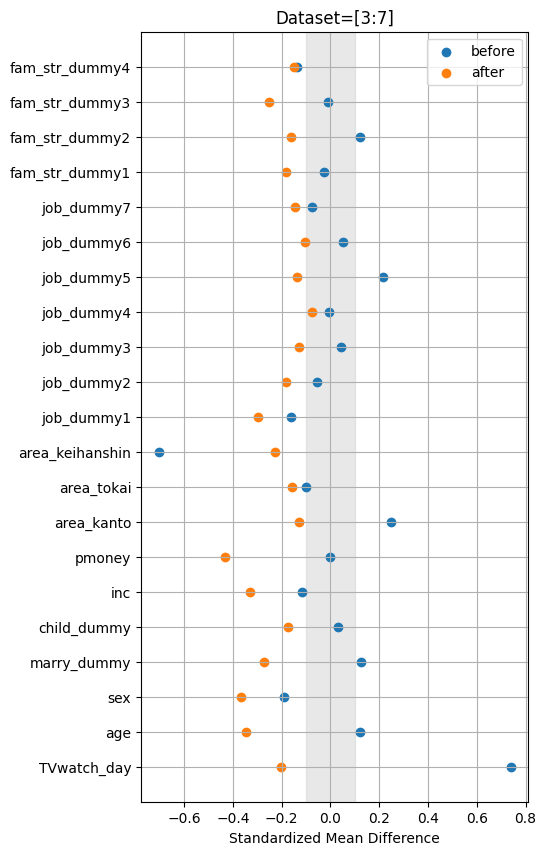
- やや偏ったデータセットは、処置群もしくは対照群のサンプルが少ない方に引っ張られ、SMDが大きくなっています。
| # | データセット | 対照群{cm_dummy:0} | 処置群{cm_dummy:1} | 調整前 | 調整後 | (調整後-調整前) |
|---|---|---|---|---|---|---|
| 1 | オリジナル | 60% | 40% | 3.124 | 1.259 | -1.864 |
| 2 | 不均衡 | 10% | 90% | 3.340 | 10.039 | 6.698 |
| 3 | バランス | 50% | 50% | 3.302 | 0.799 | -2.502 |
| 4 | やや偏り | 30% | 70% | 3.286 | 4.447 | 1.161 |
| 5 | やや偏り | 70% | 30% | 3.199 | 4.410 | 1.210 |
- 調整前と調整後の数値は、各共変量のSMDに絶対値を取り合計したもの。
- 対照群と処置群のサンプル比が6対4と5対5のデータセットでは、2群間のバランスを改善できています。
4. (効果の推定)
- 参考程度に、各データセットから推定した効果を記載します。cmの視聴有無が
gamesecondにどのくらい影響があったかです。 - サンプリングによって、それぞれのサンプルの特徴が変わっているため、データセット間での効果の比較自体に意味はありません。
- 施策とその効果を解釈する際にはターゲット母集団の定義と照らし合わせながら、効果を確認する必要があります。
- ナイーブ: 処置群の平均と対照群の平均との差
- $Naive = E[Y_1 | T=1] - E[Y_0 | T=0]$
- セレクションバイアスが生じている場合、正確に施策の効果が推定できない
- ATT; Average Treatment Effect on the Tread : 処置群における平均処置効果
- $ATT = E[Y_1 - Y_0 | T=1]$
- 処置群が処置を受けていない時のデータは現実には存在しないので、上の式における
Y_0は処置群の実測値に傾向スコア(T=0のとき)の逆数をかけることで求まる。
- ナイーブ: 処置群の平均と対照群の平均との差
| # | データセット | 対照群{cm_dummy:0} | 処置群{cm_dummy:1} | ナイーブ(調整前) | ATT(調整後) | 標準偏差 |
|---|---|---|---|---|---|---|
| 1 | オリジナル | 60% | 40% | -627 | 434 | 362 |
| 2 | 不均衡 | 10% | 90% | -1493 | 1214 | 311 |
| 3 | バランス | 50% | 50% | -1922 | 391 | 972 |
| 4 | やや偏り | 30% | 70% | -395 | 709 | 708 |
| 5 | やや偏り | 70% | 30% | -740 | 109 | 911 |
- ナイーブな手法で効果を推定しようとすると、CMを見ることによってゲームの利用時間が減少すると出ます。
- cmを普段から見る層(高齢者層)はそこまでゲームをしない、普段からゲームをやっている層(若年層)などのバランスが取れていないと考えられます。
まとめ
- 傾向スコアで共変量のバランスを調整する際には、処置群と対照群のサンプル比に注意する。
- 2群間の場合、サンプル比は1:1が理想であり、そこからかけ離れると妥当性のある傾向スコアが求められないことがある。
- 傾向スコアの妥当性は、標準化平均差によって共変量のバランスを確認する。
- 傾向スコアで調整して求めた処置効果は、どんな母集団を代表しているのかを意識した上で分析する。
参考文献
- 加藤, 星野. "加藤・星野 サポートページ(岩波データサイエンスVol.3 特集 因果推論)". 岩波データサイエンス
- Yohei Hashimoto. "Theory and practice of propensity score analysis". Annals of Clinical Epidemiology, 2022, Volume 4, Issue 4, Pages 101-109
- Peter C. Austin, Elizabeth A. Stuart. "Moving towards best practice when using inverse probability of treatment weighting (IPTW) using the propensity score to estimate causal treatment effects in observational studies". National Library of Medicine, 2015, Dec, 10; 34(28): 3661–3679.
- 畠山真吾. "数式一切なし、臨床医のための実践的な臨床統計講座". 弘前大学大学院医学研究科, 2022"