AIで為替自動取引アルゴリズムの開発
今回は、ランダムフォレストでドル円のレートが上がるか、下がるか、そのままかを予測するクラス分類モデルを構築しました。
最初に方針を立てる
回帰モデルor分類モデルの選択→分類モデルにしよう
まず、なぜ回帰モデル(つまりレートをドンピシャで推測するモデル)ではなく、クラス分類モデル(つまりレートが上がるか、下がるか、そのままかの三値分類)を選択したのか。
理由はいくつかあります。
・分類モデルの評価は回帰モデルに比べて直観的(今回は混同行列を算出しました。)
・実際にfxで人間が行う動作って(買う、売る、何もしない)の三つだけだしクラス分類でよくない?
・ランダムフォレストちょうど実装したかったんだよね
という理由からクラス分類予測を選択しました。
(後から考えると、通過売買において取引量も大事になってきます。取引量を決める際に具体的なレートは大切になってくるので、ピンポイントでレートを予測できる回帰モデルの方がよかったかな〜なんて思ってます。また今度やってみます。)
特徴量どうしよう→テクニカル指標使おう
fxのレート予測モデルを立てる上で特徴量どうしよう、、、ってなりますよね。
じゃあ実際に人間が何を使ってドル円を売買しているのかを考えれば特徴量も浮かんできます。
人間はfxで取引する際に行う分析は大きく分けて、テクニカル分析とファンダメンタル分析の二つです。
テクニカル分析っていうのはいわゆるチャートを見て値動きを予想することです。
一方ファンダメンタル分析っていうのはニュースとか世界情勢から値動きを予想することです。
今回は機械学習の特徴量として取り込みやすい、テクニカル分析を用います。
なぜ取り込みやすいかというとテクニカル分析は数字だけを扱いプログラム化が簡単だからです。
一方ファンダメンタルも取り込もうと思えばできるのですが(テキストマイニングとかすると)、大変でありそもそもファンダメンタルは長期目線での売買に使われることが多いので使用は見送ります。
データセット
方針も決まってきたのでデータセットを探そう。
今回は、investing.com の過去20年分の日足データを使いました。
大体、250日(fx取引は平日のみ)×20年〜5000個のデータを取れます。
実装!!!
1. レート情報が入ったcsvファイル読み込み
import pandas as pd
df = pd.read_csv("USD_JPY.csv")
2. 特徴量(説明変数)の作成
前述の通り、今回は特徴量としてテクニカル分析の数値を用います。
具体的に今回用いたのは、SMA5,SMA20,RSI14,MACD,Bollinger-bands(2σ)の5つです。
各テクニカル指標の詳しい特徴に関してはググってください。
ただし特徴量として用いるテクニカル指標選びの際に気をつけたいのは、いくら統計分析ではなく機械学習だからといってもマルチコ(多重共線性)は極力避けたいので、できるかぎりお互いに相関性のないテクニカル指標を選んでください。
テクニカル指標の計算は、超絶便利なtalibというライブラリを使いましょう。一発でテクニカル指標を算出してくれます。
ここで、RSIとMACDに関してはテクニカルの数値そのままを使っているのですが、SMAとボリンジャーバンド の値はそうはいきません。(例えばSMAの値が105だったとしても、そのままだとこの105という数値が高いのか低いのかわからないので特徴量としては適していません。)
そこで、SMAとボリンジャーバンドの値に関してはcloseの値で割ってあげることで、相対的で比較可能な値に変換してから特徴量として用いることにします。
この部分に関しては、やり方は他にもたくさんあると思うので各自がいいと思うやり方を試してみてください!
import talib as ta
import numpy as np
# 以降全ての計算でレート終値を使う
close = np.array(df["終値"])
# 特徴量を入れるための空のdataframeを作成
df_feature = pd.DataFrame(index=range(len(df)),columns=["SMA5/current", "SMA20/current","RSI","MACD","BBANDS+2σ","BBANDS-2σ"])
# 以下、talibを用いてテクニカル指標(今回の学習で用いる特徴量)を算出しdf_feature入れる
# 単純移動平均は、単純移動平均値とその日の終値の比を特徴量として用いる
df_feature["SMA5/current"]= ta.SMA(close, timeperiod=5) / close
df_feature["SMA20/current"]= ta.SMA(close, timeperiod=20) / close
# RSI
df_feature["RSI"] = ta.RSI(close, timeperiod=14)
# MACD
df_feature["MACD"], _ , _= ta.MACD(close, fastperiod=12, slowperiod=26, signalperiod=9)
# ボリンジャーバンド
upper, middle, lower = ta.BBANDS(close, timeperiod=20, nbdevup=3, nbdevdn=3)
df_feature["BBANDS+2σ"] = upper / close
df_feature["BBANDS-2σ"] = lower / close
3. 教師データ(目的変数)の作成
前述した通り、今回のモデルの教師データは[上がる、下がる、値は(ほぼ)変わらない]の三値です。
そこで、investing.comからダウンロードしたデータの中の前述比率を用いて教師データを作ります。
具体的に作成に使用した関数は以下です。
def classify(x):
# 前日比が-0.2%以下ならグループ0
if x <= -0.2:
return 0
# 前日比が0.2%<x<0.2%ならグループ1
elif -0.2 < x < 0.2:
return 1
# 前日比が0.2%以上ならグループ2
elif 0.2 <= x:
return 2
なぜ前日比を-0.2%と0.2%で区切ったのかと言いますと、
・100 (円/ドル) × 0.002 = 0.2(円/ドル) = 20pipsで、この値はレートが動いたかどうかを判断する値として適切だと考えたから。
・前日比を-0.2%と0.2%で三つのグループに区切ることでデータがほぼほぼ当分されるから。(下の図)
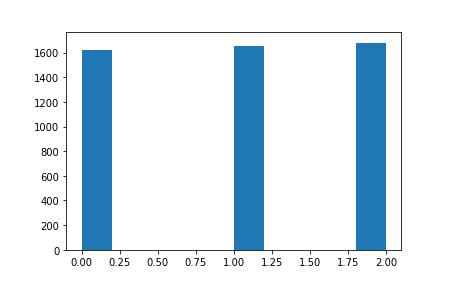
左からグループ0、グループ1、グループ2のデータの数です。ほぼほぼ等分されています。教師データのクラスが等分されていることはランダムフォレストを用いる上でとても大切です。(もちろんクラスが等分されていなくてもできますが、重みづけをする必要があります。詳しくはこちらの方の記事がわかりやすいです。)
以上に注意して教師データを作ります。
df["前日比_float"] = df["前日比%"].apply(lambda x: float(x.replace("%", "")))
# 前日比%の分類の仕方。できるだけ各クラスのサンプルが等しいようにわける
def classify(x):
if x <= -0.2:
return 0
elif -0.2 < x < 0.2:
return 1
elif 0.2 <= x:
return 2
df["前日比_classified"] = df["前日比_float"].apply(lambda x: classify(x))
# 教師にしたいデータを一日ずつずらす(意味を考えればわかると思います)
df_y = df["前日比_classified"].shift()
4. 特徴量と教師データ完成!
少しだけ処理を行います。例えばSMA5を使って特徴量を算出した場合、最初の4日は値がNaNになってしまいます。(5日平均を計算するには最低5日分のデータが要るので)
このように、特徴量データの最初の方にNaNが含まれているので、取り除いてやります。
df_xy = pd.concat([df_feature, df_y], axis=1)
df_xy = df_xy.dropna(how="any")
これで前処理完了です。なお今回はランダムフォレストを用いるので正規化/標準化は必要ありません。
5. モデル学習!
あとは学習するのみです。
ランダムフォレストのパラメータを色々と変えて実験してみると面白いかも...
ランダムフォレストのハイパーパラメータはこちらの記事がわかりやすいです。
あと、ハイパーパラメータはoptunaを使って最適化しました。
optunaを使う際、objective関数は最小化したいものをreturnで返すように設定することに注意しましょう。
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
import optuna
X_train, X_test, Y_train, Y_test = train_test_split(df_xy[["SMA5/current", "SMA20/current","RSI","MACD","BBANDS+2σ","BBANDS-2σ"]],df_xy["前日比_classified"], train_size=0.8)
def objective(trial):
min_samples_split = trial.suggest_int("min_samples_split", 2,16)
max_leaf_nodes = int(trial.suggest_discrete_uniform("max_leaf_nodes", 4,64,4))
criterion = trial.suggest_categorical("criterion", ["gini", "entropy"])
n_estimators = int(trial.suggest_discrete_uniform("n_estimators", 50,500,50))
max_depth = trial.suggest_int("max_depth", 3,10)
clf = RandomForestClassifier(random_state=1, n_estimators = n_estimators, max_leaf_nodes = max_leaf_nodes, max_depth=max_depth, max_features=None,criterion=criterion,min_samples_split=min_samples_split)
clf.fit(X_train, Y_train)
return 1 - accuracy_score(Y_test, clf.predict(X_test))
study = optuna.create_study()
study.optimize(objective, n_trials=100)
print(1-study.best_value)
print(study.best_params)
ハイパーパラメータが最適化された時のaccuracyは、
0.6335025380710659
三値分類なのでなかなかの成績だと思います。ランダムに選択した場合の約二倍の成績ですね。
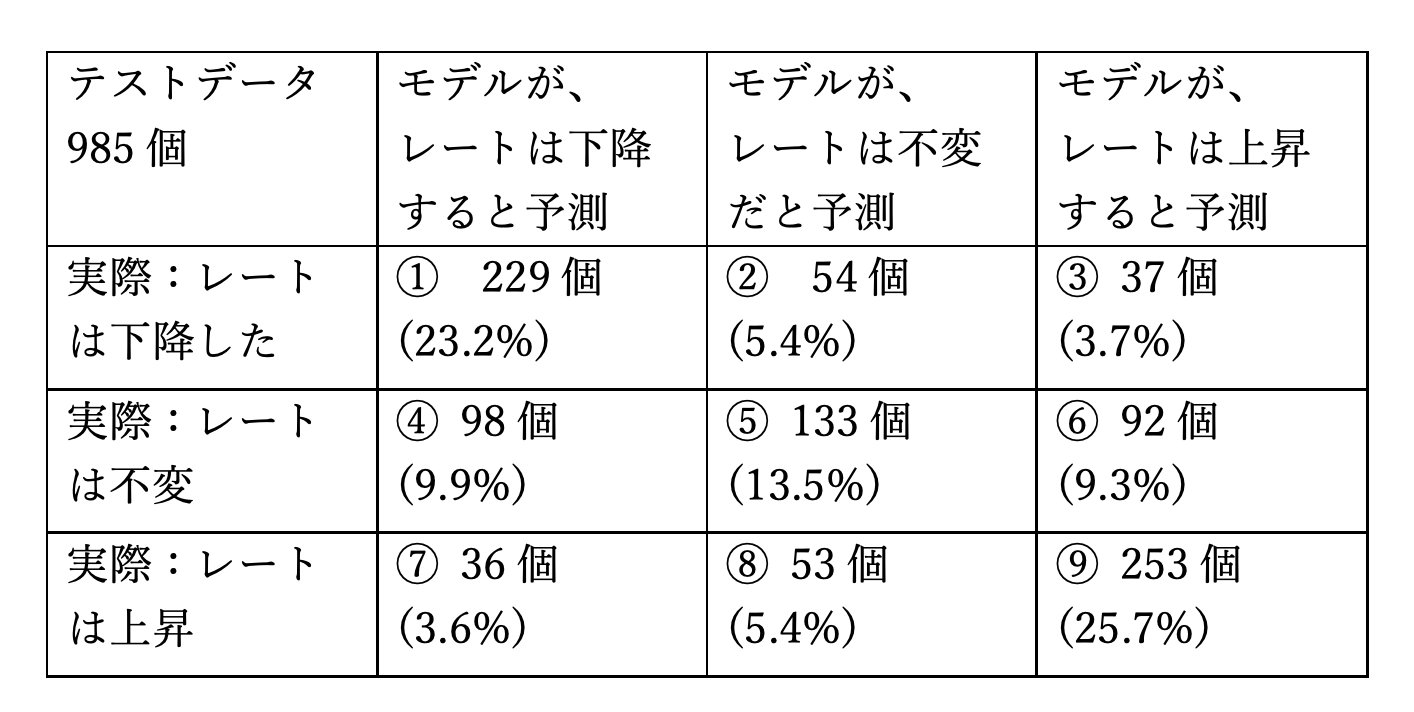
6割の確率で値動きの予想が当たるなら、スプレッド考えても期待値が正になりそう!
Fxで利益を上げるには①と⑨の割合が高いことが望ましいですよね。混同行列を見ると、1+9=48.9%で約半数近くを占めています。また、最も回避したいの は③と⑦のパターンですね(上がると予測したのに実際は下がってしまった、下がると予測したのに実際は上がってしまったというパターン)。これら二つは、③+⑦=7.3%とかなり低い数値になっています。
以上の考察から、今回学習されたモデルは利益を上げることが可能であることがわかります。
また、accuracyが最大となった時のハイパーパラメータは、
{'min_samples_split': 8,
'max_leaf_nodes': 40.0,
'criterion': 'entropy',
'n_estimators': 310.0,
'max_depth': 7}
でした。
ハイパーパラメータとaccuracyの関係は以下のようなものとなりました。
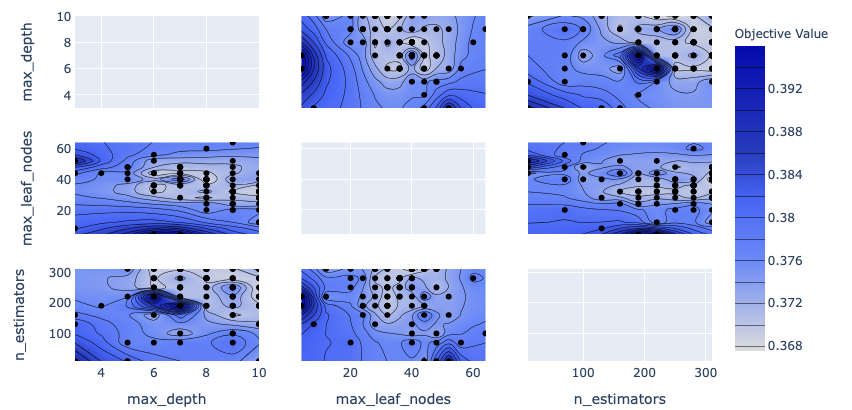
(※obejective_value = 1 - accuracyであることに注意!(optunaの仕様))
上の図の色が薄いところがaccuracyが高くなっているところです。
確かに、max_depthは7付近、max_leaf_nodesは30〜40付近、n_estimatorsは300付近で高いパフォーマンスを出せていることが読み取れます。
追記:さらなる実験
さてここまでは、3値分類してきましたが、レート上昇or下降の二値分類してみましょう。
変更するのは、3.教師データ作成のclassify関数だけです。
def classify(x):
if x <= 0:
return 0
else:
return 1
同じようにモデルを構築し、optunaでハイパーパラメータを最適化してあげると...
accuracy=0.7766497461928934
これで僕も大金持ちですね(白目)!
※投資判断は自己責任です。
このように、データの分割方法を変更するだけではなく、用いるテクニカル指標などもいじってみると面白いかもしれませんね!