フィボナッチ数列とは
自然界の現象によく出現する数列のこと。ひまわりの種の数とかアリの家系図をたどると現れるらしい。発見者はフィボナッチさん。どうやって発見したんだろう。
定義される式は以下のとおり。nをフィボナッチ数列のn番目とすると、
F_{0} = 0
F_{1} = 1
F_{2} = 1
F_{n} = F_{n-1} + F_{n-2} (n \leq 3)
となる。
この数式を眺めると、$F_{n}$の箇所が再帰的にできそうな感じ。再帰的ってことは木構造にすることもできる。
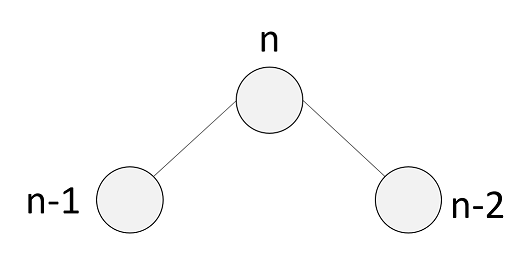
$F_{n} = F_{n-1} + F_{n-2}$を木構造で表現するとこうなる。シンプル。
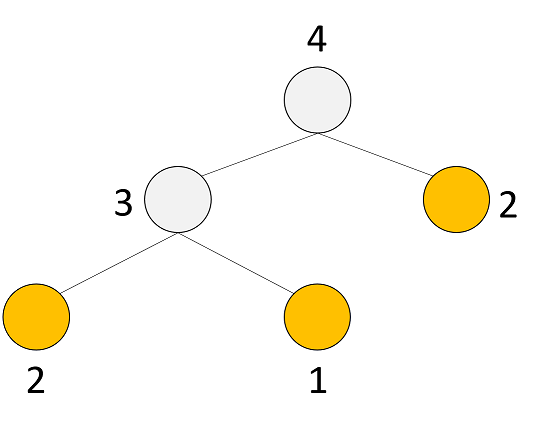
さて、ここで$F_{n}$をn=4に置き換えてみる。
F_{4} = F_{3} + F_{2}
ここで$F_{n} = F_{n-1} + F_{n-2} (n \leq 3)$を思い出してほしい。$(n \leq 3)$の場合、$F_{n}$の式を当てはめることができる。今回、$F_{4}$と$F_{3}$が当てはまる。すでに$F_{4}$は式にしているので、$F_{3}$を当てはめてみる。
F_{3} = F_{2} + F_{1}
これらから、次のような式が導き出せる。
F_{4} = F_{3} + F_{2}
F_{4} = (F_{2} + F_{1}) + F_{2}
プログラミング
で、上の木構造を何とかプログラムに落とし込んでみる。今回出された課題はアセンブラチックにやってくださいとのことだったので、頑張ってみる。今回使用したレジスタはr1からr8まで。とりあえず全部乗っけてみる。なお、実際にアセンブラではないのでこのまんま書いても意味ないのであしからず。
number r8, 0
number r1, 10
number r2, 1
number r3, 2
number r4, 3
number r5, 0
number r6, 0
call r7, fib
call r7, put
exit
fib: add r8, r8, r2
store r8, r1
lt r5, r1, r4
jmpf r5, lnode
move r1, r2
jmp end
lnode: sub r1, r1, r2
lt r5, r1, r4
jmpf r5, lnext
add r6, r6, r2
load r8, r1
sub r8, r8, r2
rnode: sub r1, r1, r3
lt r5, r1, r4
jmpf r5, lnext
add r6, r6, r2
jmpf r8, end
load r8, r1
sub r8, r8, r2
jmp rnode
lnext: add r8, r8, r2
store r8, r1
jmp lnode
end: move r1, r6
ret r7
準備、呼び出し、表示、終了
まず、r8はスタックポインタらしいので、スタックの先頭を指定する。
number r8, 0
r1をnとして考えると、今回は10項めのフィボナッチ数が欲しいので、10を指定する。また、r1は回答が代入されるレジスタとしても使用する。
number r1, 10
r2, r3は$F_{n-1}, F_{n-2}$の-1と-2のところなので、1と2を指定する。
number r2, 1
number r3, 2
r4は条件分岐のための条件として、$n < 3$を指定したいので、3を指定する。
number r4, 3
r5は真偽値が入るので、とりあえず0(偽)で。
number r5, 0
r6は、$F_{n} (0 \leq n, n \leq 2)$の個数を数えるレジスタなので、0を指定。
number r6, 0
そんでもってfibラベルを呼び出して計算を開始する。(この計算は後ほど)
call r7, fib
計算終了後、r1に格納された値を出力する。
call r7, put
おれは幸せなexitをして終了
exit
レジスタをまとめると
-
r1
-
$F_{n}$のnのところ。また、回答を保持して出力するレジスタ。
-
r2
-
$F_{n-1}$の1のところ。また、インクリメント担当。
-
r3
-
$F_{n-2}$の2のところ。それだけ。
-
r4
-
$(3 \leq n)$の3の部分。
-
r5
-
みんな大好きtrue,falseを司るレジスタ。1がtrueで0がfalse。
-
r6
-
計算中の解を保持しておくレジスタ。
-
r7
-
返り番地のいれるとこ。
-
r8
-
スタックポインタ。初期値は0。
fibラベル
こっから計算を始める。
まず、初めのノードの値(r1)をスタックする。
スタックポインタの値を1にして
add r8, r8, r2
1番地にスタックする。
store r8, r1
r1が3よりも小さい場合、真偽値を1(真)にする。
lt r5, r1, r4
真偽値が0だったら左側の子ノードへ移動する。
jmpf r5, lnode
1だったら、3よりも小さいので、r6を1にしてendに飛ぶ
move r6, r2
jmp end
lnodeラベル
ここは左側のノードの処理。(アイじゃなくてエルだよ)
ここは、$F_{n} = F_{n-1} + F_{n-2}$でいうところの$F_{n-1}$のところ
n(r1)-1をする。
sub r1, r1, r2
n-1が3よりも小さいなら、真偽値を1にする。
lt r5, r1, r4
真偽値が0ならn >= 3なので、左側の子ノードへ移動する前処理を行う。
jmpf r5, lnext
真偽値が1ならn < 3なので、$F_{2}$または$F_{1}$より、r6に1を加算。
add r6, r6, r2
親ノードへ移動。
load r8, r1
スタックポインタを減らす。
sub r8, r8, r2
この後ろにrnodeラベルがあるから、自動的に右の子ノードへ移動する。
rnode
右側のノードの処理。
$F_{n-2}$のところ
n-2をする。
sub r1, r1, r3
n-2 < 3 = 1
lt r5, r1, r4
真偽値が0(n-2 >= 3)の場合、左側の子ノードへ移動する前処理をする。
jmpf r5, lnext
真偽値が1(n-2 < 3)の場合、r6に1を加算する。
add r6, r6, r2
右側ノードが終端であり、スタックポインタがない場合、木の探索が完了したので、endラベルへ移動する。
jmpf r8, end
探索が終了していない場合、親ノードへ戻る。
load r8, r1
sub r8, r8, r2
今回は左側から探索しているので、右側ノードが終端である場合、親ノードの左側子ノードも探索済みなので、右側の子ノードへ移動する。
jmp rnode
lnext
現在のノードから子ノードへ移動するとき、現在のノードの値(n = r1)を保持する処理。ここに来る処理の場合、左側の子ノードへ移動することが保証されている。
スタックポインタを一つ増やして現在のノード値をスタックする。
add r8, r8, r2
store r8, r1
左側の子ノードへ移動する。
jmp lnode
endラベル
ここは探索が終了したときに来る。計算した解をr1へ移動させる処理をさせて、呼び出し元に帰っている。
move r1, r6
ret r7
おわり
急いで書いたから図とか入れれなかったけど機会があったら入れてみたい。でもまあこの通りに書いていったらできると思う。(追伸:課題提出するんならマルコピは勘弁な。多少はがんばれ)
あと、課題4だけど
number r1, 10
のところを
call c7, get
に変えるだけで対応可能です。お試しあれ。