モートン順序と四分木で画像分割

平面分割アルゴリズムの模写のようなことをJavaScriptでやりたいと思い、その過程で学んだことを記録します。

平面分割の条件は上記の記事に習って輝度の標準偏差が一定の値を超えたかどうか、とします。これはざっくり言えば、色の変化が激しい部分ほど細かく分割されることを意味します。

条件を満たせばそのレベルのノードに空間内のRGBの平均を保存します。条件を満たしていない場合は、さらに空間を分割して探索レベルを深くします。

大まかな流れは以下のようになります。

1. 画像データを取得
2. 全ピクセルのRGB情報に所属する空間のモートン番号を付ける
3. 必要なレベルまでデータを探索し線形4分木に色を登録
4. 生成した線形4分木から画像を描画

via http://linkalink.jp/enok/?p=229

画像データを取得

ピクセルの情報を取得するため、Canvas APIを使用します。getImageData関数で画像データを取得できます。

some2DContext.getImageData().data;
//このようなRGBA形式の1次元配列が得られる
[r0, g0, b0, a0, r1, g1, b1, a1, ... ]

モートン順序

モートン順序（Morton Order）はゲームで衝突判定の高速化などに使われるようですが、これが非常によくできており、4分木ノードのインデックスと親子関係を簡潔に表現することができます。

例えば、ルート空間（レベル0、未分割）を4分割した空間（レベル1）は以下のように表現できます。

y\x	0	1
0	$0_{\ (00)_2}$	$1_{\ (01)_2}$
1	$2_{\ (10)_2}$	$3_{\ (11)_2}$

ここで、インデックスの順序を追うと、Zの形（0→1→2→3）になっています。そのため、Z-Orderとも呼ばれるようです。また、インデックスの2進数表記を併記してありますが、ここで、2bitの1桁目がx軸の位置、2桁目がy軸の位置になっていることが重要な意味を持ちます。

レベル1の空間をそれぞれ4分割した空間（レベル2）はどうなるでしょうか。

下のように、親空間をZ型の順序で4分割していきます。

	$\,\,\,Z\,\,\,$	$\,\,\,Z\,\,\,$
	$\,\,\,Z\,\,\,$	$\,\,\,Z\,\,\,$

第2レベルは以下のように表現されます。

y\x	0	1	2	3
0	$0_{\ (00)_2}$	$1_{\ (01)_2}$	$4_{\ (100)_2}$	$5_{\ (101)_2}$
1	$2_{\ (10)_2}$	$3_{\ (11)_2}$	$6_{\ (110)_2}$	$7_{\ (111)_2}$
2	$8_{\ (1000)_2}$	$9_{\ (1001)_2}$	$12_{\ (1100)_2}$	$13_{\ (1101)_2}$
3	$10_{\ (1010)_2}$	$11_{\ (1011)_2}$	$14_{\ (1110)_2}$	$15_{\ (1111)_2}$

インデックスを取り出して2bitずつ分けると、最初の2bitは親空間でのインデックス、次の2bitが自分の空間でのインデックスとなっています。

\begin{eqnarray*}
3&=&(0011)_2\\
&=&(00)_2(11)_2\\
&=&(0)_{10}\rightarrow(3)_{10}\\[1em]
13&=&(1101)_2\\
&=&(11)_2(01)_2\\
&=&(3)_{10}\rightarrow(1)_{10}\\[1em]
\end{eqnarray*}

また、インデックスの奇数ビット、偶数ビットを取り出すと全体での座標がわかります。

\begin{eqnarray*}
9&=&(1001)_2\\
&=&(10)_2(01)_2
\end{eqnarray*}

奇数桁のみ取り出す

\begin{eqnarray*}
x&=&(0)_2(1)_2\\
&=&(01)_2\\
&=&1
\end{eqnarray*}

偶数桁のみ取り出す

\begin{eqnarray*}
y&=&(1)_2(0)_2\\
&=&(10)_2\\
&=&2
\end{eqnarray*}

この性質は木が深くなっても変わりません。

モートン順序を使用することで、4分木がどれだけ深くても所属空間の情報を保持した状態で線形化することが可能になります。またいつでも所属する空間を復元することができます。

そこで、線形4分木への登録の下準備として、得られたピクセルすべてに最大探索レベルでのモートン番号を付与します。

例えば、600x600ピクセルの画像をレベル3まで探索すると1辺は$2^3$で分割されますので、75x75ピクセルが1つの空間に登録されることになります。

via http://marupeke296.com/COL_2D_No8_QuadTree.html

線形4分木にデータを登録する

得られたピクセルリストから線形4分木へデータを登録していきます。

線形4分木のポインタ$P$に登録するピクセルデータを、探索レベル$L$、モートン番号$M$を使用して取り出します。

ここで、線形4分木のオフセット（各レベルの開始ポインタ）$O$は、探索レベルを$L$とすると、

O=\frac{4^L-1}{4-1}\\

モートン番号$M$は、

M=P-O

$P$	0	1	2	3	4	5	6	7	8	9	10	...
$L$	0	1	1	1	1	2	2	2	2	2	2	...
$O$	0	1	1	1	1	5	5	5	5	5	5
$M$	0	0	1	2	3	0	1	2	3	4	5	...

これで、ポインタからモートン番号を得ることができました。

ピクセルの所属判定

例えば最大探索レベル3の4分木でモートン番号$45$の親の所属空間は

\begin{eqnarray*}
45\gg2(3-2)&=&(101101)_2\gg2\\
&=&(1011)_2\\
&=&11
\end{eqnarray*}

一般に最大探索レベル$L_{MAX}$で、モートン番号$M$のレベル$L$の親空間$M'$は

M'=M\gg2(L_{MAX}-L)

この親空間に所属するピクセルだけを取り出します。

レベル1／モートン番号3の空間であればすべてのピクセルから$(11)_2$に所属するピクセル$(11XXXX\dots)_2$を取り出します。

※ここでは$\ll,\gg$をビットシフト演算を示す記号として使っています。

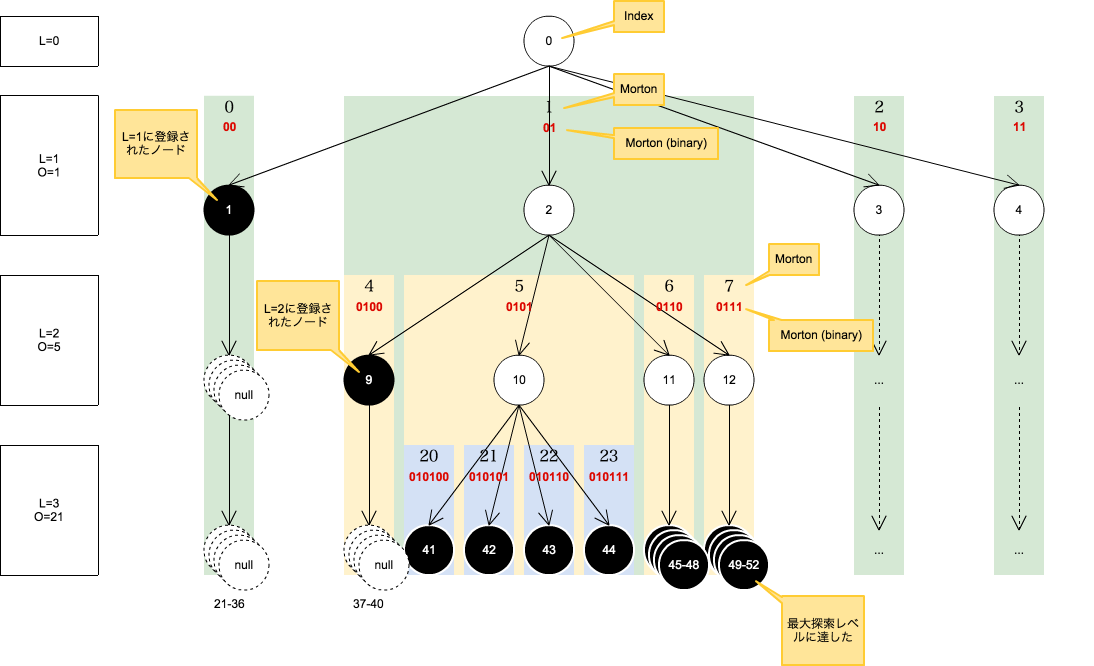
ノードの登録

枝とデータを1対1にするため親ノードから登録状況を判別できるようにします。そのためにデータノード、ダミーノード、nullの3種類のノードを用意します。

• 親がダミーノードなら、ダミーノードまたはデータノードを登録できます（未探索）。
• 親がデータノードならnullしか登録できません（探索済み）。
• 親がnullならnullしか登録できません（探索済み）。

ダミーノードから開始（ルート空間）、条件を満たしてデータノードが登録された枝は探索済み（登録不可）、そうでない枝は未探索（登録可能）とします。データが登録されると以降の子空間はnullとなり、登録不可となります。

	探索済み	未探索
条件を満たす	null	データノード
条件を満たさない	null	ダミーノード

次レベルのオフセットに達したら探索レベルを上げます。最大レベルに達したら条件に関わらず登録します。

下図に4分木の概要を示します。

データの描画

こうしてできあがった4分木を走査してデータを描画します。nullノードとダミーノードは無視します。

この画像の場合、最大探索レベル8、標準偏差の閾値は18です。

私はアルゴリズムに特段詳しいわけではないので、ちゃんと説明になっているかわからないのですが、モートン順序の有用性と美しさが伝われば幸いです。