NumPyroで階層ベイズをやってみる

ここでは、NumPyroで階層ベイズを行う方法について紹介する。NumPyroはJAXをバックエンドにする確率的プログラミング言語であり、推論が爆速であることで知られる。

次のようなソーシャルメディアのデータ(ぶっちゃけtwitter)について分析することを想定したい。
ユーザーの行動データが複数あり、ユーザーが他のユーザーをフォローするなどコミュニティが形成される場合、コミュニティレベル、ユーザーレベル、ユーザーの行動レベルと3つの階層が作られることが考えられる。独立変数はユーザーが閲覧したテキストの表現であり、従属変数はユーザーが書いたテキストの表現であるとする(例えば、辞書や教師あり学習でポジネガ分類をした)。

独立変数: x1, x2、 x1とx2の交互作用
従属変数: y(ある行動をするかどうか0, 1)
階層構造: ユーザーレベル、コミュニティレベル

その場合、コードは下記のようになる。

def model(N, User_N,  User, Community_N ,Community2User, x1, x2, y = None):
    a_0 = numpyro.sample("a_0", dist.Normal(0, 10))
    sigma_a = numpyro.sample("sigma", dist.HalfNormal(5))
    b1_0 = numpyro.sample("b1_0", dist.Normal(0, 10))
    sigma_b1 = numpyro.sample("sigma_b1", dist.HalfNormal(5))
    b2_0 = numpyro.sample("b2_0", dist.Normal(0, 10))
    sigma_b2 = numpyro.sample("sigma_b2", dist.HalfNormal(5))
    b_interaction_0 = numpyro.sample("b_interaction_0", dist.Normal(0, 10))
    sigma_b_interaction = numpyro.sample("sigma_b_interaction", dist.HalfNormal(5))
    sigma_a_community = numpyro.sample("sigma_a_community", dist.HalfNormal(5))
    sigma_b1_community = numpyro.sample("sigma_b1_community", dist.HalfNormal(5))
    sigma_b2_community = numpyro.sample("sigma_b2_community", dist.HalfNormal(5))
    sigma_b_interaction_community = numpyro.sample("sigma_b_interaction_community", dist.HalfNormal(5))

    with numpyro.plate("Communitiy_N", size=Community_N):
        a_community = numpyro.sample("a_community", dist.Normal(a_0, sigma_a))
        b1_community  = numpyro.sample("b1_community", dist.Normal(b1_0, sigma_b1))
        b2_community  = numpyro.sample("b2_community", dist.Normal(b2_0, sigma_b2))
        b_interaction_community  = numpyro.sample("b_interaction_community", dist.Normal(b_interaction_0, sigma_b_interaction))
    
    with numpyro.plate("User_N", size=User_N):
        a = numpyro.sample("a", dist.Normal(a_community[Community2User], sigma_a_community))
        b1  = numpyro.sample("b1", dist.Normal(b1_community[Community2User], sigma_b1_community))
        b2  = numpyro.sample("b2", dist.Normal(b2_community[Community2User], sigma_b2_community))
        b_interaction  = numpyro.sample("b_interaction", dist.Normal(b_interaction_community[Community2User], sigma_b_interaction_community))
    q = sigmoid(a[User] + b1[User]*x1 +  b2[User]*x2 +  b_interaction[User]*x1*x2)   

    with numpyro.plate("N", size = N):
        y_pred = numpyro.sample("y_pred", dist.Bernoulli(q), obs=y)

事前分布の選び方はGelmanの記事を参考にすればいい。下記の記事では5つのレベルの事前分布について書いている。

• 一様分布(推奨されない)
• 非常に曖昧な事前分布: normal(0, 1e6)(推奨されない)
• 弱情報事前分布: normal(0, 10)
• 一般的な弱事前情報事前分布: normal(0.4, 0.2)
• 特定の情報事前分布

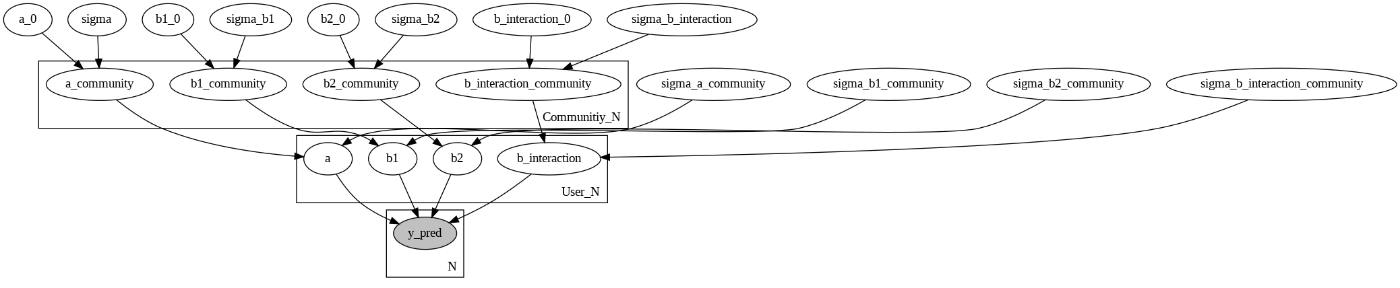
グラフィカルモデルの描画

NumPyroの利点として、グラフィカルモデルを描画できることが挙げられる。

numpyro.render_model(model, model_args=(N, User_N,  User, Community_N ,Community2User, x1, x2, y = None), render_params=True, filename="model.png")

MCMC

事後分布を求めるため、MCMCを行う。NumPyroはPyroのMCMC100倍早いらしい。

kernel = numpyro.infer.NUTS(model)
mcmc = numpyro.infer.MCMC(kernel, num_samples=2000, num_warmup=300, num_chains=4, chain_method="parallel")
mcmc.run(jax.random.PRNGKey(0), N, User_N,  User, Community_N ,Community2User, x1, x2, y)

変分推論

データ量が多い、モデルが複雑であるという場合は、変分推論を使う。

guide = infer.autoguide.AutoDiagonalNormal(model)
optimizer = numpyro.optim.Adam(step_size=0.0005)
svi = SVI(model, guide, optimizer, loss=Trace_ELBO())
svi_result = svi.run(random.PRNGKey(0), 2000, N, User_N,  User, Community_N ,Community2User, x1, x2, y)
params = svi_result.params

num_samples = 1000
dist_posterior = Predictive(model=guide, params=params, num_samples=num_samples)
samples_posterior = dist_posterior(random.PRNGKey(1))
samples_posterior