AD変換するときの雑音の考え方

#はじめに
電子回路の設計なんかをしているとセンサーのアナログ信号をデジタルデータに変換する必要に迫られる事は多いと思います。AD変換して得られるデータの精度は言い換えれば、取得したい情報にどれくらいの雑音が加わるかと言えるでしょう（直線性とかの問題はここでは省略します）。
というわけでAD変換における雑音について説明します。

#誤差は雑音

-2から+2までの振幅を持つ適当なアナログ信号を量子化してみた図になります。

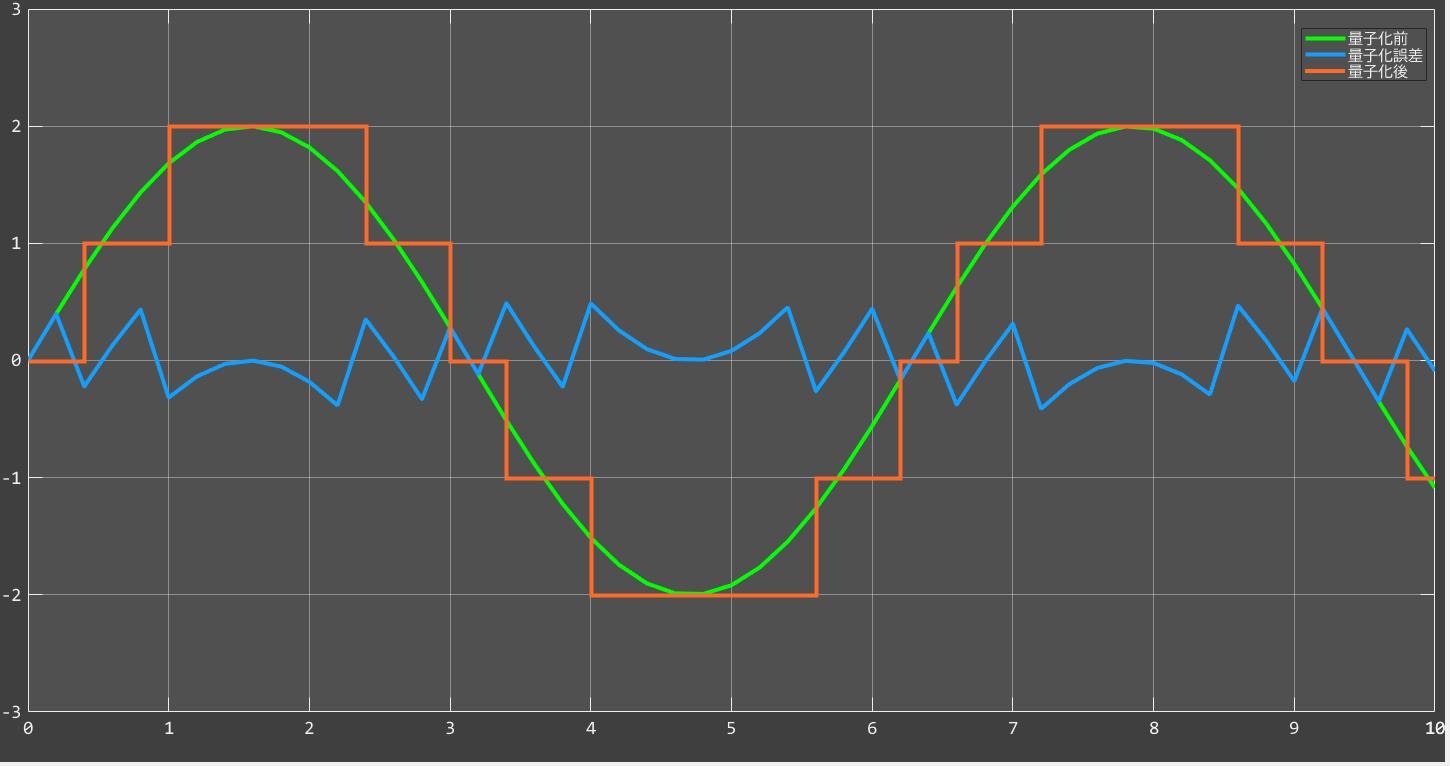
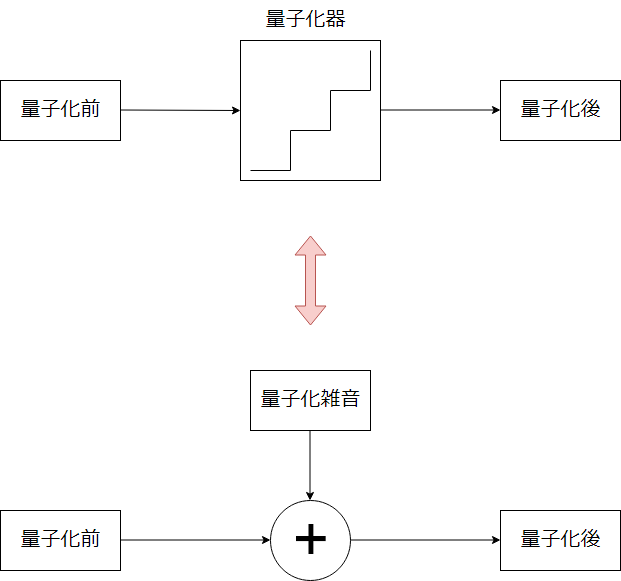
量子化の前後では誤差が生まれます。
これは言い換えれば、量子化とは元の信号に量子化誤差(量子化雑音)を加える行為であると考えられます。

量子化雑音は本来は入力信号に相関性を持つのですが、現実として入力信号に無相関であり、振幅、周波数帯域共に均一に分布して白色雑音（ホワイトノイズ）と同じものであると見なすことができます¹。

ADCの最小分解能をLSBと呼ぶことにします。量子化雑音はLSB/2から-LSB/2までで均一に分布していると考えられます。

確率密度関数を積分することによって量子化雑音の実効値は

V_{QNrms} = \frac{LSB}{\sqrt{12}}

となります¹²。
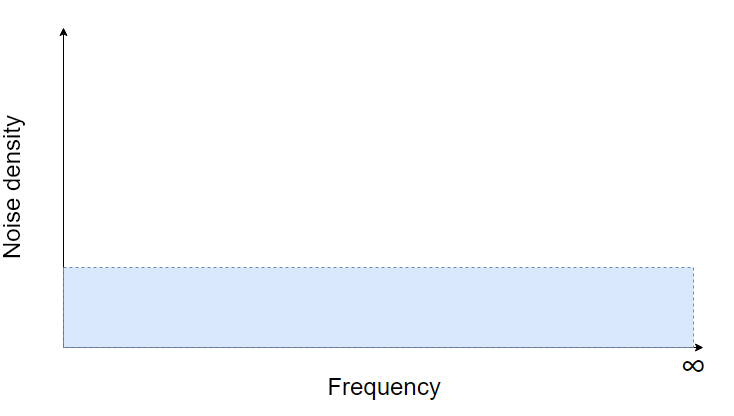
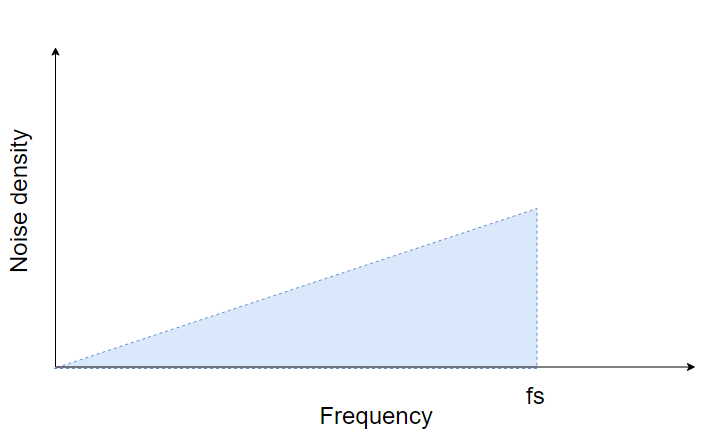
また、量子化雑音は0から∞の周波数まで均一に分布していると考えられるので周波数特性は以下のようになります。

しかしながら現実のAD変換はサンプリング周波数Fsは有限の値をとり、サンプリング定理によってFs/2より大きな周波数帯域は正しく変換されません。それではいったい何が起きるのでしょうか。

サンプリング定理より、サンプリング周波数の半分であるFs/2よりも上の帯域では折返し（エイリアシング）が発生するので、Fs/2までの帯域に∞までの帯域の量子化雑音が全て折り返されます。つまりFs/2までのノイズの積分は無限大までの量子化雑音の積分値と同じとみなすことができます。このため雑音の振幅は$\frac{LSB}{\sqrt{12}}$のまま変わらないと考えることができます。

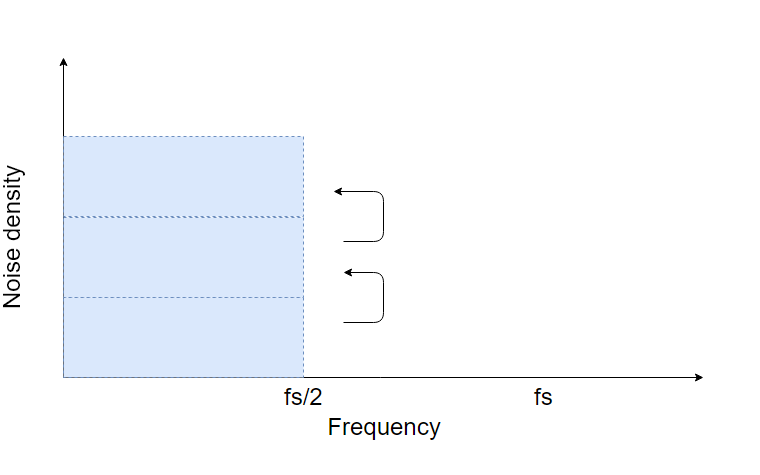
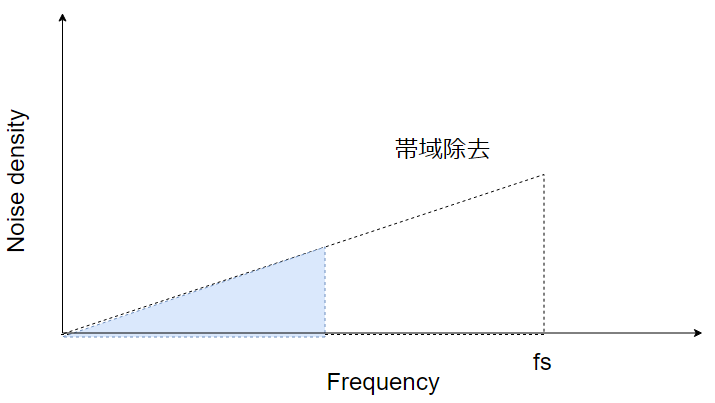
サンプリング周波数を大きくする(オーバーサンプリング)と、周波数当たりの雑音密度が低減します。しかし当然ながらこれだけでは雑音の振幅は変わりません。

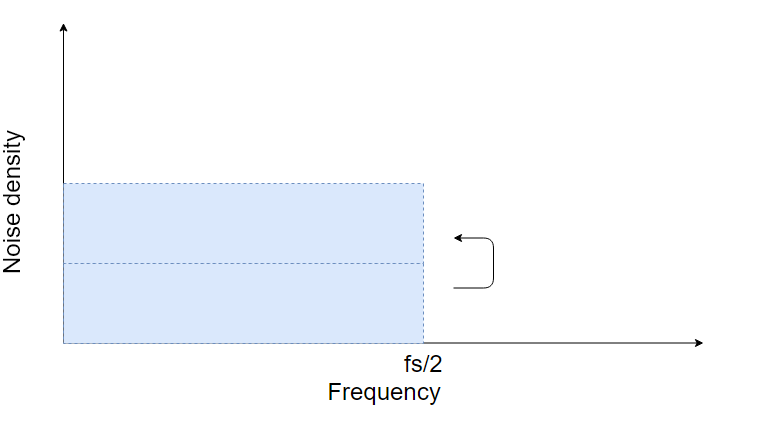
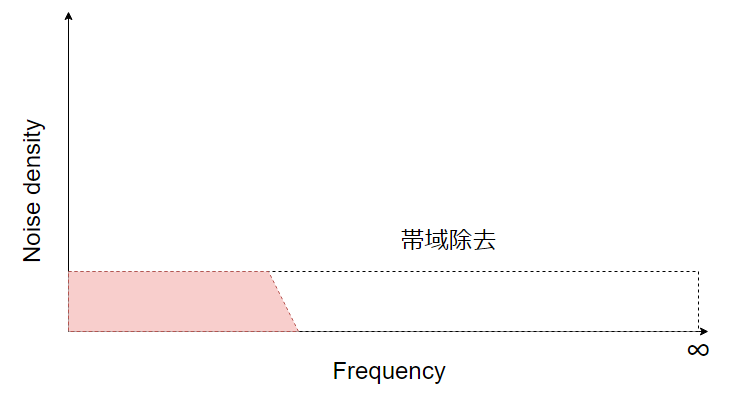
量子化された(量子化雑音が加わった)後に、デジタルフィルタで不要な帯域を除去してしまいます。

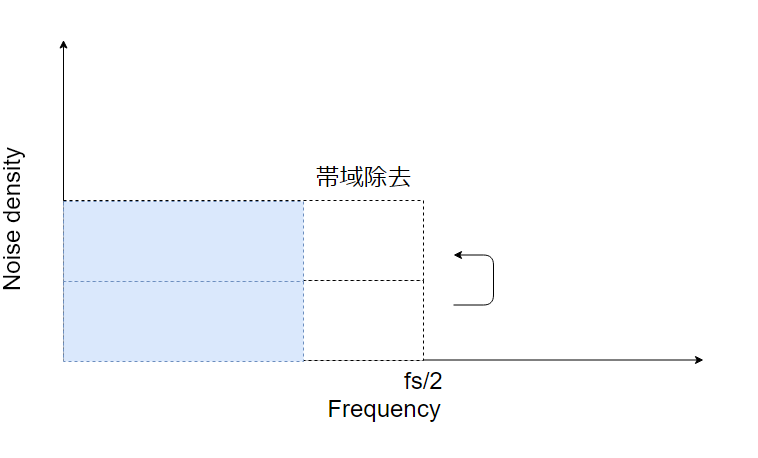
雑音の総量(振幅)が減少することが分かります。

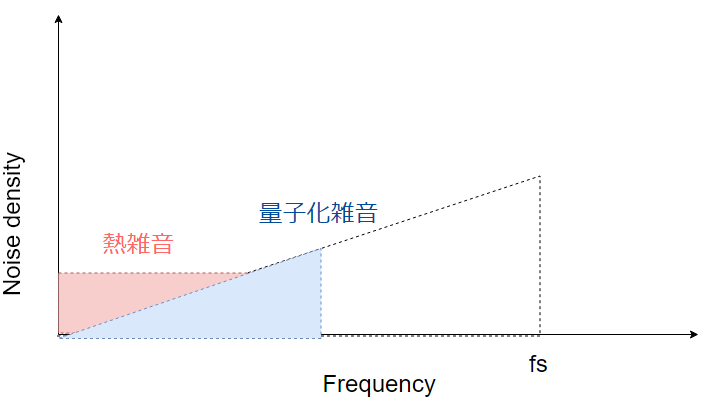
#量子化雑音と熱雑音の違い

電子回路において避けられない雑音の代表として熱雑音があります。量子化雑音と熱雑音は混同してしまいがちですが、違いはあるのでしょうか。

ここでは詳しく解説しませんが、抵抗Rの両端で発生する雑音電圧密度はボルツマン定数kと温度Tを用いて以下の式で表されます³。

e_{R} = \sqrt{4kTR} \; (V/\sqrt{Hz})

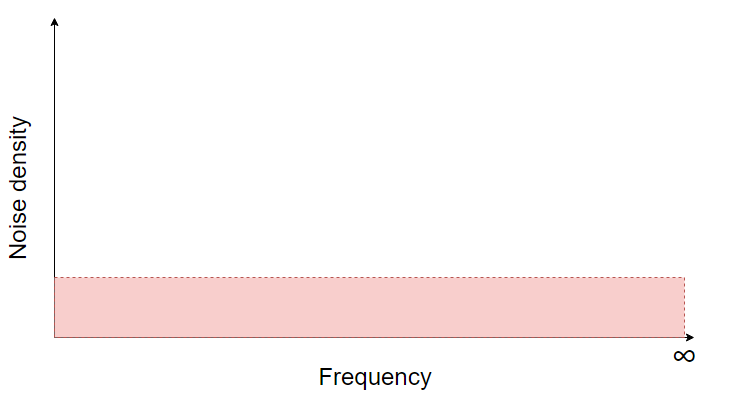
ここからわかるように抵抗両端の熱雑音は周波数帯域で均一の値をとります。

周波数軸上でのスペクトラムを比較すると量子化雑音と熱雑音は見分けることができません。
しかしながら、この二つの雑音は根源が異なります。
熱エネルギーに起因する熱雑音は全ての回路素子で発生し、主にADCの前段の回路で発生するものが支配的になることが多いです。量子化雑音は量子化によってのみ発生します。
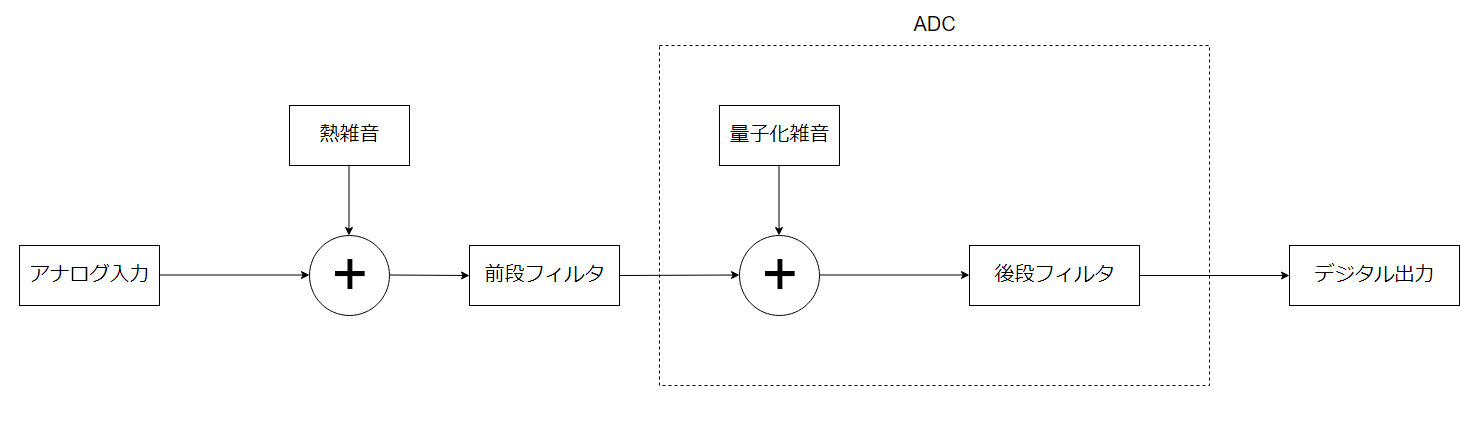
AD変換を行う回路ブロック例を示します。

ADC前段にフィルタを置いて不要な帯域を除去することによって雑音振幅を減らすことができます。

ローパスフィルタのカットオフ周波数がFs/2よりも低い場合、ノイズの折り返しが発生しないのでオーバーサンプリングによって雑音振幅、雑音密度ともに変化しません。

以上をまとめると、量子化雑音を低減するためにはサンプリング周波数を上げてオーバーサンプリングして後段のデジタルフィルタで帯域削減が有効です。一方で抵抗の熱雑音を低減するためには前段のフィルタで帯域削減することが有効です。
デジタル出力には両方の雑音が含まれたデータが出力されるので、どちらか一方の雑音を極端に低減させたとしてももう一方が大きければ低雑音の出力が得られないことになります。

#ノイズシェーピング

デルタシグマ方式のADCでは量子化雑音をノイズシェーピングして高精度を実現しています⁴。

これまで量子化雑音は全ての周波数帯域に均一に分布していると説明してきましたが、デルタシグマADCでは積分器とフィードバックを利用することによって量子化雑音の周波数帯域の分布を変化させます。このとき量子化雑音の振幅の分布は変化していないことに注意が必要です。

ノイズシェーピングはオーバーサンプリング、デジタルフィルタと組み合わせたときに大きな威力を発揮します。測定したい信号が含まれず、雑音が多く含まれる帯域を削ることによって高い信号‐雑音比(SNR)が得られます。

この特性からデルタシグマADCは測定対象の周波数帯域が低ければ低いほど他のADC方式に比べて有利な精度が得られます。
気を付けるべきなのはノイズシェーピングは量子化雑音にのみ有効な技術です。ノイズシェーピングやオーバーサンプリングによって量子化雑音を限りなく0に近づけたとしても回路の熱雑音が支配的となるので完全に雑音の無いデジタル出力が得られるわけではありません。

#参考文献
Shanthi Pavan, Richard Schreier, Gabor C. Temes, Understanding Delta-Sigma Data Converters, IEEE Press Series on Microelectronic Systems

1. https://www.analog.com/media/jp/training-seminars/tutorials/mt-001_jp.pdf ↩ ↩²

2. https://classes.engineering.wustl.edu/ese488/Lectures/Lecture5a_QNoise.pdf ↩

3. https://kats.issp.u-tokyo.ac.jp/kats/circuit3/doc/note/note10.pdf ↩

4. https://www.analog.com/media/jp/technical-documentation/application-notes/AN-283_jp.pdf ↩